Линейные и квадратные уравнения

Линейное уравнение, записанное в общем виде, можно рассматривать как уравнение с параметрами: ах = b, где х – неизвестное, а, b – параметры. Для этого уравнения особым или контрольным значением параметра является то, при котором обращается в нуль коэффициент при неизвестном.

При решении линейного уравнения с параметром рассматриваются случаи, когда параметр равен своему особому значению и отличен от него.

Особым значением параметра а является значение а = 0.

1. Если а ≠ 0 , то при любой паре параметров а и b оно имеет единственное решение х = .

2. Если а = 0, то уравнение принимает вид: 0 х = b. В этом случае значение b = 0 является особым значением параметра b. 

2.1. При b ≠ 0 уравнение решений не имеет.

2.2. При b = 0 уравнение примет вид: 0 х = 0. Решением данного уравнения является любое действительное число.

Пример. Решить уравнение

2а(а — 2) х = а — 2.    (1)

Решение. Здесь контрольными будут те значения параметра, при которых коэффициент при х обращается в 0. Такими значениями являются а=0 и а=2. При этих значениях а невозможно деление обеих частей уравнения на коэффициент при х. В то же время при значениях параметра а≠0, а≠2 это деление возможно. Таким образом, целесообразно множество всех действительных значений параметра разбить на подмножества

A₁={0}, А₂={2} и А₃= {а≠0, а≠2}

и решить уравнение (1) на каждом из этих подмножеств, т. е. решить уравнение (1) как семейство уравнений, получающихся из него при следующих значениях параметра:

1) а=0 ; 2) а=2 ; 3) а≠0, а≠2.

Рассмотрим эти случаи.

1) При а=0уравнение (1) принимает вид 0 х = - 2. Это уравнение не имеет корней.

2) При а=2уравнение (1) принимает вид 0 х=0. Корнем этого уравнения является любое действительное число.                                                                              

3) При а≠0, а≠2 из уравнения (1) получаем, х = ,

откуда х = .

0твет: 1) Если а=0,то корней нет;

              2)если а=2, то х – любое действительное число;                                          

               3) если а≠0, а≠2 , то х =  .

Пример.Решить уравнение

(а — 1) х²+2 (2а+1) х+(4а+3) =0; (2)

Решение.  В данном случае контрольным является значение a=1. Дело в том, что при a=1 уравнение (2) является линейным, а при а≠ 1 оно квадратное (в этом и состоит качественное изменение уравнения). Значит, целесообразно рассмотреть уравнение (2) как семейство уравнений, получающихся из него при следующих значениях параметра: 1) а = l; 2) а≠1.

Рассмотрим эти случаи.

1) При a=1 уравнение (2) примет вид 6х+7=0. Из этого

    уравнения находим х = - .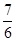

2) Из множества значений параметра а ≠ 1 выделим те значения, при которых дискриминант уравнения (2) обращается в 0.

Дело в том, что если дискриминант D=0 при а=а_о, то при переходе значения D через точку а_о дискриминант может изменить знак (например, при а<а_о D< 0, а при а>а_о D>0). Вместе с этим при переходе через точку а_о меняется и число действительных корней квадратного уравнения (в нашем примере при а<а_о корней нет, так как D< 0, а при а>а_о D>0 уравнение имеет два корня). Значит, можно говорить о качественном изменении уравнения. Поэтому значения параметра, при которых обращается в 0 дискриминант квадратного уравнения, также относят к контрольным значениям.

Составим дискриминант уравнения (2):

=(2а+ l)² — (а — 1) (4а+3). После упрощений получаем = 5а+4.

Из уравнения = 0 находим а = - — второе контрольное значение параметра а. При

этом если а <- , то D <0; если a≥- , то D≥0, a ≠ 1.

Таким образом, осталось решить уравнение (2) в случае, когда а <-   и в случае, когда { a≥- , a ≠ 1 }.

Если а <- , то уравнение (2) не имеет действительных корней; если же

{ a≥- , a ≠ 1 }, то находим

Ответ: 1) если  а <- , то корней нет; 

              2) если  а = 1, то х = - ;

              3) если a≥- , a ≠ 1, то       .