 |
Главная |
Показательные и логарифмические неравенства с параметрами
|
из
5.00
|
Пример. Найти все значения параметра  , при которых неравенство
, при которых неравенство

выполняется для всех действительных значений  .
.
Решение. Исходное неравенство

равносильно следующей совокупности двух систем:


|
|

В системе (1) параметр  , поэтому коэффициент
, поэтому коэффициент  , стоящий при
, стоящий при  в левой части последнего неравенства, положителен, следовательно, последнее неравенство системы (1) равносильно неравенству
в левой части последнего неравенства, положителен, следовательно, последнее неравенство системы (1) равносильно неравенству

которое не может выполняться при всех действительных значениях  при любом фиксированном значении параметра
при любом фиксированном значении параметра  . Таким образом, система (1) не дает искомых значений параметра.
. Таким образом, система (1) не дает искомых значений параметра.
В системе
 (2)
(2)
из первого неравенства (  ) так же, как и раньше, вытекает, что
) так же, как и раньше, вытекает, что  , следовательно, второе неравенство равносильно неравенству
, следовательно, второе неравенство равносильно неравенству
 ,
,
которое, очевидно, выполняется для всех действительных  тогда и только тогда, когда
тогда и только тогда, когда
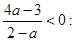

С учетом того, что  , получаем
, получаем 
Ответ: 
Производная и ее применения
Пример.Найти все значения параметра  , при которых функция
, при которых функция

имеет хотя бы один экстремум строго между числами  и
и  .
.
Решение. Для вычисления экстремумов функции  найдем её производную:
найдем её производную:
 откуда следует, что в точках экстремума, то есть при
откуда следует, что в точках экстремума, то есть при  , значение параметра
, значение параметра  , так как
, так как  . Поэтому интервал
. Поэтому интервал  , на котором, согласно условию задачи, надо искать экстремум, целиком расположен справа от точки 0.
, на котором, согласно условию задачи, надо искать экстремум, целиком расположен справа от точки 0.
Дальнейшее решение задачи изложим двумя способами.
I- ый способ. Рассмотрим квадратный трехчлен  с абсциссой вершины
с абсциссой вершины  и дискриминантом
и дискриминантом  , положительность которого следует из того, что
, положительность которого следует из того, что 
Если абсцисса  вершины параболы, являющейся графиком функции
вершины параболы, являющейся графиком функции  , расположена левее интервала
, расположена левее интервала  , то есть величина
, то есть величина  , то значения
, то значения  и
и  должны быть разных знаков, причем
должны быть разных знаков, причем  - отрицательно:
- отрицательно:

откуда следует, что 
Если  лежит строго между
лежит строго между  и
и  , то либо
, то либо  , либо
, либо  должно быть положительно:
должно быть положительно:

Если 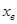 лежит правее интервала
лежит правее интервала  , то есть
, то есть  , то значения
, то значения 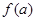 и
и  должны быть разных знаков, причем
должны быть разных знаков, причем  - положительно:
- положительно:

Объединяя найденные значения параметра  в рассмотренных трех случаях
в рассмотренных трех случаях  , получает ответ:
, получает ответ:  .
.
II – й способ.

Как мы уже получили ранее, в точках экстремума, то есть при  имеем
имеем  . В плоскости
. В плоскости  нарисуем график функции
нарисуем график функции  . Точки экстремума будем искать на интервале
. Точки экстремума будем искать на интервале  , то есть при
, то есть при  что соответствует внутренним точкам острого угла, ограниченного прямыми
что соответствует внутренним точкам острого угла, ограниченного прямыми  и
и  , и находящегося в первой четверти. Найдем точки пересечения прямых
, и находящегося в первой четверти. Найдем точки пересечения прямых  и
и  с параболой
с параболой  . Решая квадратные уравнения, получаем:
. Решая квадратные уравнения, получаем:


Так как производная  при
при  и
и  при
при  , то исходная функция
, то исходная функция  является возрастающей в области
является возрастающей в области  , расположенной ниже параболы
, расположенной ниже параболы  , и убывающей в области, расположенной выше этой параболы; в точках параболы функция
, и убывающей в области, расположенной выше этой параболы; в точках параболы функция  имеет экстремум (в силу того, что выполнено достаточное условие экстремума – смена знака производной).
имеет экстремум (в силу того, что выполнено достаточное условие экстремума – смена знака производной).
Левая ветвь параболы  пересекается с прямыми
пересекается с прямыми  и
и  в точках
в точках  и
и  соответственно. Все точки параболы, расположенные строго между этими точками пересечения, отвечают точкам экстремума функции
соответственно. Все точки параболы, расположенные строго между этими точками пересечения, отвечают точкам экстремума функции  , соответствующим искомым значениям параметра
, соответствующим искомым значениям параметра  :
:  (проекция на ось
(проекция на ось  указанного участка левой ветви параболы
указанного участка левой ветви параболы  ).
).
Правая ветвь параболы  пересекается с прямыми
пересекается с прямыми  и
и  в точках
в точках  и
и  соответственно. Все точки параболы, расположенные строго между этими точками пересечения, отвечают точкам экстремума функции
соответственно. Все точки параболы, расположенные строго между этими точками пересечения, отвечают точкам экстремума функции  , соответствующим искомым значениям параметра
, соответствующим искомым значениям параметра  :
:  (проекция на ось
(проекция на ось  указанного участка правой ветви параболы
указанного участка правой ветви параболы  ).
).
Объединяя найденные выше интервалы  и
и  значений параметра
значений параметра  , получаем ответ.
, получаем ответ.
Ответ:  .
.
Заключение
Введение элективного курса «Решение задач с параметрами» необходимо учащимся в наше время как при подготовке к ЕГЭ, так и к вступительным экзаменам в ВУЗы. Владение приемами решения задач с параметрами можно считать критерием знаний основных разделов школьной математики.
Даже если бы эти задачи не предлагались на выпускных и вступительных экзаменах, то все равно в школьной математике задачам с параметрами должно уделяться большое внимание. В этом автор данного реферата глубоко убеждена: ведь известно, какую роль играют данные задачи в формировании логического мышления и математической культуры у школьников. Поэтому учащиеся, владеющие методами решения задач с параметрами, успешно справляются (и опыт это подтверждает) с другими задачами. Решение задач, уравнений с параметрами открывает перед учащимися значительное число эвристических приемов общего характера, ценных для математического развития личности, применяемых в исследованиях и на любом другом математическом материале.
При решении задач с параметрами одновременно активно реализуются основные методические принципы:
принцип параллельности – следует постоянно держать в поле зрения несколько тем, постепенно продвигаясь по ним вперед и вглубь;
принцип вариативности – рассматриваются различные приемы и методы решения с различных точек зрения: стандартность и оригинальность, объем вычислительной и исследовательской работы;
принцип самоконтроля – невозможность подстроиться под ответ вынуждает делать регулярный и систематический анализ своих ошибок и неудач;
принцип регулярности – увлеченные математикой дети с удовольствием дома индивидуально исследуют задачи, т. е. занятия математикой становятся регулярными, а не от случая к случаю на уроках.
Разработанный элективный курс может быть использован учителями математики при подготовке к ЕГЭ, вступительным экзаменам в ВУЗы, на занятиях математического кружка. В нем систематизирован теоретический и дидактический материал, отвечающий принципу последовательного нарастания сложности.
|
из
5.00
|
Обсуждение в статье: Показательные и логарифмические неравенства с параметрами |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

