Изучение приложения производной в курсе школьной математики

 

Понятие непрерывной функции

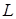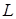Остановимся на понятии непрерывной функции: функция  стремится к числу  при  ( ), если разность  сколь угодно мала, т.е.  становится меньше любого фиксированного  при уменьшении . Нахождение числа  по функции  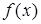называется предельным переходом.

Этим названием уже пользовались, давая определения производной. Предельный переход – новая операция для нахождения неизвестных величин. Так, например, функция 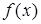 называется непрерывной в точке x₀, если  при  или

 

= .

 

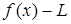В учебнике "Алгебры и начала анализа 10-11 класс" формулируются правила новой операции:

1) Если функция  непрерывна в точке , то  при

2) Если функция  имеет производную в точке , то:  при

3) Пусть ,  при.  Тогда при :

 

а)  ;

б) ;

в) , если .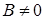

 

Метод интервалов

Приложения производной начинаются с рассмотрения приложения непрерывной функции: "Если на интервале 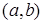 функция  непрерывна и не обращается в нуль, то на этом интервале она сохраняет постоянный знак! " Эта теорема применяется в решении неравенств методом интервалов. В более "сильных" классах можно заменить нахождение знака данной функции на каждом из интервалов проведением кривой знаков ", которая берет свое начало в правом верхнем углу, если знак коэффициента при старшей степени  положителен, и в правом нижнем углу в противном случае (вспомнить аналогию с расположением ветвей параболы для функции ).

Например: решить неравенство

 

 

 

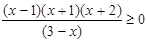
Ответ: .

Исследование свойств функции с помощью производной

Рассматриваются примеры разрывной функции: 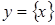, непрерывной, но не дифференцируемой в точке, функции .

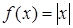При исследовании свойств функции с помощью производной опираются на такие известные теоремы математического анализа, как теоремы Лагранжа, Ферма и Вейерштрасса. Формула Лагранжа как иллюстрация геометрического смысла производной приводится в пункте 19 "Касательная к графику функции" и, немного позже, с ее применением формулируется достаточные признаки возрастания и убывания функции:

 

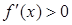
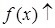; , т.к. ,

 

где 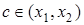 - формула Лагранжа.

Методическая схема изучения достаточных признаков возрастания и убывания функции:

· поставить учебную проблему;

· подвести учащихся к формулировке признака с помощью геометрической иллюстрации;

· сформулировать признак, привести краткую запись его условия и заключения.

· привести доказательство признака с помощью формулы Лагранжа;

· закрепить доказательство путем выделения в нем составляющих шагов.

Например, подведение учащихся к формулировке признака возрастания функции конкретно- индуктивным методом можно осуществить следующим образом, обращаясь к учащимся, учитель говорит: "Можно ли охарактеризовать поведение функции с помощью производной? ". Рассмотрим рисунок

 

 

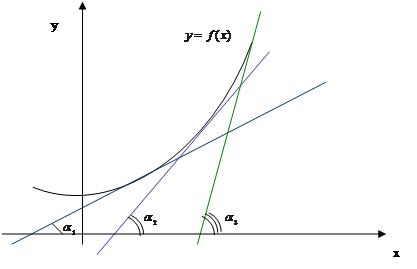
Как ведет себя функция ?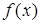

Здесь приведен график функции, которая в каждой точке промежутка (a,b) имеет положительную производную. Что можно сказать о поведении функции на данном промежутке? Высказывается предположение, что функция возрастает. Справедливо ли это? Для ответа на этот вопрос приводятся примеры других функций, производная которых положительна на некотором промежутке:

, ;

, .

 

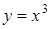
На основе индуктивного обобщения рассмотренных примеров формулируется соответствующий признак.

 

Заключение

 

Т.о. методическая схема изучения достаточных признаков возрастания и убывания функции:

· поставить учебную проблему;

· подвести учащихся к формулировке признака с помощью геометрической иллюстрации;

· сформулировать признак, привести краткую запись его условия и заключения.

· привести доказательство признака с помощью формулы Лагранжа;

· закрепить доказательство путем выделения в нем составляющих шагов.

 

Литература

 

1. К.О. Ананченко "Общая методика преподавания математики в школе", Мн., "Унiверсiтэцкае",1997г.

2.Н.М.Рогановский "Методика преподавания в средней школе", Мн., "Высшая школа", 1990г.

3.Г.Фройденталь "Математика как педагогическая задача",М., "Просвещение", 1998г.

4.Н.Н. "Математическая лаборатория", М., "Просвещение", 1997г.

5.Ю.М.Колягин "Методика преподавания математики в средней школе", М., "Просвещение", 1999г.

6.А.А.Столяр "Логические проблемы преподавания математики", Мн., "Высшая школа", 2000г.