 |
Главная |
Процедура решения задачи
|
из
5.00
|
1. Используя алгоритм градиентного спуска с постоянным шагом, найти точку х k в которой выполнен по крайней мере один из критериев окончания расчетов.
2. Провести анализ точки х k с целью установить, является ли точка хк найденным приближением решения задачи. Процедура анализа определяется наличием у функции f (х) непрерывных вторых производных. Если  , то следует провести проверку выполнения достаточных условий минимума: матрица Гессе
, то следует провести проверку выполнения достаточных условий минимума: матрица Гессе 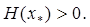 Если
Если  то точка х k есть найденное приближение искомой точки х*. Если
то точка х k есть найденное приближение искомой точки х*. Если  , то следует провести проверку функции f (х) на выпуклость в Q-окрестности точки х k, используя критерий выпуклости для функций
, то следует провести проверку функции f (х) на выпуклость в Q-окрестности точки х k, используя критерий выпуклости для функций  : функция f ( x ) выпукла (строго выпукла) в том и только в том случае, если
: функция f ( x ) выпукла (строго выпукла) в том и только в том случае, если  . Если функция f ( x ) выпукла (строго выпукла), то х k есть найденное приближение точки х*.
. Если функция f ( x ) выпукла (строго выпукла), то х k есть найденное приближение точки х*.
Определение: Матрицей Гессе Н(х) дважды непрерывно дифференцируемой в точке х функции f ( x ) называется матрица частных производных второго порядка, вычисленной в данной точке:
 ,
,
где 
Определители 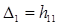 ,
,  , …,
, …,  называются угловыми минорами.
называются угловыми минорами.
Пример 1.1. Найти локальный минимум функции

□ I. Определение точки х k, в которой выполнен по крайней мере один из критериев окончания расчетов.
1. Зададим х0,  ,
,  , М: х0 = (0,5; 1)T,
, М: х0 = (0,5; 1)T,  = 0,1;
= 0,1;  = 0,15 ; М = 10. Найдем градиент функции в произвольной точке
= 0,15 ; М = 10. Найдем градиент функции в произвольной точке 
2. Положим к = 0.
30. Вычислим  :
:  = (3;2,5)Т.
= (3;2,5)Т.
40. Вычислим  :
:  = 3,9 > 0,1. Переходим к шагу 5.
= 3,9 > 0,1. Переходим к шагу 5.
50. Проверим условие  : k = 0 < 10 = M . Переходим к шагу 6.
: k = 0 < 10 = M . Переходим к шагу 6.
60. Зададим  = 0,5 .
= 0,5 .
70. Вычислим х1: х1 = (0,5; 1)T -0,5(3; 2,5)T = (-1; -0,25)T; f (х1) = 2,31.
80. Сравним f (х1) с f (х0) = 2. Имеем f (х1) > f (х0). Вывод: условие  для k = 0 не выполняется. Зададим
для k = 0 не выполняется. Зададим  = 0,25, переходим к повторению шагов 7, 8.
= 0,25, переходим к повторению шагов 7, 8.
701. Вычислим х1: х1 = (0,5; 1)T-0,25(3; 2,5)T = (-0,25; 0,375)T; f (х1) = 0,171.
801. Сравним f (х1) и f (х0). Вывод: f ( x 1 ) < f ( x 0 ). Переходим к шагу 9.
90. Вычислим  и
и  :
:
 =0,976 > 0,15;
=0,976 > 0,15; 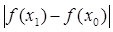 = 1,829 > 0,15.
= 1,829 > 0,15.
Вывод: полагаем k =1 и переходим к шагу 3.
31. Вычислим  :
:  = (-0,625;0,51)Т.
= (-0,625;0,51)Т.
41. Вычислим  :
:  = 0,81. Переходим к шагу 5.
= 0,81. Переходим к шагу 5.
51. Проверим условие  : k = 1 < 10 = M. Переходим к шагу 6.
: k = 1 < 10 = M. Переходим к шагу 6.
61. Зададим  = 0,25.
= 0,25.
71. Вычислим х2: х2 = (-0,25; 0,375)T - 0,25 (-0,625; 0,5)T = (-0,094; 0,25)T; f (х2) = 0,056.
81. Сравним f (х2) с f (х1). Вывод: f (х2) < f (х1). Переходим к шагу 9.
91. Вычислим  и
и  :
:
 = 0,2 > 0,15;
= 0,2 > 0,15;  = 0,115 < 0,15.
= 0,115 < 0,15.
Вывод: полагаем k = 2 и переходим к шагу 3.
32. Вычислим  :
:  = (-0,126; 0,406)Т.
= (-0,126; 0,406)Т.
42. Вычислим  :
:  = 0,425 > 0,1. Переходим к шагу 5.
= 0,425 > 0,1. Переходим к шагу 5.
52. Проверим условие  : k = 2 < 10 = М, переходим к шагу 6.
: k = 2 < 10 = М, переходим к шагу 6.
62. Зададим  =0,25.
=0,25.
72. Вычислим х3: х3 = (-0,094; 0,25)T -0,25(-0,126; 0,406)T = (-0,063;0,15)T ; f (х3) = 0,021.
82. Сравним f (х3) и f (х2) . Вывод: f (х3) < f (х2).Переходим к шагу 9.
92. Вычислим 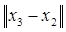 и
и  :
:
 = 0,105 < 0,15;
= 0,105 < 0,15;  = 0,035 < 0,15.
= 0,035 < 0,15.
Вывод: полагаем k =3 и переходим к шагу 3.
33. Вычислим  :
:  = (-0,102; 0,237)T.
= (-0,102; 0,237)T.
43. Вычислим  :
:  = 0,257 > 0,1 . Переходим к шагу 5.
= 0,257 > 0,1 . Переходим к шагу 5.
53. Проверим условие  : k = 3<10 = М, переходим к шагу 6.
: k = 3<10 = М, переходим к шагу 6.
63. Зададим  = 0,25.
= 0,25.
73. Вычислим х4: х4 = (-0,063; 0,15)T - 0,25(-0,102; 0,237)T = (-0,038; 0,091)Т; f (х4) = 0,0076.
83. Сравним f (х4) и f (х3): f (х4) < f (х3).
93. Вычислим 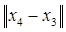 и
и  :
:
 = 0,064 < 0,15;
= 0,064 < 0,15;  = 0,015 < 0,15.
= 0,015 < 0,15.
Условия  ,
, 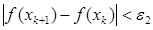 выполнены при k = 2,3. Расчет окончен. Найдена точка х4 = (-0,038; 0,091)Т; f ( x 4 ) = 0,0076.
выполнены при k = 2,3. Расчет окончен. Найдена точка х4 = (-0,038; 0,091)Т; f ( x 4 ) = 0,0076.
На рис. 3 полученные точки соединены пунктирной линией.
II. Анализ точки х4.
Функция  является дважды дифференцируемой, поэтому проведем проверку достаточных условий минимума в точке х4. Для этого проанализируем матрицу Гессе
является дважды дифференцируемой, поэтому проведем проверку достаточных условий минимума в точке х4. Для этого проанализируем матрицу Гессе  .
.

Рис. 3
Матрица постоянна и является положительно определенной (т.е. H > 0) , так как оба ее угловых минора 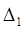 = 4 и
= 4 и  = 7 положительны. Следовательно, точка х4=(-0,038; 0,091)T есть найденное приближение точки локального минимума х* = (0,0)T, а значение f ( x 4 ) =0,0076 есть найденное приближение значения f ( x * ) =0. Заметим, что условие H > 0, есть одновременно условие строгой выпуклости функции
= 7 положительны. Следовательно, точка х4=(-0,038; 0,091)T есть найденное приближение точки локального минимума х* = (0,0)T, а значение f ( x 4 ) =0,0076 есть найденное приближение значения f ( x * ) =0. Заметим, что условие H > 0, есть одновременно условие строгой выпуклости функции  . Следовательно, х4 = (-0,038; 0,091)T, f ( x 4 ) =0,0076 есть найденные приближения точки глобального минимума f ( x ) и ее наименьшего значения на R 2. ■
. Следовательно, х4 = (-0,038; 0,091)T, f ( x 4 ) =0,0076 есть найденные приближения точки глобального минимума f ( x ) и ее наименьшего значения на R 2. ■
|
из
5.00
|
Обсуждение в статье: Процедура решения задачи |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

