 |
Главная |
Процедура решения задачи
|
из
5.00
|
1. Используя алгоритм Ньютона, найти точку х k, в которой выполняется по крайней мере один критерий окончания расчета.
2. Так как  , то осуществить проверку выполнения достаточных
, то осуществить проверку выполнения достаточных
условий минимума  > 0. Если условие выполнено, то точка х k может рассматриваться как найденное приближение точки минимума х*. Проверку выполнения достаточных условий минимума можно заменить проверкой функции f ( x ) на выпуклость.
> 0. Если условие выполнено, то точка х k может рассматриваться как найденное приближение точки минимума х*. Проверку выполнения достаточных условий минимума можно заменить проверкой функции f ( x ) на выпуклость.
Пример 2.1. Найти локальный минимум функции
 .
.
□ I. Определение точки х k, в которой выполняется по крайней мере один критерий окончания расчетов.
1. Зададим х0, 
 М: х0 = (0,5; 1)Т,
М: х0 = (0,5; 1)Т, 
 ; М=10. Найдем градиент функции в произвольной точке
; М=10. Найдем градиент функции в произвольной точке  и матрицу Гессе
и матрицу Гессе  .
.
2. Положим k = 0.
30. Вычислим  :
:  = (3; 2,5)Т.
= (3; 2,5)Т.
40. Проверим выполнение условия  :
:  = 3,9 > 0,1.
= 3,9 > 0,1.
Переходим к шагу 5.
50. Проверим выполнение условия  : k = 0 <10. Переходим к шагу 6.
: k = 0 <10. Переходим к шагу 6.
60. Вычислим  :
: 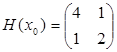 .
.
70. Вычислим  :
:  .
.
80. Проверим выполнение условия  >0. Так как
>0. Так как 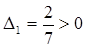 ,
,  , то согласно критерию Сильвестра
, то согласно критерию Сильвестра  > 0.
> 0.
90. Определим  .
.
100. Вычислим  .
.
110. Проверим выполнение условий  ,
,  :
:
 = 1,12 > 0,15;
= 1,12 > 0,15;  = 2>0,15.
= 2>0,15.
Полагаем k = 1, переходим к шагу 3.
31. Вычислим  :
:  = (0,0)T.
= (0,0)T.
41. Проверим выполнение условия  :
:  = 0 <0,1. Расчет окончен. Заметим, что в точке х1 выполняется необходимое условие первого порядка, поэтому она является стационарной точкой.
= 0 <0,1. Расчет окончен. Заметим, что в точке х1 выполняется необходимое условие первого порядка, поэтому она является стационарной точкой.
II. Анализ точки х1.
Функция  является строго выпуклой, так как ее матрица вторых производных
является строго выпуклой, так как ее матрица вторых производных  в силу того, что
в силу того, что  ,
,  .
.
Найденная точка х1 =(0,0)T есть точка локального и одновременно глобального минимума f (х).

Рис. 9
На рис. 9 траектория спуска изображена сплошной линией. ■
Метод Ньютона-Рафсона
Стратегия поиска
Стратегия метода Ньютона-Рафсона [Newton-Raphson] состоит в построении последовательности точек {х k}, k = 0,1,..., таких, что  k = 0,1,.... Точки последовательности вычисляются по правилу
k = 0,1,.... Точки последовательности вычисляются по правилу
 (7)
(7)
где х0 задается пользователем; величина шага 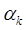 определяется из условия
определяется из условия
 . (8)
. (8)
Задача (7.5) может решаться либо аналитически с использованием необходимого условия минимума  с последующей проверкой достаточного условия
с последующей проверкой достаточного условия 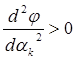 , либо численно как задача
, либо численно как задача
 (9)
(9)
где интервал [a , b]задается пользователем.
Если функция  достаточно сложна, то возможна ее замена полиномом
достаточно сложна, то возможна ее замена полиномом  второй или третьей степени и тогда шаг
второй или третьей степени и тогда шаг 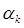 может быть определен из условия
может быть определен из условия  при выполнении условия
при выполнении условия  .
.
При численном решении задачи определения величины шага степень близости найденного значения 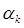 к оптимальному значению
к оптимальному значению  , удовлетворяющему условиям
, удовлетворяющему условиям  ,
, 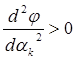 , зависит от задания интервала [a , b]и точности методов одномерной минимизации.
, зависит от задания интервала [a , b]и точности методов одномерной минимизации.
Построение последовательности {х k} заканчивается в точке х k, для которой  , где
, где  - заданное число, или при
- заданное число, или при  (М - предельное число итераций), или при двукратном одновременном выполнении двух неравенств
(М - предельное число итераций), или при двукратном одновременном выполнении двух неравенств  ,
, 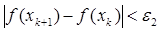 , где
, где  - малое положительное число.
- малое положительное число.
Вопрос о том, может ли точка х k рассматриваться как найденное приближение искомой точки минимума, решается путем проведения дополнительного исследования, которое описано ниже.
Сходимость
Утверждение. Пусть функция f ( x ) дважды непрерывно дифференцируема и сильно выпукла на Rn , а ее матрица Гессе Н(х) удовлетворяет условию Липшица

 .
.
Тогда последовательность {х k } сходится независимо от выбора начальной тонки х0 к точке минимума х* с квадратичной скоростью
 ,
,
где т - оценка наименьшего собственного значения матрицы.
Замечание. Сходимость к точке минимума метода Ньютона-Рафсона гарантируется независимо от выбора начального приближения лишь для сильно выпуклых функций. Поэтому при практическом использовании метода Ньютона-Рафсона следует:
а) анализировать матрицу Гессе  на выполнение условия
на выполнение условия  >0, k= 0,1,..., и заменять формулу
>0, k= 0,1,..., и заменять формулу  на формулу метода градиентного спуска
на формулу метода градиентного спуска  в случае его невыполнения;
в случае его невыполнения;
б) производить анализ точки х k с целью выяснения, является ли она найденным приближением искомой точки х*.
|
из
5.00
|
Обсуждение в статье: Процедура решения задачи |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

