Сокращенные и тупиковые дизъюнктивные нормальные формы

Известно [4], что всякую булеву функцию можно записать, причем единственным образом, в ДНФ, то есть в виде дизъюнкции элементарных конъюнкций (суммы произведений). В связи с этим можно ставить вопрос об отыскании для заданной функций такой ДНФ, которая была бы наиболее простой по сравнению с ее другими ДНФ.

ДНФ называется минимальной, если она содержит по сравнению с другими эквивалентными ей формами минимальное количество букв (при подсчете учитывается каждое вхождение буквы в формулу).

В простейших случаях минимизацию функции можно осуществить, выписав все ДНФ для этой функции и выбрав, из них минимальную. Однако такой примитивный метод очень трудоемок, и мы рассмотрим ниже более оптимальные способы решения этой задачи.

Элементарную конъюнкцию φ_к назовем импликантой булевой функции f, если не существует такого двоичного набора переменных, при котором функция φ_к принимает значение 1, а функция f – значение 0, то ecть φ_k Ú f = f.

Для того чтобы проверить является ли заданная элементарная конъюнкция импликантой функции f, следует всем переменным, которые входят в эту конъюнкцию без знака отрицания, придать значение 1, а тем переменным, которые входят с отрицанием – значение 0. Тогда элементарная конъюнкция будет иметь истинностное значение 1. После этого следует, проверить, принимает ли функция f значение 1 при любых значениях остальных переменных. В дальнейшем для упрощения записибулевых функций знаки коньюнкции будем заменять знаками умножения или просто опускать.

Пример 4. Проверить, являются ли одночлены  и импликантами булевой функции

.

Решение. Полагая в первом случае Х₁ = 1, X₂ = 1, имеем φ₁ = l и φ₂ = l и

,

следовательно, φ₂ – импликанта заданной функции.

Во втором случае полагаем X₁ = 0, X₂ = l. Тогда

φ₂ = 1, а ,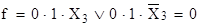

следовательно, φ₂ не является импликантой функции f.

Справедливы следующие утверждения:

1. Если  импликанты булевой функции f, то  и  также являются ее импликантами.

2. Если функция  есть импликанта функции f, то функции  также являются импликантами функции f.

Элементарная конъюнкция, входящая в ДНФ булевой функции, называется ее простой импликантой, если никакая ее часть не является импликантой этой функции.

Сокращенной ДНФ данной булевой функции называется ее ДНФ, составленная только из простых импликант.

Для приведения булевой функции к сокращенной ДНФ используется, так называемое правило склеивания. Оно заключается в следующем. Логическую сумму двух элементарных конъюнкций, отличающихся только знаком отрицания над одной из переменных, можно заменить одной элементарной конъюнкцией, которая является общей частью рассматриваемых слагаемых, т.е.

.

Например,

Для любой заданной функции сокращенная ДНФ является единственной. Однако онa может быть избыточной вследствие тогo, что некоторые простые импликанты этой суммы покрываются совокупностями других слагаемых. Такие импликанты называют лишними, и они могут быть удалены без нарушения равносильности формул.

Сокращенная ДНФ, из которой удалены все лишние импликанты, называется тупиковой ДНФ

Исключение лишних импликант из сокращенной ДНФ проводится с помощью правила поглощения: дизъюнкцию двух элементарных конъюнкций, из которых одна полностью содержится и другой, можно заменить конъюнкцией, имеющей меньший ранг, например, X Ú XF = X,

.

Правила склеивания, и поглощения легко доказываются с помощью таблиц истинности. Кроме этих правил, при минимизации функции могут быть использованы любые известные равносильности.

Пример 5. Упростить булеву функцию .

Решение. Эта функция содержит только простые импликанты, т. е. является сокращенной Однако она избыточна, так как одночлен Х₁X₂ можно удалить, не разрушая равносильности. После этого получим функцию:

.

Пример 6. Найти минимальную ДНФ для функции

    .

Решение. Склеивая первый и третий одночлены по переменкой Х₂, получим Х₁X₃X₄. Из первого и четвертого, а затем из второго и третьего слагаемых после склеивания получим соответственно X₁X₂X₃,  и т. д. Окончательный список импликант имеет вид

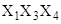
В этом списке имеется два одночлена X₁X₃ и Х₂Х₃Х₄, которые не поглощают других одночленов из этого списка, следовательно, являются простыми импликантами. Поэтому сокращенная ДНФ имеет вид

,

οна же является и минимальной

В общем случае процесс построения минимальных ДНФ может быть охарактеризован следующей схемой.

Рис. 1

Сначала получают сокращенную ДНФ. Далее однозначный процесс переходит в ветвящийся процесс построения всех тупиковых ДНФ и, наконец, из тупиковых ДНФ выделяются минимальные. Самым трудоемким этапом этого процесса является построение тупиковых ДНФ. Его можно немного упростить, заранее удалив часть членов сокращенной ДНФ, не участвующих в построении тупиковых ДНФ и тем самым сократить количество просматриваемых подмножеств

Проблема минимизации является важнейшей для технических приложений логических функций и ей посвящено много работ, в которых предложены различные алгоритмы решения этой задачи. Рассмотрим подробнее один из таких алгоритмов.

3. Алгоритм Квайна иМак-Класки минимизации булевой функции

Этот алгоритм используется наиболее часто, так как он может быть реализован на ЭВМ, и при его применении практически отсутствуют ограничения на число переменных. Минимизацию функции в этом методе рекомендуется выполнить в следующей последовательности.

1. Привести булеву функцию к СДНФ.

2. В СДНФ произвести все возможные склеивания Полученная после этого ДНФ является сокращённой, но среди простых импликант могут оказаться лишние.

3. Перейти от сокращённой ДНФ к минимальной, т.е. исключить лишние импликанты. Для этого рекомендуется воспользоваться импликантой матрицей, в которой каждой строке соответствует простая импликанта, а каждому столбцу – конституента ( элементарная конъюнкция, содержащая все переменные) СДНФ заданной функции Эта матрица заполняется следующим образом под конституентами, в которые входит данная простая импликанта, ставится метка "1" Для нахождения минимального покрытия функции необходимо удалить из таблицы некоторые лишние простые импликанты С этой целью реализуется следующий алгоритм.

1. Выделение ядра Квайна. Если в каком-либо столбце импликантной матрицы имеется только одна 1, то импликанта, находящаяся в соответствующем столбце, не является лишней и должна быть включена в минимальное покрытие функции. Такие импликанты называются существенными, а их совокупность называют ядром Квайна.

Вычёркивая строки, в которых находятся существенные импликанты, и столбцы, покрываемые этими импликантами, получаем матрицу меньших размеров Если в ней имеются столбцы, содержащие по одной 1, то операцию выделения существенных импликант следует повторить.

2 Сжатие по столбцам или строкам. Из матрицы вычёркивается тот столбец, в который полностью входит какой-либо другой столбец и та строка, которая полностью покрывается другой.

После выполнения всех указанных действий в матрице останутся только те простые импликанты, которые входят в минимальное покрытие функции. Соединив эти импликанты и найденные ранее существенные импликанты знаками дизъюнкций, получим минимальную ДНФ заданной функции.

Пример 7 Минимизировать булеву функцию

.

Решение. Функция задана в ДНФ, поэтому займемся сразу отысканием простых импликант, проводя операцию склеивания. Для этого представим каждую элементарную конъюнкцию двоичным набором, ставя на k-ом месте 0, если Х_k входит с отрицанием, 1 – если без отрицания и знак "–", если эта переменная не входит в конъюнкцию Тогда функция примет вид:

.

Разобьем эти наборы на классы, в каждом из которых содержатся наборы с одинаковым числом единиц и расположим ихв порядке возрастания суммы всех чисел набора (рис 2 а)

Для исключения переменных по правилу склеивания сравним все наборы всех смежных классов. Если при этом какая-либо переменная исключается, то в разряд, соответствующий этой переменной, записываем прочерк. Например, двоичные наборы 0100 и 0101 образуют набор 010–. Все полученные наборы опять разбиваем на классы. Объединяем снова наборы из двух смежных классов, причём сравнению подлежат только те, у которых прочерк находится в одном и том же разряде, получаем новый набор импликант (рис. 2 в). Нетрудно убедиться, что дальнейшее объединение наборов невозможно, следовательно, все полученные импликанты – простые.

Построим импликантную матрицу (табл. 3 а). Выделяя столбцы, содержащие по одной единице, находим существенные импликанты, образующие ядро Квайна: 0–0–  –0–0. При этом первая из них является существенной для 0000, 0001, 0100, 0101, а вторая – для 0000, 0010, 1000, 1010. Вычёркивая столбцы с этими конституентами и строки с существенными импликантами, получим табл. 3 б. В этой таблице нет столбцов, содержащих только одну единицу, следовательно существенных импликант в этой таблице нет и ядро Квайна состоит из двух импликант, найденных выше: 0–0– и –0–0.

Переходим к операциям сжатая по строкам и столбцам. Вторая строка табл. 3 б поглощает первую, а четвёртая – третью, поэтому первую и третью строки можно вычеркнуть (табл. 3 в).

В табл. 3 в первый столбец полностью входит в четвёртый, а второй – в третий, После вычеркивания четвертого и третьего столбцов таблица принимает вид 3 г. Из этой таблицы видно, что импликанта 111– является лишней, так как не содержит единиц ни в одном столбце, а две остальные входят в минимальное покрытие. Таким образом, заданная функция имеет четыре простых импликанты: 0–0–,  –0–0, 1––0 и –111. Объединяя их знаком дизъюнкции, получаем минимальную ДНФ в виде

.

Алгоритм Квайна позволяет получать минимальные дизъюнктивные нормальные формы заданных функций Однако в ряде случаев минимальные конъюнктивные нормальные выражения оказываются "меньше" дизъюнктивных, поэтому при решении задач минимизации желательно получить не только дизъюнктивные, но и конъюнктивные нормальные формулы и выбрать из них наименьшее. Методы получения минимальных конъюнктивных выражений двойственны рассмотренным выше методам и мы не будем на них останавливаться.