 |
Главная |
Сокращение мономиальных систем
|
из
5.00
|
Пусть 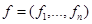 :
: 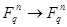 – полиномиальная система, где каждый
– полиномиальная система, где каждый  – моном, такой, что
– моном, такой, что  , где
, где  – неотрицательное целое число. То есть,
– неотрицательное целое число. То есть,  может быть описано матрицей
может быть описано матрицей  . В первую очередь связывается
. В первую очередь связывается 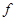 с Булевой мономиальной системой
с Булевой мономиальной системой  и линейной системой
и линейной системой 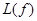 над кольцами
над кольцами  . В работе «Булевы мономиальные системы»
. В работе «Булевы мономиальные системы» 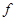 называется системой конечных элементов если все конечные циклы
называется системой конечных элементов если все конечные циклы 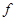 заключаются в фиксированном элементе. Покажем что
заключаются в фиксированном элементе. Покажем что  – конечный элемент системы тогда, и только тогда, когда
– конечный элемент системы тогда, и только тогда, когда  и
и  – системы конечных элементов.
– системы конечных элементов.
Определение 1.2.1.
Для  , мы определим базис
, мы определим базис  , обозначенный supp ( u ), равный
, обозначенный supp ( u ), равный  , где
, где

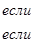
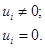
Мономиальная система 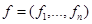 порождает Булеву мономиальную систему
порождает Булеву мономиальную систему  на
на  с параметрами
с параметрами  , где
, где 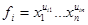 и v = supp ( u ).
и v = supp ( u ).
Лемма 1.2.1.
 - коммутативная диаграмма.
- коммутативная диаграмма.
Доказательство.
Это прямо доказывается тем что supp ( f ( u ))= f ( supp ( u )).
Так как  на множестве всех
на множестве всех  таких, что supp ( u )= u, появляется следующие прямые следствия.
таких, что supp ( u )= u, появляется следующие прямые следствия.
Следствие 1.2.1.
Фазовое пространство  – подграф фазового пространства
– подграф фазового пространства  .
.
Следствие 1.2.2.
Предположим что 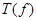 – система конечных элементов. Если
– система конечных элементов. Если  – цикл в фазовом пространстве
– цикл в фазовом пространстве 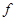 , тогда
, тогда  для всех
для всех  .
.
Пример 1.2.1.
Пусть 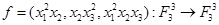 .
.
 - состоит из всех возможных наборов длины 3 из трёх элементов: 0, 1, 2.
- состоит из всех возможных наборов длины 3 из трёх элементов: 0, 1, 2.
Это наборы:

Используя функцию  , определим переходы в фазовом пространстве
, определим переходы в фазовом пространстве 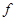 .
.
000 -  ,
,
001 -  ,
,
002 -  ,
,
010 -  ,
,
020 -  ,
,
100 -  ,
,
200 - 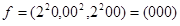 ,
,
111 -  ,
,
110 -  ,
,
112 - 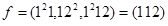 ,
,
101 -  ,
,
121 -  ,
,
011 -  ,
,
211 - 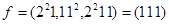 ,
,
222 - 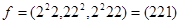 ,
,
220 -  ,
,
221 –  ,
,
202 -  ,
,
212 - 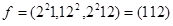 ,
,
022 -  ,
,
122 -  ,
,
012 -  ,
,
021 -  ,
,
210 -  ,
,
102 - 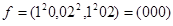 ,
,
120 -  ,
,
210 -  ,
,
201 - 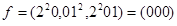 ,
,
Так как  , то
, то 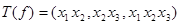 . Используя эту функцию, определим переходы в фазовом пространстве
. Используя эту функцию, определим переходы в фазовом пространстве  .
.
000 - 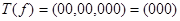 ,
,
001 -  ,
,
010 -  ,
,
100 -  ,
,
101 - 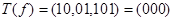 ,
,
011 - 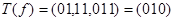 ,
,
110 -  ,
,
111 -  .
.
На рисунке 1.2.1 и 1.2.2 изображены фазовое пространство системы  и ее «Булеанизяция»
и ее «Булеанизяция»  , соответственно.
, соответственно.

Рис. 1.2.1. Фазовое пространство  .
.

Рис. 1.2.2. Фазовое пространство  .
.
Затем связывается  с
с  - размерной линейной системой над конечным кольцом. Заметим сначала что
- размерной линейной системой над конечным кольцом. Заметим сначала что  – изоморфный, как Абелева группа, для
– изоморфный, как Абелева группа, для 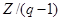 через изоморфизм
через изоморфизм  , появляется возможность генератора для циклической группы
, появляется возможность генератора для циклической группы  . В первую очередь обратим внимание, что множество векторов
. В первую очередь обратим внимание, что множество векторов 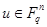 со всеми ненулевыми вхождениями – постоянны для
со всеми ненулевыми вхождениями – постоянны для  .
.
Пусть  – генератор для циклической группы
– генератор для циклической группы  ,и пусть
,и пусть  .
.
Тогда  .
.
Определение 1.2.2.
Обозначим  для
для 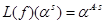 .
.
Видно что  – линейное преобразование
– линейное преобразование  - элемента. Но можно рассматривать его, как линейное преобразование для
- элемента. Но можно рассматривать его, как линейное преобразование для  - элемента, рассматривая
- элемента, рассматривая  как конечное кольцо, которое обозначим –
как конечное кольцо, которое обозначим –  . То есть, имеется линейное преобразование
. То есть, имеется линейное преобразование  .
.
Это доказывает следующую лемму.
Лемма 1.2.2.
 - коммутативная диаграмма.
- коммутативная диаграмма.
Обратим внимание, что вертикальные стрелки – изоморфизмы. Это значит, что они сохраняют фазовое пространство структуры, включая длину конечных циклов. В частности, имеется следующее следствие.
Следствие 1.2.3.
Фазовое пространство  изоморфно к подграфу фазового пространства
изоморфно к подграфу фазового пространства  , состоя из всех наборов с базисным вектором
, состоя из всех наборов с базисным вектором  .
.
Пример 1.2.2.
Для мономиальной системы  в примере 1.2.1,
в примере 1.2.1, 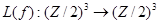 определим
определим  , где
, где
 .
.
Рассчитаем переходы в фазовом пространстве  .
.
000 -  ,
,
001 -  ,
,
010 - 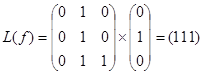 ,
,
011 -  ,
,
100 -  ,
,
101 -  ,
,
110 -  ,
,
111 - 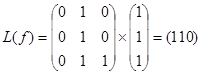 .
.
Фазовое пространство  изображено на рисунке 1.2.3.
изображено на рисунке 1.2.3.

Рис. 1.2.3. Фазовое пространство  .
.
Теорема 1.2.1.
Пусть 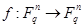 – мономиальная динамическая система. Тогда
– мономиальная динамическая система. Тогда  – система конечных элементов тогда, и только тогда, когда
– система конечных элементов тогда, и только тогда, когда  и
и  – системы конечных элементов.
– системы конечных элементов.
Доказательство.
Из следствий 1.2.1 и 1.2.3, если  – система конечных элементов, то
– система конечных элементов, то  и
и  тоже системы конечных элементов. Для доказательства от противного, предположим что
тоже системы конечных элементов. Для доказательства от противного, предположим что  и
и  – системы конечных элементов, а
– системы конечных элементов, а  – нет. Для каждого конечного цикла
– нет. Для каждого конечного цикла  , любой из двух связанных наборов имеет все координаты ненулевые, или все наборы имеют минимум одну нулевую координату. В первом случае из этого следует, что
, любой из двух связанных наборов имеет все координаты ненулевые, или все наборы имеют минимум одну нулевую координату. В первом случае из этого следует, что  имеет конечный цикл, той же длины. Следовательно, если
имеет конечный цикл, той же длины. Следовательно, если  имеет конечный цикл длины большей чем
имеет конечный цикл длины большей чем  , тогда включаются только наборы имеющие минимум одну нулевую координату.
, тогда включаются только наборы имеющие минимум одну нулевую координату.
Пусть 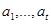 – наборы в конечном цикле. Так как этот конечный цикл должен отображать конечный элемент для
– наборы в конечном цикле. Так как этот конечный цикл должен отображать конечный элемент для  из этого следует, что
из этого следует, что 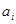 имеет тот же самый базисный вектор, то есть, тот же самый образец нулевых вхождений, и отличается только в ненулевых координатах. Кроме того, мономы в ненулевых координатах не включают никакие переменные, соответствующие нулевым координатам. Таким образом, если построить новый набор
имеет тот же самый базисный вектор, то есть, тот же самый образец нулевых вхождений, и отличается только в ненулевых координатах. Кроме того, мономы в ненулевых координатах не включают никакие переменные, соответствующие нулевым координатам. Таким образом, если построить новый набор 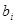 , заменяя каждый
, заменяя каждый  в
в 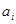 , на
, на  ,
, 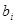 – будет частью конечного цикла длины, по крайней мере
– будет частью конечного цикла длины, по крайней мере  , что является противоречием. Это доказывает теорему.
, что является противоречием. Это доказывает теорему.
|
из
5.00
|
Обсуждение в статье: Сокращение мономиальных систем |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

