Итерационные методы решения нелинейных уравнений

Введение

Целью нашей работы является сравнительный анализ численных методов, таких как итерация, интерполяция, численное дифференцирование и интегрирование, а также метод Эйлера.

В настоящее время появилось значительное число различных программных продуктов (MathCAD, MathLAB и т.д.), с помощью которых, задавая только входные данные, можно решить значительное число задач.

Для более глубокого анализа численных методов очень удобно использовать средства MathCAD, а также алгоритмические языки программирования.

Задание:

По итерационным методам решения нелинейных уравнений:

Определить корень в заданном или выбранном отрезке методом хорд, касательных и простой итерации.

Используя результаты решений, указать наименьший полученный отрезок, в котором содержится корень уравнения.

Для каждого метода и каждой задачи построить график функции на [a, b] и убедиться в выполнении условия сходимости итерационной процедуры.

Используя функции F ( x) из п.1, построить интерполяционный многочлен L₄ ( x) на [a, b], использовав в качестве узловых a и b, остальные необходимые узловые точки выбрать, разделив промежуток [a, b] на почти равные части. Вычислить значения F ( x) и L₄ ( x) в двух точках, одна из которых - середина крайней части, а вторая - середина части, содержащей точку 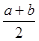. Сравнить полученные величины. Используя эти же узловые точки, провести обратную интерполяцию и определить значение х при y=0. Полученный результат сравнить с ранее найденным решением уравнения.

Сравнить результаты решения СЛАУ методом простой итерации и методом Зейделя на различных шагах итерации.

Провести сравнительный анализ различных методов численного дифференцирования и интегрирования.

Найти численное решение обыкновенного дифференциального уравнения методом Эйлера и уточненным методом Эйлера с 5-ю и 20-ю шагами и сравнить их, если возможно с результатом точного решения ОДУ.

Итерационные методы решения нелинейных уравнений

Задача нахождения корней нелинейных уравнений вида F ( x) =0, где F ( x) - непрерывная функция, - встречается в различных областях научных исследований. Корнам (или решением) уравнения F ( x) =0 называется значение , при котором . Методы решения нелинейных уравнений делятся на:

прямые;

итерационные.

Прямые методы позволяют записать корни в виде некоторого конечного соотношения (формулы). Такие методы применяются для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений.

Однако, на практике встречаются уравнения, которые не удается решить простыми методами. Тогда используются итерационные методы решения, т.е. методы последовательных приближений.

Алгоритм нахождения корня нелинейного уравнения с помощью итерационного метода состоит из двух этапов:

этап локализации (или отделения) корней;

этап итерационного уточнения.

Локализация корней. Отрезок [a, b], содержащий только один корень 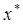уравнения F ( x) =0, называют отрезком локализации корня 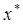. Цель этапа локализации считают достигнутой, если для каждого из подлежащих определению корня удалось указать отрезок локализации (его длину по возможности стараются сделать минимальной). Прежде чем переходить к отыскиванию отрезков локализации, имеет смысл провести предварительное исследование задачи для выяснения того, существует ли вообще корни уравнения и как они расположены на числовой оси. Начальное приближение может быть найдено различными способами: из физических соображений, с помощью графических методов и т.д. Если оценку исходного приближения провести не удается, то находят две близко расположенные точки a и b, в которых непрерывная функция F ( x) принимает значения разных знаков, т.е. F ( a) F ( b) <0. При выполнении этого условия, можно говорить, что между точками a и b есть, по крайней мере, одна точка, в которой F ( x) =0.

Итерационное уточнение корней. На этом этапе для вычисления каждого из корней с точностью 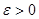 используют тот или иной итерационный метод, позволяющий построить последовательность х₁, х₂, х₃, …_, х _k, … приближений к корню . Итерационный процесс состоит в последовательном уточнении начального приближения х₀. Каждый такой шаг называется итерацией. В результате итераций находится последовательность приближенных значений корня х₁, х₂, х₃, …_, х _k, … Если эти значения с ростом k стремятся к истинному значению корня , то говорят, итерационный процесс сходится.

Метод хорд

Пусть мы нашли отрезок [a, b], на котором функция F ( x) меняет знак. Для определенности примем F ( a) >0, F ( b) <0. В данном методе процесс итераций состоит в том, что в качестве приближений корню уравнения принимаются значения х₀, х₁,… точек пересечения хорды с осью абсцисс.

Сначала найдем уравнение хорды АВ:

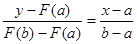
Для точки пересечения ее с осью абсцисс (y=0) получим уравнение

.

Далее, сравнивая знаки величин F ( a) и F ( x) для рассматриваемого случая, приходим к выводу, что корень находится в интервале (a, x), так как F ( a) *F ( x) <0 (условие существование корня). Отрезок [x, b] отбрасываем и больше не рассматриваем. Следующая итерация состоит в определении нового приближения x_n как точки пересечения хорды АВ₁ с осью абсцисс и так далее. На рисунке 1 изображена геометрическая интерпретация нахождение решения методом хорд.

Рисунок 1 - Метод хорд

При решении уравнения методом хорд поводится прямая соединяющая концы отрезка [a,b]. Из двух точек А и В выбирается х₀. Находится точка пересечения хорды с осью OX. Определяется значение функции в точке пересечения и из найденной точки проводится новая хорда. Этот процесс повторяется до получения необходимой точности.

Формула для n-го приближения имеет вид (х₀=а, x_n-1= b, x_n= x):

В методе хорд условием окончания итераций является:

условие близости двух последовательных приближений: ;

условие малости невязки  (величина F ( x_n) есть невязка, полученная на n-й итерации, а -число, с заданной точностью которого необходимо найти решение).