 |
Главная |
Практическое применение метода хорд
|
из
5.00
|
Исследование функции
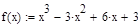
Возьмем для исследования функцию 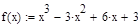 и определим точность решения как
и определим точность решения как  =0,001.
=0,001.
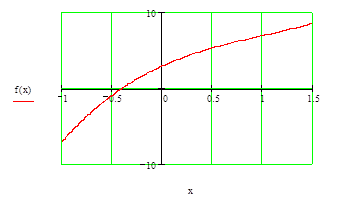
Рисунок 2 - График функции 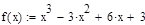
Визуально определяем границы отрезка, на котором находится корень. Выделяем отрезок [a,b], (а= -0,45, b= -0,3).
1. Проверяем существование корня на отрезке по условию 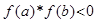 :
:
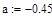
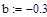
Убедимся, что функция принимает на концах указанных отрезков значения разных знаков
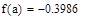


0,36<0
Условие выполнено, следовательно, на данном промежутке корень есть.
2. Далее исследуем функцию на монотонность:
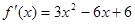

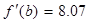
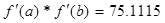
75.1115>0
Экстремумов на выбранном отрезке нет.
3. Проверяем функцию на единственность корня
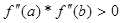
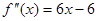
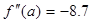
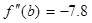
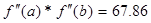
67.86>0
На данном промежутке имеется только один корень
4. Выбор точки х0 зависит от того совпадает ли её знак со знаком второй производной данной функции.
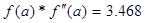
 >0
>0
Из условия следует, что х0= a=-0.45, тогда за х1 принимаем b - х1= b=-0.3
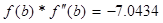
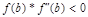
5. Исходя из графика мы приняли за x0=-0.45 и x1=-0.3. Найдем значение функции в этих точках:
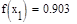
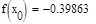
Формула для решения
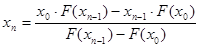
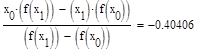
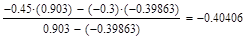
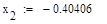
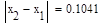
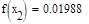
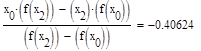
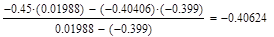
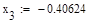

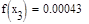

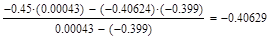
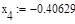
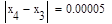


Условие выполнено, необходимая точность достигнута. Итерационный процесс можно прекратить. Добиться указанной точности нам удалось на 4-ой проведенной итерации.
Исследование функции
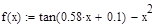
Возьмем для исследования функцию 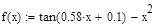 и определим точность решения как
и определим точность решения как  =0,001.
=0,001.
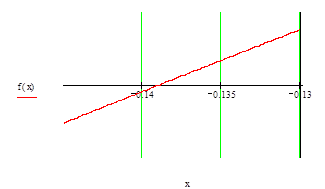
Рисунок 3 - График функции 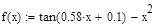
Визуально определяем границы отрезка, на котором находится корень. Выделяем отрезок [a,b], (а=-0,4, b=0,1).
1. Проверяем существование корня на отрезке по условию 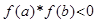 :
:
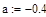
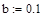
Убедимся, что функция принимает на концах указанных отрезков значения разных знаков

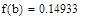
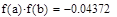
0,04327 <0
Условие выполнено, следовательно, на данном промежутке корень есть.
2. Далее исследуем функцию на монотонность:

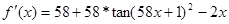
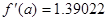
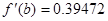
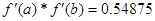
Экстремумов на выбранном отрезке нет.
3. Проверяем функцию на единственность корня:

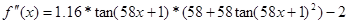
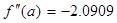
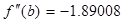
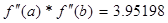
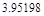 >0
>0
На данном промежутке имеется только один корень.
4) Выбор точки х0 зависит от того совпадает ли её знак со знаком второй производной данной функции.
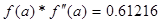
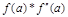 >0
>0
Из условия следует, что х0= a=-0.4, тогда за х1 принимаем b - х1= b=0.1
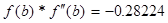
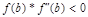
5. Исходя из графика мы приняли за x0=-0.4 и x1=0.1. Найдем значение функции в этих точках:
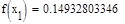
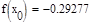
Формула для решения
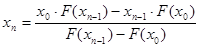

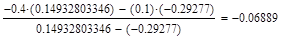
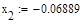
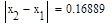
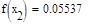
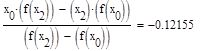
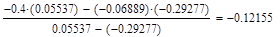
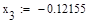
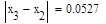
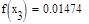
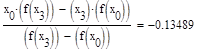
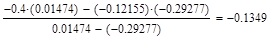
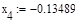
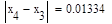

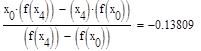
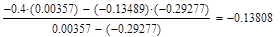
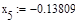
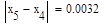
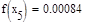
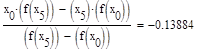
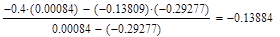
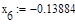
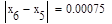
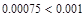

Условие выполнено, необходимая точность достигнута. Итерационный процесс можно прекратить. Добиться указанной точности нам удалось на 6-ой проведенной итерации.
Метод касательных
Его отличие от предыдущего метода состоит в том, что на k-й итерации вместо хорды проводится касательная к кривой y= F ( x) при х= ck-1 и ищется точка пересечения касательной с точкой абсцисс. При этом необязательно задавать отрезок [a, b], содержащий корень уравнения, а достаточно лишь найти некоторое начальное приближение корнях.
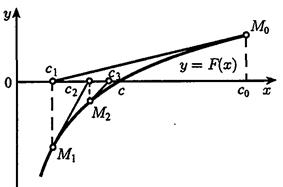
Рисунок 4 - Метод касательных
Уравнение касательной, проведенной к кривой y= F ( x) в некоторой точке с координатами х0 и F (х0) имеет вид:
y- F (х0) = F’ (х0) ( x-х0).
Отсюда найдем следующее приближение корня х как абсциссу точки пересечения касательной с осью х (у=0):
х=х0 - F (х0) / F’ (х0).
Аналогично могут быть найдены и следующие приближения как точки пересечения с осью абсцисс касательных. Формула для n-го приближения имеет вид:
х n=х n-1 - F (х n-1) / F’ (х n-1), n=1,2,…
При этом необходимо, чтобы выполнялось условие F’ (х n-1) 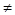 0.
0.
Для окончания итерационного процесса используются те же условия, что и в методе хорд.
|
из
5.00
|
Обсуждение в статье: Практическое применение метода хорд |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

