Мегаобучалка Главная | О нас | Обратная связь


Модификация метода Эйлера:



2019-12-29 221 Обсуждений (0)
Модификация метода Эйлера: 0.00 из 5.00 0 оценок




Усовершенствованный метод Эйлера

 

Рассмотрим уравнение  в окрестностях узлов . В левой части уравнения  заменим производную центральной разностью

 

,

 

а правую часть оставим без изменений:

 

.


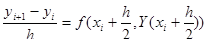Приближенное значение функции 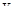 в точке  вычислим с помощью метода Эйлера:

 

.

 

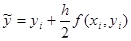Выразим  из

 

,

 

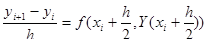заменив  его приближением :

 

 

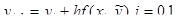
Данный метод имеет второй порядок точности.

 

Практическое применение метода Эйлера

 

Исходное ОДУ:

 

y (1,8) =2,6,

 

Таблица 1. метод Эйлера (n=5)

i

xi

yi+1

f (xi,yi)

h*f (xi,yi)

0

1,8

3.0393624

2.1968119

0.4393624

1

2

3.4813579

2.2099777

0.4419955

2

2,2

3.9241350

2.2138853

0.4427771

3

2,4

4.3675167

2.2169085

0.4433817

4

2,6

4.8128840

2.2268365

0.4453673

5

2,8

5.2630132

2.2506461

0.4501292

 

Таблица 2. метод Эйлера (n=20)

i

xi

yi+1

f (xi,yi)

h*f (xi,yi)

0

1,8

2.7098405952

2.1968119048

0.1098405952

1

1,85

2.8199037007

2.2012621087

0.1100631054

2

1,9

2.9301422065

2.2047701167

0.1102385058

3

1,95

3.0405154109

2.2074640873

0.1103732044

4

2

3.1509890866

2.2094735145

0.1104736757

5

2,05

3.2615355030

2.2109283275

0.1105464164

6

2,1

3.3721334073

2.2119580866

0.1105979043

7

2,15

3.4827679715

2.2126912836

0.1106345642

8

2,2

3.5934307091

2.2132547518

0.1106627376

9

2,25

3.7041193685

2.2137731878

0.1106886594

10

2,3

3.8148378077

2.2143687841

0.1107184392

11

2,35

3.9255958562

2.2151609716

0.1107580486

12

2,4

4.0364091696

2.2162662661

0.1108133133

13

2,45

4.1472990802

2.2177982138

0.1108899107

14

2,5

4.2582924517

2.2198674293

0.1109933715

15

2,55

4.3694215376

2.2225817186

0.1111290859

16

2,6

4.4807238516

2.2260462796

0.1113023140

17

2,65

4.5922420502

2.2303639716

0.1115181986

18

2,7

4.7040238326

2.2356356483

0.1117817824

19

2,75

4.8161218599

2.2419605453

0.1120980273

20

2,8

4.9285936957

2.2494367159

0.1124718358

 

Практическое применение уточненного метода Эйлера

 

 

Таблица 3. метод Эйлера (n=5)

i

xi

yi

f (xi,yi)

h*f (xi,yi)

0

1,8

3.0408296

2.1968119

0.1098406

1

2

3.5034503

2.2093361

0.1104668

2

2,2

3.9875064

2.2040057

0.1102003

3

2,4

4.4928015

2.1891243

0.1094562

4

2,6

5.0193000

2.1754674

0.1087734

5

2,8

5.5671264

2.1759596

0.1087980

 

Таблица 4. метод Эйлера (n=20)

i

xi

yi

f (xi,yi)

h*f (xi,yi)

0

1,8

2.7099548

2.1968119

0.1098406

1

1,85

2.8213531

2.2012143

0.1100607

2

1,9

2.9341858

2.2041527

0.1102076

3

1,95

3.0484445

2.2057163

0.1102858

4

2

3.1641214

2.2060049

0.1103002

5

2,05

3.2812091

2.2051292

0.1102565

6

2,1

3.3997009

2.2032109

0.1101605

7

2,15

3.5195904

2.2003825

0.1100191

8

2,2

3.6408721

2.1967877

0.1098394

9

2,25

3.7635409

2.1925804

0.1096290

10

2,3

3.8875922

2.1879256

0.1093963

11

2,35

4.0130221

2.1829984

0.1091499

12

2,4

4.1398272

2.1779839

0.1088992

13

2,45

4.2680046

2.1730767

0.1086538

14

2,5

4.3975522

2.1684808

0.1084240

15

2,55

4.5284683

2.1644085

0.1082204

16

2,6

4.6607518

2.1610801

0.1080540

17

2,65

4.7944021

2.1587230

0.1079362

18

2,7

4.9294193

2.1575712

0.1078786

19

2,75

5.0658041

2.1578639

0.1078932

20

2,8

5.2035577

2.1598449

0.1079922

 

Поправка Ричардсона Ri для метода Эйлера:

 

 

-0.07065289342943
-0.13216188575150
-0.18444601911606
-0.26010250688842
-0.33631248297229
-0.41398824090458

 

Поправка Ричардсона Ri для метода Рунге-Кутта:

 

 

-0.07315885784
-0.15166859920
-0.23543241393
-0.32440371076
-0.41858637980
-0.51803478491

 

Заключение

 

В ходе выполнения курсовой работы был проведен сравнительный анализ численных методов, таких как итерация, интерполяция, численное дифференцирование и интегрирование, а также метод Эйлера.

В настоящее время появилось значительное число различных программных продуктов (MathCAD, MathLAB и т.д.), с помощью которых, задавая только входные данные, можно решить значительное число задач.

Для более глубокого анализа численных методов мы использовали средства MathCAD, а также алгоритмические языки программирования.

Список используемой литературы

 

1. Р.Ф. Хемминг "Численные методы (для научных работников и инженеров)". - Москва, 1972.

2. А.А. Амосов, А.Ю. Дубинский, Н.В. Копченова "Вычислительные методы для инженеров". - Москва, "Высшая школа", 1994.

3. Ф.В. Формалев, Д.Л. Ревизников "Численные методы". - М.: ФИЗМАТЛИТ, 2004.

4. Ю. Тарасевич "Численные методы на MathCAD’e". - Астраханский гос. пед. ун-т: Астрахань 2000.



2019-12-29 221 Обсуждений (0)
Модификация метода Эйлера: 0.00 из 5.00 0 оценок








Обсуждение в статье: Модификация метода Эйлера:

Обсуждений еще не было, будьте первым... ↓↓↓

Отправить сообщение

Популярное:
Почему двоичная система счисления так распространена?: Каждая цифра должна быть как-то представлена на физическом носителе...
Почему люди поддаются рекламе?: Только не надо искать ответы в качестве или количестве рекламы...
Модели организации как закрытой, открытой, частично открытой системы: Закрытая система имеет жесткие фиксированные границы, ее действия относительно независимы...
Почему человек чувствует себя несчастным?: Для начала определим, что такое несчастье. Несчастьем мы будем считать психологическое состояние...



©2015-2024 megaobuchalka.ru Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. (221)

Почему 1285321 студент выбрали МегаОбучалку...

Система поиска информации

Мобильная версия сайта

Удобная навигация

Нет шокирующей рекламы

(0.007 сек.)