Построение гистограммы

 

Разделяем вариационный ряд на интервалы. Статистическая вероятность попадания i-ого результата в данный интервал находим по формуле:

 

где n- частота попадания результатов в каждый k-й интервал.

 

 

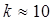
Вычисляем ширину интервала по формуле :

 

 

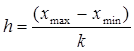
Определяем границы интервалов, затем определяем частоту попадания в интервалы и середины интервалов. Результаты расчетов сводим в таблицу 3.

 

Таблица 3 - Промежуточные значения интервального ряда

Границы интервалов xi - xi+1	Середина интервалов xi0	Частота попадания mi	Статистическая вероятность pi
1	2	3	4
0,5 – 0,55	0,525	19	0,19
0,55 – 0,60	0,575	5	0,05
0,60 – 0,65	0,625	7	0,07
0,65 – 0,70	0,675	40	0,40
0,70 – 0,75	0,725	9	0,09
0,75 – 0,80	0,775	1	0,01
0,80 – 0,85	0,825	3	0,03
0,85 – 0,90	0,875	1	0,01
0,90 – 0,95	0,925	0	0,00
0,95 – 1,00	0,975	15	0,15

 

Представим заданный статистический ряд в виде гистограммы (Приложение А, рисунок А.1).

 

2.5 Определение коэффициента точности:

 

, где

 

6 S- поле рассеивания;

U-l- ширина поля допуска

 

 

Вывод: процесс обеспечивает более высокую точность, чем требует НТД.

 

2.6 Определение коэффициента настроенности:

 

, где

 

- значение смещения вершины кривой распределения случайной величины от середины поля допуска.

 

, где

 

- середина поля допуска

- середина интервала

 

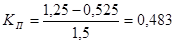- для 1-го интервала;

- для 2-го интервала;

 - для 3-го интервала;

- для 4-го интервала;

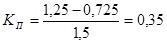- для 5-го интервала;

 - для 6-го интервала;

- для 7-го интервала;

- для 8-го интервала;

 - для 9-го интервала;

 - для 10-го интервала.

 

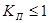
Вывод: т.к коэффициент настроенности меньше 1 с вероятностью 0,997 можно сказать, что процесс настроен.

 

2.7 Определяем фактический коэффициент настройки:

 

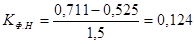 для 1-го интервала;

 для 2-го интервала;

 для 3-го интервала;

 для 4-го интервала;

 для 5-го интервала;

 для 6-го интервала;

 для 7-го интервала;

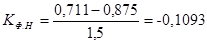 для 8-го интервала;

 для 9-го интервала;

 для 10-го интервала;

 

Вывод: т.к коэффициент настроенности меньше 1 с вероятностью 0,997 можно сказать, что процесс настроен.

 

2.8 Определение допустимого коэффициента точности:

 

Вывод: с вероятностью 0,997 можно сказать, что процесс точен.

 

2.9 Определение коэффициента запаса точности ( является резервом на смещение наладки технологического процесса):

 

 

Вывод: с вероятностью 0,997 можно сказать, что резерв на смещение технологического процесса равен 97%.

 

2.10 Определение коэффициента стабильности:

 

, где

 

- оценка СКО в фиксированный момент времени.

- оценка СКО в сравнительный момент времени.

Разобьем выборку n=100 на группы по 20 значений и для каждой определим  и СКО.

Для первой группы:

Для второй группы:

Для третьей группы:

Для четвертой группы:

Для пятой группы:

Тогда:

 

; ; ;

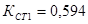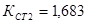Т.к коэффициенты стабильности отличаются друг от друга, следовательно, технологический процесс нестабилен.

ВЫВОД: с вероятностью 0,997 можно сказать, что технологический процесс точен, но не стабилен.