 |
Главная |
Основные теоремы о сравнениях
|
из
5.00
|
Введение
Методы теории сравнений широко применяются в различных областях науки, техники, экономики. Этот раздел алгебры занимает важное место в вузовском образовании математиков, физиков и других специалистов, однако очень часто изучается недостаточно глубоко. Задача данной курсовой работы – изучить теоретический материал и рассмотреть ряд основополагающих задач по одному из основных разделов теории чисел: сравнения первой степени с одной и несколькими переменными, сравнения высших степеней и т.д.
Основная часть курсовой работы состоит из трех глав. В первой главе раскрываются основные понятия теории сравнений, такие как сравнения в кольце целых чисел, основные теоремы и свойства сравнений. Во второй главе рассматриваются сравнения первой степени с одной переменной. Далее рассматриваются сравнения высших степеней и системы сравнений первой степени. В приложении приводятся примеры решения текстовых задач, которые сводятся к неопределенным уравнениям первого порядка и решаются с помощью сравнений.
Изложение теоретического материала иллюстрируется большим количеством примеров с подробными решениями.
В работе приводится список литературы по теме.
Теория сравнений
Сравнения в кольце целых чисел
Понятие сравнения было введено впервые Гауссом. Несмотря на свою кажущуюся простоту, это понятие очень важно и имеет много приложений.
Возьмем произвольное фиксированное натуральное число  и будем рассматривать остатки при делении на m различных целых чисел. При рассмотрении свойств этих остатков и произведении операций над ними удобно ввести понятие так называемого сравнения по модулю.
и будем рассматривать остатки при делении на m различных целых чисел. При рассмотрении свойств этих остатков и произведении операций над ними удобно ввести понятие так называемого сравнения по модулю.
Определение. Целые числа 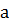 и
и  называются сравнимыми по модулю
называются сравнимыми по модулю  , если разность
, если разность  делится на
делится на  , т.е. если
, т.е. если  .
.
Таким образом, сравнение представляет собой соотношение между тремя числами  и
и  , причем
, причем  , играющее роль своего рода эталона сравнения, мы называем «модулем». Для краткости будем это соотношение между
, играющее роль своего рода эталона сравнения, мы называем «модулем». Для краткости будем это соотношение между  и
и  записывать:
записывать:
 , ,
|
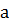 и
и  будем называть соответственно левой и правой частями сравнения. Число
будем называть соответственно левой и правой частями сравнения. Число  , стоящее под знаком модуля, будем всегда считать положительным, т.е. запись
, стоящее под знаком модуля, будем всегда считать положительным, т.е. запись  будет означать, что
будет означать, что  .
.
Если разность  не делится на
не делится на  , то мы будем записывать:
, то мы будем записывать:
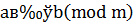 .
.
Согласно определению, 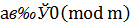 означает, что
означает, что 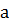 делится на
делится на  .
.
Примеры.
1.  так как
так как  и
и 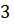 делится на
делится на  .
.
2.  , так как
, так как 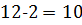 и
и  делится на
делится на  .
.
3.  , так как
, так как  и
и  делится на
делится на  .
.
Основные теоремы о сравнениях
Теорема 1 (признак сравнимости двух чисел по модулю  ). Два целых числа
). Два целых числа 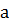 и
и  сравнимы по модулю
сравнимы по модулю  тогда и только тогда, когда
тогда и только тогда, когда 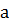 и
и  имеют одинаковые остатки при делении на
имеют одинаковые остатки при делении на  .
.
Доказательство. Пусть остатки при делении 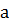 и
и  на
на  равны, т.е.
равны, т.е.

| (1.1) |

| (1.2) |
где 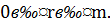
Вычтем (1.2) из (1.1); получим  т.е.
т.е.  или
или 
Обратно, пусть  это означает, что
это означает, что  или
или

| (1.3) |
Разделим  на
на  ; получим
; получим  Подставив
Подставив  в (1.3), будем иметь
в (1.3), будем иметь  т.е. при делении
т.е. при делении 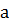 на
на  получается тот же остаток, что и при делении
получается тот же остаток, что и при делении  на
на  .
.
Пример 1. Определим, сравнимы ли числа  и
и  по модулю
по модулю  .
.
Решение. При делении  и
и  на
на  получаются одинаковые остатки
получаются одинаковые остатки  Следовательно,
Следовательно, 
Определение. Два или несколько чисел, дающие при делении на  одинаковые остатки, называются равноостаточными или сравнимыми по модулю
одинаковые остатки, называются равноостаточными или сравнимыми по модулю  .
.
Теорема 2. Отношение сравнимости рефлексивно:  .
.
Доказательство.  и
и  имеют одинаковые остатки при делении на
имеют одинаковые остатки при делении на  .
.
Теорема 3. Отношение сравнимости симметрично: если  , то
, то  .
.
Доказательство. Если 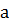 и
и  имеют одинаковые остатки при делении на
имеют одинаковые остатки при делении на  , то остатки от деления
, то остатки от деления  и
и 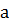 на
на  также равны.
также равны.
Теорема 4. Отношение сравнимости транзитивно: если 
 то
то  .
.
Доказательство. Если остатки от деления на  одинаковы у чисел
одинаковы у чисел 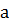 и
и  , а также у
, а также у  и
и 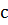 , то
, то 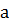 и
и 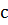 тоже имеют одинаковые остатки при делении на
тоже имеют одинаковые остатки при делении на  .
.
Таким образом, отношение сравнимости есть отношение эквивалентности.
Теорема 5. Если  и
и  произвольное целое число, то
произвольное целое число, то
 .
.
Доказательство. Если  , то
, то  ,
,  ,
,  ,
,  .
.
Теорема 6. Если  и
и 
 1, то
1, то  .
.
Доказательство. Если  , то
, то  |
| 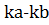 ,
,  |
|  , но тогда условие
, но тогда условие  дает
дает  |
|  , т.е.
, т.е.  .
.
Теорема 7. Если  и
и  произвольное натуральное число, то
произвольное натуральное число, то  .
.
Доказательство. Если  , то
, то  |
|  ,
,  |
| 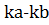 ,
,  .
.
Теорема 8. Если  , где
, где 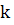 и
и 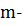 произвольные натуральные числа, то
произвольные натуральные числа, то  .
.
Доказательство. Если  , то
, то 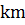 |
| 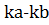 ,
, 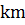 |
|  ,
,
 натуральное (
натуральное (  , тогда
, тогда  |
|  ,
,  .
.
Теорема 9. Если  ,
, 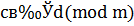 , то
, то  и
и  .
.
Доказательство. Если  и
и 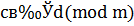 , то
, то  и
и  . Получим, что
. Получим, что 
Теорема 9'. Если  , то
, то  .
.
Теорема 10. Если  и
и 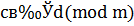 , то
, то 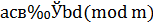 .
.
Доказательство. Если  и
и 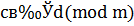 , то
, то  и
и  . Тогда по транзитивности сравнений получим, что
. Тогда по транзитивности сравнений получим, что 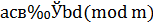 .
.
Теорема 10'. Если  , то
, то
 .
.
Доказательство. Последовательно применяя теорему 7, получим:
 .
.
Теорема 11. Если  , то при любом целом
, то при любом целом  ,
, 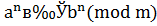 .
.
Доказательство. При  утверждение верно по теореме 2, а при
утверждение верно по теореме 2, а при  оно верно согласно теореме 10', если
оно верно согласно теореме 10', если 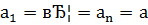 и
и 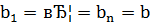 .
.
Переход от сравнений  ,
, 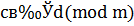 к сравнениям
к сравнениям
 ,
, 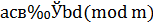 ,
, 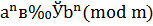
будем называть соответственно сложением (вычитанием), умножением, возведением в степень сравнений.
Так как из сравнения 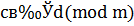 следует
следует  , то из сравнений
, то из сравнений  и
и  следует также, что
следует также, что  и
и  .
.
Теорема 12. Если  и
и  произвольный многочлен с целыми коэффициентами, то
произвольный многочлен с целыми коэффициентами, то  .
.
Доказательство. Если  , то, согласно теоремам 7 и 11, имеем:
, то, согласно теоремам 7 и 11, имеем:
 при
при  .
.
По теореме 9', получаем  ,
,
т.е.  .
.
Теорема 12'. Если  и
и  многочлен с целыми коэффициентами, то
многочлен с целыми коэффициентами, то
 .
.
Теорема 13. Любое слагаемое левой или правой части сравнения можно перенести с противоположным знаком в другую часть.
Доказательство. Ввиду симметричности отношения сравнения достаточно рассмотреть случай, когда дано сравнение 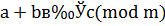 . Складывая это сравнение со сравнением
. Складывая это сравнение со сравнением  , получаем
, получаем  .
.
Следствие. В левой и правой частях сравнения можно добавлять или отбрасывать одно и то же слагаемое.
Теорема 14. В сравнении можно отбрасывать или добавлять слагаемые, делящиеся на модуль.
Доказательство. Если  и
и  , т.е.
, т.е.  , то, складывая эти сравнения, получаем
, то, складывая эти сравнения, получаем  . Аналогично из
. Аналогично из  и
и  получаем
получаем  .
.
Поскольку левую и правую части сравнения можно менять местами, утверждение верно и для слагаемых правой части.
Теорема 15. Если  и
и  , то
, то  .
.
Доказательство. Если  , то
, то  . Из
. Из  ,
,  в силу транзитивности отношения делимости получаем
в силу транзитивности отношения делимости получаем  ,
,  .
.
Теорема 16. Если  , то множество общих делителей
, то множество общих делителей 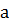 и
и  совпадает с множеством общих делителей
совпадает с множеством общих делителей  и
и  . В частности,
. В частности, 
Доказательство. Если  , то
, то  ,
,  ,
,  , любой общий делитель
, любой общий делитель  чисел
чисел 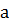 и
и  является общим делителем чисел
является общим делителем чисел  и
и  , и, наоборот, если
, и, наоборот, если  и
и  , то
, то  .
.
Поскольку пара  и пара
и пара  имеют одни и те же общие делители, то и
имеют одни и те же общие делители, то и  .
.
Теорема 17. Если  ,
,  , то
, то  , где
, где  .
.
Доказательство. Если  ,
,  , то
, то  , то
, то  и, согласно свойствам наименьшего общего кратного,
и, согласно свойствам наименьшего общего кратного,  .
.
|
из
5.00
|
Обсуждение в статье: Основные теоремы о сравнениях |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

