 |
Главная |
Теоремы об эквивалентных сравнениях
|
из
5.00
|
Теорема 1.Пусть дано сравнение
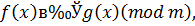
| (3.6) |
где 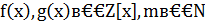 .
.
Тогда имеют место следующие утверждения:
1) Если к обеим частям сравнения (3.6) прибавить любой многочлен  то получится сравнение, эквивалентное сравнению (3.6).
то получится сравнение, эквивалентное сравнению (3.6).
2) Если обе части сравнения (3.6) умножить на одно и то же целое число, взаимно простое с модулем, то получится сравнение, эквивалентное сравнению (3.6).
3) Если обе части сравнения и модуль умножить на одно и то же натуральное число  , то получится сравнение, эквивалентное сравнению (3.6).
, то получится сравнение, эквивалентное сравнению (3.6).
Доказательство.
1) Пусть класс вычетов  но модулю
но модулю 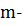 решение сравнения (3.6), то есть для
решение сравнения (3.6), то есть для  сравнение
сравнение
2)
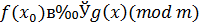
| (3.7) |
является верным сравнением, следовательно, сравнение
 , ,
| (3.8) |
где  , тоже верно. Поэтому класс вычетов
, тоже верно. Поэтому класс вычетов  по модулю
по модулю  является решением сравнения
является решением сравнения

| (3.9) |
Обратное также верно: если 
 решение сравнения (3.9), то для
решение сравнения (3.9), то для  , будет верно сравнение (3.8), а, следовательно, верно сравнение (3.7), поэтому
, будет верно сравнение (3.8), а, следовательно, верно сравнение (3.7), поэтому  является решением сравнения (3.6).
является решением сравнения (3.6).
Таким образом, сравнения (3.6) и (3.9) эквивалентны.
3) Пусть класс вычетов  по
по  – решение сравнения (3.6), тогда для
– решение сравнения (3.6), тогда для  , получим верное сравнение
, получим верное сравнение  . Возьмем целое число
. Возьмем целое число  , взаимно простое с модулем:
, взаимно простое с модулем: 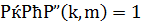 . Умножим последнее сравнение почленно на
. Умножим последнее сравнение почленно на  , получим верное сравнение:
, получим верное сравнение:

| (3.10) |
отсюда получим, что класс вычетов  по модулю
по модулю 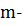 решение сравнения
решение сравнения

| (3.11) |
Обратно, если класс вычетов  по модулю
по модулю  решение сравнения (3.11), то для
решение сравнения (3.11), то для  верно сравнение (3.10), следовательно, будет верно и сравнение:
верно сравнение (3.10), следовательно, будет верно и сравнение:

(заметим, что  , так как
, так как 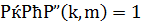 , в противном случае было бы:
, в противном случае было бы:  ). Поэтому класс вычетов
). Поэтому класс вычетов  по модулю
по модулю 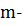 решение сравнения (3.6).
решение сравнения (3.6).
Таким образом, сравнения (3.6) и (3.11), где 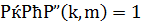 , будут эквивалентными.
, будут эквивалентными.
3) Пусть класс вычетов  по модулю
по модулю 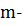 решение сравнения (3.6), тогда для
решение сравнения (3.6), тогда для  верно сравнение
верно сравнение  , а, значит, верно и сравнение
, а, значит, верно и сравнение
4)

| (3.12) |
для любого натурального числа  , поэтому класс вычетов
, поэтому класс вычетов  по модулю
по модулю 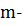 решение сравнения
решение сравнения
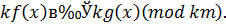
| (3.13) |
Обратно, если класс вычетов  по модулю
по модулю 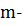 решение сравнения (3.13), то для
решение сравнения (3.13), то для  верно сравнение (3.12), но тогда по свойству сравнений верно сравнение:
верно сравнение (3.12), но тогда по свойству сравнений верно сравнение:  , поэтому класс вычетов
, поэтому класс вычетов  по модулю
по модулю  решение сравнения (3.6). Следовательно, сравнения (3.6) и (3.13) эквивалентны. Теорема доказана.
решение сравнения (3.6). Следовательно, сравнения (3.6) и (3.13) эквивалентны. Теорема доказана.
В дальнейшем сравнение (3.6) можно заменить эквивалентным сравнением:

| (3.14) |
где  Теорема 1 доказана.
Теорема 1 доказана.
Теорема 2. Пусть даны сравнения  Тогда сравнения эквивалентны.
Тогда сравнения эквивалентны.
Доказательство. Умножим почленно верные сравнения на  некоторое целое число:
некоторое целое число:

|
| … |

|

|
Сложим почленно полученные сравнения, тогда получим сравнение:

отсюда получим, что  . Но тогда
. Но тогда  и
и  . Следовательно, сравнения
. Следовательно, сравнения  и
и  эквивалентны. Теорема 2 доказана.
эквивалентны. Теорема 2 доказана.
Заметим, из доказанной теоремы, в частности, следует, что сравнение заменится эквивалентным, если отбросить (или добавить) слагаемое с коэффициентами, делящимися на модуль.
|
из
5.00
|
Обсуждение в статье: Теоремы об эквивалентных сравнениях |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

