 |
Главная |
Сравнения по простому модулю с одним неизвестным
|
из
5.00
|
Переходя от сравнений 1-й степени к сравнениям более высоких степеней, целесообразно сначала рассмотреть тот случай, когда модуль – простое число. В этом случае имеется ряд весьма важных теорем, которые, вообще говоря, неверны для составных модулей. Вместе с тем теория сравнений по простому модулю является основой, на которой строится изучение сравнений по составному модулю.
Во всей этой главе буквой  будем обозначать модуль, представляющий собой простое число.
будем обозначать модуль, представляющий собой простое число.
Теорема 1.Если 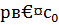 , то сравнение
, то сравнение

может быть заменено эквивалентным сравнением с коэффициентом при старшем члене, равном единице.
Доказательство. Рассмотрим сравнение 1-й степени 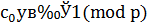 ; поскольку
; поскольку 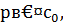 то и сравнение имеет решение. Найдем число
то и сравнение имеет решение. Найдем число  , удовлетворяющее этому сравнению, т.е.
, удовлетворяющее этому сравнению, т.е.  такое, что
такое, что  .
.
Тогда сравнение 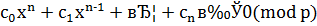 эквивалентно сравнению
эквивалентно сравнению
 ,
,
а следовательно, сравнению
 ,
,
где  .
.
Пример 1. Заменить сравнение

эквивалентным сравнением с коэффициентом при старшем члене, равным 1.
Решаем сравнение  и находим
и находим 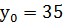 . Данное нам сравнение эквивалентно сравнению
. Данное нам сравнение эквивалентно сравнению
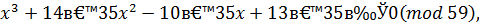
т.е. сравнению  .
.
Теорема 2. Если  и
и  многочлены с целыми коэффициентами, то сравнения по простому модулю
многочлены с целыми коэффициентами, то сравнения по простому модулю

| (3.15) |

| (3.16) |
эквивалентны.
Доказательство. Пусть  удовлетворяет сравнению (3,15), т.е.
удовлетворяет сравнению (3,15), т.е.  . Поскольку при любом
. Поскольку при любом  согласно теореме Ферма
согласно теореме Ферма  , то
, то
 .
.
Пользуясь той же теоремой Ферма, получаем, что если  удовлетворяет сравнению (3,16), то
удовлетворяет сравнению (3,16), то 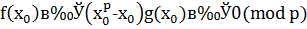 , и, таким образом, сравнения (3,15) и (3,16) эквивалентны.
, и, таким образом, сравнения (3,15) и (3,16) эквивалентны.
Из этой теоремы непосредственно вытекает следующая.
Теорема 3. Сравнение по простому модулю  , степень которого больше, чем этот модуль или равна ему, может быть заменено эквивалентным сравнением степени, меньшей
, степень которого больше, чем этот модуль или равна ему, может быть заменено эквивалентным сравнением степени, меньшей  .
.
Доказательство. Пусть  многочлен с целыми коэффициентами степени
многочлен с целыми коэффициентами степени  . При делении
. При делении  на
на 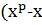 ), частное
), частное 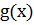 и остаток
и остаток 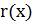 будут также многочленами с целыми коэффициентами:
будут также многочленами с целыми коэффициентами:
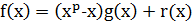 ,
,
где степень 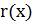 меньше степени
меньше степени 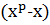 , т.е. меньше, чем
, т.е. меньше, чем  . Согласно предыдущей теореме, сравнения
. Согласно предыдущей теореме, сравнения 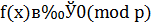 и
и 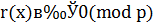 эквивалентны.
эквивалентны.
Пример 2. Сравнение 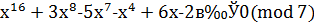 заменить эквивалентным сравнением степени, меньшей чем 7.
заменить эквивалентным сравнением степени, меньшей чем 7.
Решение. Мы получим эквивалентное сравнение, если заменим  на
на  ,
,  на
на  ,
,  на
на 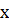 . Таким образом, заданное сравнение эквивалентно сравнению
. Таким образом, заданное сравнение эквивалентно сравнению

т.е. сравнению  .
.
Теорема 4.Если  многочлены с целыми коэффициентами:
многочлены с целыми коэффициентами: 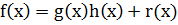 , и все коэффициенты
, и все коэффициенты 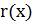 делятся на простое число
делятся на простое число  , то любое решение сравнения
, то любое решение сравнения

| (3.17) |
является решением, по крайней мере, одного из сравнений:
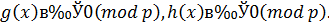
| (3.18) |
Доказательство. Пусть  решение сравнения (3.17), т.е.
решение сравнения (3.17), т.е.  . Поскольку все коэффициенты
. Поскольку все коэффициенты 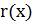 делятся на
делятся на  , будем также иметь
, будем также иметь 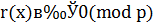 , поэтому
, поэтому

Из сравнимости произведения 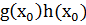 с нулем по модулю
с нулем по модулю  следует, что по крайней мере один из этих множителей сравним с нулем по этому модулю, т.е.
следует, что по крайней мере один из этих множителей сравним с нулем по этому модулю, т.е.  решение по крайней мере одного из сравнений (3.18).
решение по крайней мере одного из сравнений (3.18).
Пример 3. В сравнении  левую часть можно представить в виде
левую часть можно представить в виде 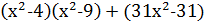 , и мы находим все решения этого сравнения, решая сравнения:
, и мы находим все решения этого сравнения, решая сравнения: 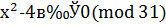 ,
,  , т.е.
, т.е. 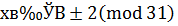 и
и 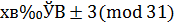 . Все эти четыре класса удовлетворяют нашему сравнению.
. Все эти четыре класса удовлетворяют нашему сравнению.
Для составных модулей эта теорема неверна. Например, сравнению
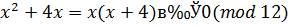
удовлетворяет класс 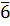 , не являющийся решением ни одного из сравнений:
, не являющийся решением ни одного из сравнений:
 ,
, 
Теорема 5.Сравнение степени  по простому модулю
по простому модулю  с коэффициентом при старшем члене, не делящимся на
с коэффициентом при старшем члене, не делящимся на  , может иметь не больше чем
, может иметь не больше чем  решений.
решений.
Доказательство. Утверждение теоремы верно при 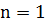 . Действительно, в этом случае мы имеем сравнение 1-й степени:
. Действительно, в этом случае мы имеем сравнение 1-й степени:  , где
, где 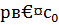 , т.е.
, т.е. 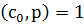 , а такое сравнение имеет в точности одно решение. Применим теперь для доказательства теоремы метод полной математической индукции.
, а такое сравнение имеет в точности одно решение. Применим теперь для доказательства теоремы метод полной математической индукции.
Предположим, что утверждение теоремы верно для всех многочленов ( 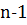 ) – й степени со старшими коэффициентами, не делящимися на простой модуль
) – й степени со старшими коэффициентами, не делящимися на простой модуль  . Возьмем теперь произвольный многочлен – й степени:
. Возьмем теперь произвольный многочлен – й степени:
 ,
,
где 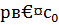 , и рассмотрим сравнение
, и рассмотрим сравнение
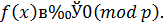
| (3.19) |
Если это сравнение не имеет ни одного решения, то число решений меньше чем  .
.
Если же это сравнение имеет решения, то возьмем любое число  , удовлетворяющее ему, и разделим
, удовлетворяющее ему, и разделим  на
на 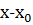 . Согласно теореме Безу будем иметь:
. Согласно теореме Безу будем иметь:
 .
.
Коэффициенты многочлена 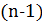 -й степени
-й степени 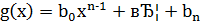 могут быть найдены по схеме Горнера и представляют собой целые числа, причем
могут быть найдены по схеме Горнера и представляют собой целые числа, причем 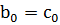 .
.
Поскольку  удовлетворяет сравнению (3.19),
удовлетворяет сравнению (3.19),  , то все решения (3,19) находятся среди решений сравнений
, то все решения (3,19) находятся среди решений сравнений  и
и  , удовлетворяя либо одному из них, либо обоим.
, удовлетворяя либо одному из них, либо обоим.
Сравнение  имеет одно решение, а сравнение
имеет одно решение, а сравнение 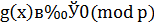 представляет собой сравнение (
представляет собой сравнение ( 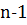 ) – й степени по простому модулю с коэффициентом при старшем члене
) – й степени по простому модулю с коэффициентом при старшем члене 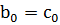 , не делящемся на
, не делящемся на  , и, по предположению, может иметь не больше чем
, и, по предположению, может иметь не больше чем 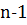 решений. Таким образом, сравнение (5) имеет не больше, чем
решений. Таким образом, сравнение (5) имеет не больше, чем 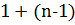 , т.е. не больше чем
, т.е. не больше чем  решений.
решений.
Согласно принципу математической индукции справедливость теоремы доказана.
Пример 4. 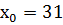 удовлетворяет сравнению
удовлетворяет сравнению  Найти все решения этого сравнения.
Найти все решения этого сравнения.
Очевидно, что вместе с классом 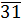 этому сравнению удовлетворяет и класс
этому сравнению удовлетворяет и класс  . Коэффициент при старшем члене
. Коэффициент при старшем члене  не делится на простой модуль
не делится на простой модуль 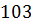 , поэтому сравнение не может иметь больше двух решений.
, поэтому сравнение не может иметь больше двух решений.
Ответ. 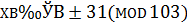 .
.
Для составных модулей эта теорема неверна. Сравнение степени  по составному модулю с коэффициентом при старшем члене, не делящемся на модуль или даже взаимно простом с модулем, может иметь больше чем
по составному модулю с коэффициентом при старшем члене, не делящемся на модуль или даже взаимно простом с модулем, может иметь больше чем  решений. Например, сравнение
решений. Например, сравнение  имеет 4 решения:
имеет 4 решения:  .
.
Теорема 6.Если сравнение степени  по простому модулю
по простому модулю  имеет больше чем
имеет больше чем  решений, то все коэффициенты сравнения делятся на
решений, то все коэффициенты сравнения делятся на  .
.
Доказательство. Возьмем любое простое число  . Если сравнение
. Если сравнение  имеет больше чем одно решение, то
имеет больше чем одно решение, то  , т.е.
, т.е.  . Таким образом, при
. Таким образом, при 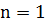 теорема верна. Предположим, что утверждение теоремы верно для многочленов степени, меньшей чем
теорема верна. Предположим, что утверждение теоремы верно для многочленов степени, меньшей чем  , т.е. предположим, что число решений сравнения степени, меньшей чем
, т.е. предположим, что число решений сравнения степени, меньшей чем  , может превосходить степень сравнения только тогда, когда все коэффициенты делятся на модуль
, может превосходить степень сравнения только тогда, когда все коэффициенты делятся на модуль  .
.
Возьмем любое сравнение степени  :
:

| (3.20) |
имеющее больше чем  решений. В таком сравнении
решений. В таком сравнении 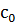 делится на
делится на  , а тогда сравнение
, а тогда сравнение

| (3.21) |
эквивалентное сравнению (3.20), также имеет больше чем  решений.
решений.
В сравнении (3.21), степень которого меньше чем  , а число решений превосходит степень согласно предположению, все коэффициенты должны делиться на
, а число решений превосходит степень согласно предположению, все коэффициенты должны делиться на  , т.е.
, т.е.  . Поскольку уже раньше было установлено, что
. Поскольку уже раньше было установлено, что  , утверждение теоремы верно для
, утверждение теоремы верно для  . Согласно принципу математической индукции справедливость теоремы доказана.
. Согласно принципу математической индукции справедливость теоремы доказана.
Теорема 7.Пусть  многочлен с целыми коэффициентами и свободным членом
многочлен с целыми коэффициентами и свободным членом  , где
, где  простое число, причем
простое число, причем 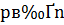 . Сравнение
. Сравнение 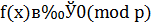 имеет
имеет  решений тогда и только тогда, когда все коэффициенты остатка от деления
решений тогда и только тогда, когда все коэффициенты остатка от деления 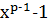 на
на  кратны
кратны  .
.
Доказательство. Пусть 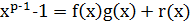 , где
, где 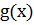 и
и 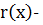 многочлены с целыми коэффициентами, причем степень
многочлены с целыми коэффициентами, причем степень 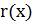 меньше чем
меньше чем  .
.
1) Докажем достаточность условия. Пусть коэффициенты 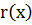 делятся на
делятся на  .
.
Обозначим через 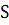 и
и 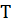 соответственно число решений сравнений
соответственно число решений сравнений
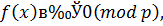
| (3.22) |

| (3.23) |
Сравнение 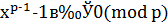 по теореме Ферма имеет
по теореме Ферма имеет 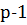 решений. Каждое из этих
решений. Каждое из этих 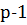 решений является решением хотя бы одного из сравнений: (3.22) или (3.23), т.е.
решений является решением хотя бы одного из сравнений: (3.22) или (3.23), т.е. 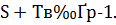
Сравнение (3.23) степени  имеет коэффициент при старшем члене, равный единице, так что
имеет коэффициент при старшем члене, равный единице, так что 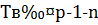 и, следовательно,
и, следовательно,
 .
.
Поскольку при этом  , получаем
, получаем 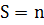 , т.е. из делимости коэффициентов
, т.е. из делимости коэффициентов 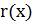 на
на  следует, что число решений сравнения (3.22) равно
следует, что число решений сравнения (3.22) равно  .
.
2) Докажем необходимость условия. Пусть сравнение (3.22) имеет  решений. Если
решений. Если  решение сравнения (3.22), то
решение сравнения (3.22), то  и вместе с тем, поскольку
и вместе с тем, поскольку  , то
, то 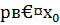 , а, следовательно, согласно теореме Ферма,
, а, следовательно, согласно теореме Ферма,  , так что
, так что
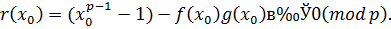
Таким образом, каждое из  решений сравнения (3.22) является решением сравнения
решений сравнения (3.22) является решением сравнения 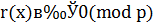 , степень которого меньше чем
, степень которого меньше чем  . Следовательно, все коэффициенты
. Следовательно, все коэффициенты 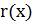 делятся на
делятся на  .
.
Пример 5. Сравнению 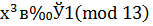 удовлетворяют классы
удовлетворяют классы 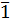 и
и  . Имеет ли это сравнение еще одно решение?
. Имеет ли это сравнение еще одно решение?
Делим 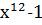 на
на 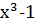 , находим:
, находим: 
так что  и, следовательно, это сравнение имеет три решения.
и, следовательно, это сравнение имеет три решения.
|
из
5.00
|
Обсуждение в статье: Сравнения по простому модулю с одним неизвестным |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

