Теория правильности расчета силового расчета

Расхождение результатов

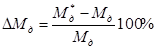
 3. Синтез зубчатой передачи

3.1 Исходные данные для проектирования зубчатой передачи

Исходные данные для проектирования зубчатой передачи приведены в табл. 1.1, а именно :

          Число зубьев первого колеса --------------------- z₁ = 10

          Число зубьев второго колеса ---------------------- z₂ = 20

       Модуль зубчатих колес z₁ и z₂ ------------------ m = 10 (мм)

3.2 Параметры исходного производящего контура

Образование боковых поверхностей зубьев колес осуществляют методами обработки металлов резанием, давлением (прокатка, штамповка) или путем отливки. Наиболее, распространенным яв­ляется зубонарезание на станках методом огибания. В этом слу­чае режущие кромки лезвийного инструмента в процессе главного движения резания образуют воображаемую поверхность, которая в относительном движении с заготовкой (движении огибания) яв­ляется огибающей для обрабатываемой поверхности зуба. Такую воображаемую поверхность называют производящей поверхно­стью. Воображаемое зубчатое колесо, у которого боковыми по­верхностями зубьев являются производящие поверхности, называ­ют производящим зубчатым колесом, а его контур в сечении — производящим контуром.

Контур зубьев производящей рейки в сечении плоскостью, перпендикулярной ее делительной плоскости, называют исходным производящим контуром (ИПК). В зависимо­сти от расположения сечения относительно линии зуба различают торцовый, осевой и нормальный исходные производящие контуры исходным производящим контуром .При про­фильной модификации поверхности зуба, в результате которой но­минальный профиль зуба начинает в заданной точке отклоняться от теоретического профиля с монотонным возрастанием отклоне­ния по мере удаления от этой точки к вершине зуба (модифика­ция головки) или к основанию зуба (модификация ножки).

Применение профильной модификации головки заключается в небольшом изменении профиля за счет его срезания в верхней ча­сти зуба. Оно необходимо для устранения кромочного зацепления, ударов заклинивания и уменьшения шума при работе, обусловленных изгибом зубьев под нагрузкой, а также отклонениями э шаге зубьев из-за неточностей при зубонарезании.

Зубчатое зацепление производящего колеса с обрабатываемым зубчатым колесом называют станочным зацеплением.

Параметры исходного контура эвольвентой цилиндрической передачи согласно ГОСТ 13755-81 :

   Коэффициент радиального зазора--------------- С ^* = 0,25

   Коэффициент высоты головки зуба -------------

  Угол главного профиля -----------------------------

   Коэффициент граничной высоты ----------------

   Коэффициент глубины захода --------------------

  Для прямозубого колеса с моду­лем m = 10 мм принимают мм/м. В отличие от высотных размеров, которые одинаковы для тор­цового и нормального исходных профилей, шаговые и угловые размеры отличаются и это следует учитывать при вычерчивании исходным производящим контуром.

Шаг зубьев по делительной прямой исходным производящим контуром для прямозубых ко­лес р = π * m.

Радиус кривизны ρ _f переходной кривой зуба ρ _f = 0,38 * m , для нормального исходного контура. Прямая, разделяющая зуб по высоте на две равные части, называются делительной. На исходным производящим контуром отмечаются еще четыре линии, параллельные делительной прямой и проходящие по основаниям впадин зубьев, по их вершинам и через точки сопряжения прямолинейной часта зуба дугами радиусов ρ _f .

С помощью исходным производящим контуром представляется возможным нарезать как нулевые, так и исправленные ( корригированные ) колеса.

При нарезании нулевого колеса делительная прямая исходным производящим контуром касается делительной окружности колеса. При нарезании корригированного колеса с положительным смещением она отодвинута от делительной окружности - от оси вращения колеса на величину, равную хm, где х - коэффициент смещения. При нарезании отрицательного колеса длительная прямая исходным производящим контуром придвинута к центру колеса на величину отрицательного смещения, равного – хm .

3.3 Выбор коэффициента смещения

Положение исходного производящего контура относительно делительной окружности проектируемого зубчатого колеса оказывает влияние на форму профиля зуба в торцовом сече­нии, следовательно, и на эксплуатационные свойства проек­тируемого зацепления. За нулевое смещение принимают такое положение исходного производящего контура, при котором его делительная прямая касается делительной окружности зубчатого колеса.

Расстояние по нормали между делительной прямой исходного производящего контура и делительной окружностью колеса называют смещением, а отношение величины смещения к расчетному модулю называют  коэффициентом смещения и обозначают буквой x. Расчетный модуль m — линейная величина, в π раз меньшая нормального шага зубьев по делительной окружности. Коэффициент смеще­ ния — величина безразмерная, но имеет знак: х >0, если дели­тельная прямая исходного производящего контура располагается вне делительной окружности нарезаемого колеса, т. е. смещение осуществляют в сторону увеличения станочного расстояния, и x < 0, если при смещении делительная прямая исходного производящего контура  пересекает делительную окружность зубчатого колеса. Коэффициенту смещения x приписывают ин­дексы: 1 — для шестерни x_{1 ,} 2 — для колеса х₂.

Коэффициент смещения влияет на форму зу­ба, который может оказаться в пределе подрезанным или заостренным. Предельные значения коэффициента сме­щения, соответствующие на­именьшему и наибольшему смещениям исходного произ­водящего контура, обознача­ет: х _min , х_max — коэффициент наименьшего смещения ис­ходного контура, при кото­ром отсутствует геометрическое заострение зуба.

Расчетное значение коэффициента смещения х должно быть в пределах: х _min≤ х ≤ х_∆ . = 0,5                                                         

Для ориентировочного выбора коэф­фициентов смещения на рис.1 приведены графики x(z), ограни­чивающие область, в которой не наблюдается ни подреза зуба (граничная линия 1), ни заострения вершины (граничная линия 2).

3.4 Расчет геометрических параметров зубчатой передачи

Вычислениях проводить в такой последовательности:

1.       Коэффициент  суммы смещений:

          

где :

        - коэффициент смещения при числе зубьев z₁= 10

        - коэффициент смещения при числе зубьев z₁= 20

2. Угол зацепления :

                                                                       

Угол  находят по таблицам эвольвентой функции (см. При­ложение III (Попов С.А. « Курсовое проектирование »)) = 27.2

3. Межосевое расстояние а_w:

                ( мм )

4. Делительные диаметры  и :

                                           (мм)

                                               (мм)

5. Делительное межосевое расстояние а :

                                       (мм)

6. Коэффициент воспринимаемого смещения y :

     

 7. Коэффициент уравнительного смещения ∆ у :

   

8. Радиусы начальных окружностей и :

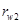                (мм)

                 (мм)

Проверка вычислений:

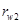         =  +  = 52.826+105.653=158.479              (мм)   

9. Радиусы вершин зубьев  и :

        (мм)

      (мм)

10. Радиусы впадин  и :

             (мм)

          (мм)   

11. Высота зуба h :

              (мм)   

12. Толщины зубьев по делительной окружности S₁ и S₂ :

               ( мм)

                 ( мм)

13. Радиусы основных окружностей:
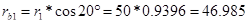                           ( мм)

                            ( мм)

15. Шаг р:

                                    (мм)

Учитывая, что коэффициент для построения , занесем данные в таблицу 1.12

                                                               Таблица 1.12

Наименование	Обозначение	Единицы измерения	Расчетные данные
Межосевое расстояние		мм	158.479	500
Радиусы начальных окружностей		мм	52.826	166.667
			105.653	333.333
Радиусы основных окружностей		мм	46.985	148.236
			93.969	296.472
Радиусы вершин зубьев		мм	63.479	200.276
			113.479	358.025
Радиусы впадин		мм	42.5	134.087
			92.5	291.837
Высота зуба	h	мм	20.979	66.189
Шаг	р	мм	31.416	99.117

3.5 Вычерчивание картины эвольвентного зацепления

Для построения картины эвольвентного зацепления выбираем масштабный коэффициент из расчета, чтобы центры обоих колес находились на чертеже, а межосевая линия располагалась горизонтально. Откладываем межосевое расстояние, проводим начальные, делительные, основные окружности, а также окружности вершин и впадин колес. Проводим касательную к основным окружностям. Точки касания с основными окружностями обозначены N₁ и N₂. Отрезок N₁П разделим на 4 равных участка. За точкой N₁ влево по линии зацепления откладываем два таких же участка. По дуге основной окружности вправо от точки N₁ откладываем дуги, равные отрезкам 1П , 12 и т.д. От точки N₁ влево по основной окружности откладываем две дуги, равные вышеназванным отрезкам. От точек 1,2 и т.д. проводим касательные к основной окружности, на которых откладываем соответствующее количество участков. Соединяем отрезки на касательных с помощью лекала и получаем эвольвенту, которая будет правым профилем зуба первого колеса.

       От точки пересечения эвольвенты с делительной окружностью по дуге этой окружности откладываем влево половину толщины зуба. Через конец этой дуги проводим осевую линию зуба, соединив с осью первого колеса. Участок профиля между основной окружностью и окружностью впадин выполнен прямой линией, параллельной оси симметрии зуба. Галтель выполнен дугой окружности.

       Затем строим левую половину зуба с помощью шаблона (или по закону симметрии). Проводим оси симметрии двух соединенных зубьев. Отложив от точки пересечения оси первого зуба с делительной окружностью влево и вправо шаг Р колеса. С помощью шаблона строим соединенные зубья или по закону симметрии.        Далее на чертеже выделяем активную часть линии зацепления, рабочие участки А₁В₁ и А₂В₂ профилей зубьев ( на чертеже показаны в виде заштрихованных полосок).

По данным таблицы 3.1 строим графики изменения коэффициентов относительного скольжения в зависимости от изменения положения точки К контакта сопряженных профилей на линии зацепления. За начало координат принимаем точку П – полюс зацепления. Положительное направление оси абсцисс графика  совпадает с направлением перемещения точки контакта профилей при ведущем колесе 1.

3.6 Показатели качества работы зубчатой передачи

3.6.1 Коэффициент перекрытия

К качественным показателям относятся коэффициент перекрытия и коэффициент относительного скольжения зубьев, коэффициент удельного давления, а также некоторые другие коэффициенты, которые в курсах теории механизмов и прикладной механике не рассматриваются.

Качественные показатели позволяют оценивать плавность, бесшумность, прочность, возможный износ зубьев колес передачи при ее проектировании, и сравнить ее с другими передачами по тем же показателям. Такая оценка важна для рационального выбора смещений исходным производящим контуром при проектировании.

Коэффициент перекрытия, ξ _а позволяет оценить плавность и непрерывность зацепления. Для плавной безударной работы передачи необходимо, чтобы каждая последующая пара зубьев входила в зацепление до того, как предыдущая пара выйдет из него. Величина перекрытия характеризуется коэффициентом перекрытия, выражающим отношение угла зацепления к угловому шагу зубчатого колеса и определяется по формуле :

+

+ 0, 44 2 + 0, 725 = 1 .167

Проверяем активную линию зацепления по формуле:

Коэффициент перекрытия показывает, сколько пар профилей зубьев, попеременно участвуют в зацеплении. Для нормальной работы прямозубой передачи коэффициент перекрытия должен быть больше 1.

При  ≥ 1.15 15% всего времени работы передачи в зацеплении находятся 2 пары профилей зубьев, а 85% времени работы -1 пара профилей зубьев, т.е. в зацеплении попеременно находятся то 2 пары профилей зубьев, то 1 пара.

3.6.2 Коэффициент удельного и относительного скольжения профилей

Степень вредного влияния скольжения профилей в процессе работы характеризуется коэффициентами относительного скольжения зубьев. Коэффициенты относительного скольжения зубьев учитывают влияние геометрических и кинематических факторов на величину относительного проскальзывания профилей в процессе зацепления. Наличие скольжения и давление одного профиля на другой при передаче усилий приводит к износу профилей. В зубчатой передаче необходимо учитывать, что зубья большого колеса находятся в зацеплении в U_{1 2} раза меньше, чем зубья шестерни. Коэффициенты относительного скольжения зубьев определяются по формулам :
                     ( мм )

                     ( мм )

 

   где :   - расстояние от полюса зацепления до точки контакта пары зубьев ;

 и    - расстояние от точек касания линии зацепления с основными окружностями соответственно шестерни и колеса до полюса.

Из этих формул следует, что с удалением точки контакта профилей от полюса, коэффициенты скольжения возрастают, причем интенсивно на ножках зубьев. В инженерной практике о качестве передачи принято судить по максимальным значениям коэффициентов скольжения на ножках зубьев, которые соответствуют входу и выходу пары зубьев из зацепления.

Данн ые расчета заносим в таблицу (1.13)

Таблица коэффициентов относительного скольжения зубьев

Таблица 1.13

На иминование	Размерность	Длина
Lpk	мм	84	56		28		0	25		50		75
LpN1	мм	108
LpN 2	мм	112
λ 1	-	6,1 365		3, 6 652		2, 5 668	0		1,6296		1,3968		1,2416
λ 2	-	5,87243		3,50452		2,49747	0		1,585985		1,341235		1,161925
	мм	67 ,058		30 ,10903		22 ,16014	0		13,88075		11,89779		10,57581
	мм	50,0207		29,85111		21,27317	0		13,50924		11,42449		9,897147

Масштабный коэффициент для построения графика относительного скольжения зубьев определяем по формуле :   

Коэффициент удельного давления θ учитывает влияние радиусов кривизны профилей зубьев на значаще контактных напряжений. За расчетный коэффициент удельного давления принимают такой, который соответствует контакту зубьев в полюсе зацепления, т. к. при прямозубом зацеплении в полюсе чаще всего контактирует только одна пара профилей зубьев. Значение коэффициента удельного давления в полюсе рассчитывают по формуле :