Лабораторная работа №5

ИСПОЛЬЗОВАНИЕ ФИНАНСОВЫХ ФУНКЦИЙ ДЛЯ РАСЧЕТА АМОРТИЗАЦИИ ОСНОВНЫХ СРЕДСТВ

Цель работы: изучить финансовые функции АСЧ, АПЛ, ДДОБ, ПУО, ФУО.

    Для определения величины амортизации актива необходимо знать первоначальную стоимость актива, срок его эксплуатации и остаточную стоимость актива. Величина амортизации определяется по одному из общепринятых методов начисления амортизации.

    B EXSEL имеется пять функций для вычисления величины амортизации.

    Функция АПЛ вычисляет величину амортизации по линейному методу;

    Функция АСЧ использует метод «суммы (годовых) чисел» для вычисления суммы амортизации; функции ДДОБ и ПУО используют метод ускоренного начисления амортизации; функция ФУО вычисляет величину амортизации методом фиксированного уменьшения остатка.

    Задача №1

    Стоимость актива составляет 10 000 руб., срок эксплуатации актива – 5 лет, а ликвидационная стоимость – 2000 рублей. Создать таблицу начисления износа, в которой бы указывались суммы ежегодной амортизации значения остаточных стоимостей в конце каждого года, применяя один из методов начисления амортизации:

линейный метод;

суммы (годовых) чисел;

фиксированного уменьшения остатка;

двойного уменьшаемого остатка;

двойного процента со снижающего остатка.

Ход работы

    1. Для того чтобы решить задачу с использованием линейного метода начисления амортизации, необходимо использовать функцию АПЛ.

    Функция АПЛ возвращает величину амортизации актива за один период, рассчитанную линейным методом. Линейный метод еще называют методом равномерного начисления износа. Он заключается в том, что из суммы стоимости актива вычитается его остаточная стоимость; полученное значение делится на количество лет эксплуатации. Таким образом, величина амортизации на протяжении всего периода эксплуатации актива постоянна (Рис.5.1.).

Рис.5.1.Исходные данные и решение задачи с использованием функции АПЛ

    Функция АПЛ имеет следующий синтаксис:

АПЛ (нач_стоимость; ост_стоимость; время_эксплуатации).

Аргумент нач_стоимость – это первоначальная стоимость актива.

 Аргумент ост_стоимость – это остаточная стоимость актива.

Аргумент время_эксплуатации – это период амортизации или срок эксплуатации актива.

    На рис.5.1.(ячейки В9;В13) приведен расчет величины амортизации за каждый период по формуле =АПЛ($D$3;$D$4;$D$5).

    Остаточная стоимость актива определяется как разность между первоначальной стоимостью и величиной амортизации, начисленной за предыдущие периоды.

    В конце первого года эксплуатации остаточная стоимость актива вычисляется по формуле 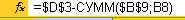; в конце второго 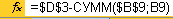; в конце третьего ; в конце четвертого ; в конце пятого .

    Как видно из рис.5.1. уменьшение остаточной стоимости актива происходит по линейному закону.

    2. Чтобы решить задачу с использованием метода «суммы ( годовых) чисел», необходимо использовать функцию АСЧ.

    Функция АСЧ возвращает величину амортизации актива за данный период, рассчитанную методом «суммы (годовых) чисел». В этом методе суммируются порядковые номера лет, в течение которых актив находится в эксплуатации.(Рис.5.2.)

Рис.5.2. Исходные данные и решение задачи с использованием функции АСЧ

    Синтаксис функции АСЧ имеет следующий вид:

АСЧ (нач_стоимость;ост_стоимость;время_эксплуатации;период)

Аргументы нач_стоимость и ост_стоимость- это соответственно первоначальная и остаточная стоимость актива. Аргумент время_эксплуатации- это период амортизации актива или полный срок его эксплуатации. Аргумент период – это текущий период.

    На рис.5.2. величина амортизации за первый период (ячейка В9) вычисляется по формуле .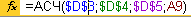

    Чтобы вычислить величину амортизации за другие периоды, скопируем эту формулу в ячейке В10;В13. Остаточная стоимость актива определяется как разность между первоначальной стоимостью и величиной амортизации, начисленной за предыдущие периоды.

    В конце первого года эксплуатации остаточная стоимость актива вычисляется по формуле , в конце второго , в конце третьего , в конце четвертого 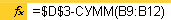, в конце пятого . В конце срока эксплуатации актива его стоимость становится равной остаточной стоимости. Ячейка С13 возвращает остаточную стоимость актива.

    3. Чтобы решить задачу с использованием метода фиксированного уменьшения остатка, необходимо использовать функцию ФУО.

    Функция ФУО возвращает величину амортизации актива для заданного периода, рассчитанную методом фиксированного уменьшения остатка или методом уменьшающего баланса. Амортизация по данному методу начисляется каждый год на основе фиксированной процентной ставки.

    При вычислении амортизации по методу фиксированного уменьшения остатка используется значение суммарной амортизации за предшествующие периоды (рис.5.3.).

Рис.5.3. Использование функции ФУО для решения задачи

    Величина амортизации за текущий период вычисляется как разность между первоначальной стоимостью актива и суммарной амортизацией за предшествующие периоды, умноженная на фиксированную процентную ставку, которая вычисляется по формуле Ставка = 1- ((остаточная стоимость /первоначальная стоимость)(1/время эксплуатации)).

    Функция ФУО имеет следующий синтаксис:

ФУО(нач_стоимость;ост_стоимость;время_ эксплуатации;период;месяцы).

Аргументы нач_стоимость и ост_стоимость- это соответственно первоначальная и остаточная стоимость актива. Аргумент время_ эксплуатации – это период амортизации актива или полный срок его службы. Аргумент период- это текущий период, для которого необходимо вычислить величину амортизации. Последний аргумент месяцы задает количество месяцев первого года. Этот аргумент является необязательным и его следует задавать только в том случае, когда покупка актива была совершена не в начале года, а позже. По умолчанию значение этого аргумента принимается равным 12.

    На рис.5.3. величина амортизации за первый период (ячейка В9) вычисляется по формуле . Чтобы найти величину амортизации за другие периоды, скопируем эту формулу в диапазон В10;В13.

              В конце первого года эксплуатации остаточная стоимость актива вычисляется по формуле , в конце второго , в конце третьего , в конце четвертого 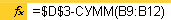, в конце пятого .

    Обратим внимание, что остаточная стоимость актива в ячейке С13 на 3 рубля больше, чем остаточная стоимость, определенная ранее (на рис.5.3. точное значение остаточной стоимости содержится в ячейке D4). Так получилось потому, что фиксированная ставка, которую вычисляет функция ФУО, округляется до трех цифр, т.е. вместо значения 0,27522…, вычисленного по формуле , в вычислениях используется ставка 0,275.

    Использование аргумента месяцы функции ФУО при вычислении величины амортизации актива позволяет учесть время покупки актива. Так, если покупка сделана не в январе, а например, в июне, то для вычисления величины амортизации за первый год необходимо использовать следующую формулу: .

    В качестве аргумента месяцы функции ФУО используется число 6, определяющее количество месяцев, в течение которых будет начисляться амортизация в первый год. Для того чтобы вычислить величину амортизации за другие периоды скопируем эту формулу в ячейки В10;В14 (рис.5.4.).

    Период начисления амортизации начинается в середине первого года и заканчивается в середине шестого года. Поэтому на рис.5.4. указаны шесть периодов.

Рис.5.4. Использование функции ФУО для вычисления величины амортизации актива (за неполный первый год).

    4. Чтобы решить задачу с использованием метода двойного уменьшаемого остатка, необходимо использовать функцию ДДОБ.

    Функция ДДОБ возвращает величину амортизации актива за данный период, рассчитанную по методу двойного уменьшаемого остатка. При начислении амортизации по методу двойного уменьшаемого остатка коэффициент, который использовался для определения величины амортизации по линейному методу, удваивается, а затем умножается на первоначальную стоимость. После этого из полученного произведения вычитается сумма всех предыдущих величин амортизации. Можно не удваивать коэффициент при начислении амортизации, а умножить его на 1,5.

    Функция ДДОБ имеет следующий синтаксис:

ДДОБ(нач_стоимость;ост_стоимость;время_эксплуатации;период;

коэффициент)

Аргументы нач_стоимость и ост_стоимость –это первоначальная и остаточная стоимости актива. Аргумент период – это текущий период, для которого требуется вычислить амортизацию. Аргумент коэффициент определяет процентную ставку. Если этот аргумент опущен, то он полагается равным 2. В этом случае используется метод удвоенного уменьшаемого остатка.

Рис.5.5. Использование функции ДДОБ для решения задачи

    На рис.5.5. приведен пример вычисления амортизации по методу двойного уменьшаемого остатка В10:В13.

    Величина амортизации в первый период вычисляется по формуле . Чтобы вычислить величину амортизации в последующие периоды, скопируем эту формулу в ячейки.

    Данный метод позволяет значительно ускорить процесс начисления амортизации. Вместо коэффициента 2 можно использовать другое значение. Например, чтобы увеличить величину амортизации в 1,5 раза, то введем в ячейку В9 формулу  и скопируем ее в ячейки В10:В13.

    5.Чтобы решить задачу с использованием метода двойного процента со снижающего остатка, необходимо использовать функцию ПУО.

    Функция ПУО возвращает величину амортизации актива за данный период, используя метод двойного процента со снижающего остатка.

    Синтаксис функции ПУО имеет следующий вид:

    ПУО(нач_стоимость;ост_стоимость;время_эксплуатации;нач_период; кон_период; коэффициент; без_переключения)

    Аргументы нач_стоимость и ост_стоимость- это соответственно начальная и остаточная стоимость актива, аргумент время_эксплуатации- это полный срок службы актива. Аргументы нач_период и кон_период задают начальный и конечный периоды, для которых необходимо вычислить величину амортизации. Например, для первого года эксплуатации актива аргумент нач_период равен 0, а аргумент кон_период -1. Если необходимо вычислить величину амортизации за первое полугодие первого года эксплуатации, то значения аргументов нач_период и кон_период соответственно равны 0 и 0,5.Аргумент коэффициент - это процентная ставка снижающего остатка.Если этот аргумент опущен, то он полагается равным 2. В этом случае функция ПУО возвращает ту же величину амортизации, что и функция ДДОБ с аргументом коэффициент, равным 2. Если необходимо использовать другой метод начисления амортизации, укажем нужное значение аргумента коэффициент.

Рис.5.6. Решение задачи с использованием функции ПУО.

         Аргумент без_переключения имеет значение ИСТИНА

        В конце первого года эксплуатации остаточная стоимость актива вычисляется по формуле , в конце второго , в конце третьего , в конце четвертого 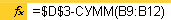, в конце пятого .

    На рис.5.6. приведен пример начисления амортизации с использованием функции ПУО, у которой аргумент коэффициент равен 1, а аргумент без_переключения имеет значение ИСТИНА. Обратим внимание, что к концу срока эксплуатации актива его первоначальная стоимость не уменьшается до остаточной стоимости. Чтобы этого не было, следует использовать другое значение аргумента Коэффициент либо присвоить аргументу без_переключения значение ЛОЖЬ.

    Последний аргумент без_переключения определяет метод расчета амортизации. Если аргумент без_переключения имеет значение ЛОЖЬ или опущен, функция ПУО переключается на линейный метод начисления амортизации; но переключение на линейный метод выполняется только в том случае, если начисление амортизации по линейному методу происходит быстрее, чем по методу двойного процента со снижающего остатка. Если аргумент без_переключения имеет значение истина, то функция ПУО не переключается на линейный метод начисления линейной амортизации.

    На рс.5.7. аргумент без_переключения функции ПУО имеет значение ЛОЖЬ. В этом случае происходит переключение на линейный метод начисление амортизации. Как следствие, к концу пятого года эксплуатации актив полностью изношен.

Рис.5.7. Решение задачи с использованием функции ПУО.

Аргумент без_переключения имеет значение ЛОЖЬ

ВЫВОД:

При работе с финансовыми функциями ПС (приведенная стоимость);

БС (будущая стоимость); Платеж (аргумент ПЛТ) - размер одноразовой выплаты или одноразовой выплаты с процентами; СТАВКА; КПЕР;

ОСПЛТ; ПРПЛТ;ОБЩПЛАТ;ОБЩДОХОД; АСЧ; АПЛ; ДДОБ; ПУО; ФУО очень важно правильно выбрать единицу измерения для задания периода выплат, процентной ставки и срока. Три этих величины должны быть согласованы между собой.

    Также необходимо учитывать направление денежного потока. Если деньги поступают к нам, они отмечаются знаком «плюс», если отдаются нами, тогда – знак «минус».

        

 

Использованная литература:

1. М.С.Лазуткина Методическое пособие по выполнению лабораторных работ.

ДВГУПС 2009. – 52 с.