Алгоритм Краскала вычисляет для заданного взвешенного неориентированного графа G остовное дерево с наименьшей суммой весов ребер — остовное дерево наименьшего веса.

Существенное отличие только что сформулированной задачи от задачи Штейнера (в ее графовой постановке) состоит в том, что в новой задаче множество вершин при поиске остовного дерева наименьшего веса не меняется. Поэтому алгоритм Краскала и дает лишь некоторое приближение решения задачи Штейнера.

При описании алгоритма будем использовать способ хранения данных, называемый очередью. Элементы данных в очереди упорядочиваются по времени поступления. Элементы можно добавлять в очередь и извлекать из очереди.

В каждый момент времени доступен только один элемент, который был помещен в очередь раньше других, — "голова" очереди. При добавлении новый элемент помещается в "хвост" очереди, т.е. работа ведется по обычному для очереди правилу — "первым пришел — первым вышел". Чтобы извлечь из очереди некоторый элемент, не доступный в текущий момент, надо извлечь все ранее поступившие элементы, начиная с "головы" очереди.

Рассмотрим алгоритм нахождения остовного дерева наименьшего веса (алгоритм Краскала).

Пусть дан связный неориентированный граф G = (V,E)  с числовыми неотрицательными весами ребер. Вес ребра е обозначим φ(e) .

В результате работы алгоритма получим остовное дерево T = (V, H) графа G, такое, что сумма 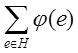 является наименьшей.

Отсортируем все ребра исходного графа по возрастанию весов и сформируем из них очередь так, чтобы в "голове" очереди находилось ребро с наименьшим весом, а в "хвосте" — с наибольшим и веса ребер не убывали от "головы" очереди к "хвосту".

Метод состоит в "сшивании" искомого дерева из компонент остовного леса. Первоначально остовный лес представляет собой множество изолированных вершин исходного графа, т.е. его множество ребер пусто.

1. На первом шаге из очереди извлекается ребро наименьшего веса и добавляется к множеству ребер исходного дерева.

2. На последующих шагах алгоритма из очереди извлекается по одному ребру. Если это ребро соединяет вершины, принадлежащие разным компонентам текущего остовного леса, то оно добавляется к текущему множеству ребер искомого дерева, а указанные компоненты сливаются в одну. Иначе ребро отбрасывается.

3. Процесс повторяется до тех пор, пока число компонент остовного леса не окажется равным 1. Можно показать, что эта компонента и будет искомым остовным деревом наименьшего веса.

Переходим к формальному описанию алгоритма Краскала.

1. Множество ребер H искомого остовного дерева полагаем пустым (H= ∅ ) .

2. Формируем множество VS={{v1},…,{vn}}, элементами которого являются

Множества вершин, соответствующих компонентам исходного остовного

Леса. Каждая такая компонента состоит из единственной вершины.

3. Сортируем множество ребер E исходного графа по возрастанию весов и

Формируем очередь Q, элементами которой являются ребра графа G.

Если множество VS содержит более одного элемента (т.е. остовный лес

Состоит из нескольких компонент) и очередь Q не пуста, переходим на шаг 5, если иначе — на шаг 7.

5. Извлекаем из очереди Q ребро e. Если концы ребра е принадлежат

Различным множествам вершин Vi и Vj из VS, то переходим на шаг 6, если иначе, то отбрасываем извлеченное ребро и возвращаемся на шаг 4.

6. Объединяем множества вершин Vi и Vj  (полагая W = Vi ∪ Vj ), удаляем

множества Vi и Vj из множества VS и добавляем в VS множество W.

Добавляем ребро e в множество H. Возвращаемся на шаг 4.

Прекращаем работу. Множество H есть множество ребер полученного

Остовного дерева.

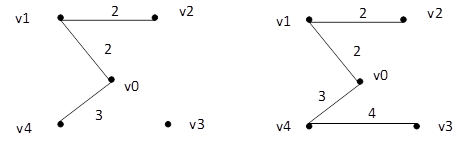
                      г)                                                д)

Рис. 3.7

На рис. 3.7 (а-д) для неориентированного графа показана последовательность построения остовного дерева наименьшего веса. Заметим, что результат работы алгоритма в общем случае зависит от порядка следования ребер одинакового веса в очереди. Предположим, что после сортировки первым в очереди находится ребро

{v0,v1} с весом 2.

Исходный граф изображен на рис. 3.7,а. На рис. 3.7,б проиллюстрирован результат выполнения первого шага алгоритма. На рис. 3.7, в показан результат добавления следующего ребра {v1,v2}с весом 2 из очереди. На рис. 3.7,г приведен результат добавления ребра {v0,v4}с весом 3. Если следующим в очереди ребром будет {v1,v4}, оно будет отброшено.

Дальнейший ход работы алгоритма зависит от того, в каком порядке в очереди размещены ребра {v2, v3} и {v3, v4} с весами 4.

 Любое из них может быть добавлено в множество ребер остовного дерева, и на этом алгоритм закончит работу. На рис. 3.7,д приведено остовное дерево, полученное после добавления ребра {v3,v4}.

Отметим, что для приведенного графа оба ребра с весом 2 войдут в остовное дерево независимо от порядка их расположения в очереди после сортировки, а ребро {v1,v4}

не войдет ни в какое остовное дерево наименьшего веса.

Наиболее трудоемким шагом в алгоритме Краскала является сортировка ребер графа по возрастанию весов.