Логические операции. СДНФ. СКНФ.

Коммутативность

x₁ & x₂ = x₂ & x_1.                                                                    

x₁ v x₂ = x₂ v x_{1 .}

Ассоциативность

x ₁ v (x₂ v x₃) = (x₁ v x₂) v x_3.

x ₁ & (x₂ & x₃) = (x₁ & x₂) & x_{3 .}

Дистрибутивность

x ₁ & (x₂ v x₃) = (x₁ & x₂) v ( x 1 & x₃ ).                                                                

x ₁ v ( x ₂ & x ₃ ) = ( x ₁ v x ₂ ) & ( x 1 v x ₃ ).

Отметим также важные соотношения:

X v X = X , X & X = X , X v 1 = 1, X & 1 = X ,

X v 0 = X , X & 0 = 0, X v Ø X = 1, X & Ø X = 0.

Положим x ^a =  { X , если a = 1; и

                             Ø X , если a = 0 } .                     

Утверждение. Любая функция алгебры логики кроме 0 может быть представлена в форме

   f(x ₁...x_n) = Ú x₁ ^a & x₂ ^a... & x_n ^a                                  (1)

При этом дизъюнкция в правой части берется только по тем наборам аргументов, на которых функция, заданная таблично, обращается в 1.

Формула (1) определяет СДНФ.

Определение. Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая дизъюнктивная нормальная форма, у которой в каждую конъюнкцию входят все переменные списка (либо сами, либо их отрицания), причём в одном и том же порядке.

Например, выражение 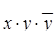  не является СДНФ, а выражение   является СДНФ для списка переменных  {x y z}.

Определение. Простой дизъюнкцией называется дизъюнкция одной или нескольких переменных, при этом каждая переменная (либо сама, либо её отрицание) входит в дизъюнкцию не более одного раза.

Например, выражение является простой дизъюнкцией.

Определение. Конъюнктивной нормальной формой (КНФ) называется конъюнкция простых дизъюнкций.

Например, выражение   является КНФ.

Пример. Приведем к КНФ логическую формулу :

F = ( X → Y ) ∧ ( ( Y → Z ) → X ) .

Преобразуем формулу    F к формуле, не содержащей → , получим:

F = ( X ∨ Y ) ∧ ( ( Y → Z ) ∨ X ) = ( X ∨ Y ) ∧ ( ( Y ∨ Z ) ∨ X ) В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания:

F = ( X ∨ Y ) ∧ ( ( Y ∧ Z ) ∨ X ) .

По закону дистрибутивности получим КНФ:

F = ( X ∨ Y ) ∧ ( X ∨ Y ) ∧ ( X ∨ Z ) . F = ( X ∨ Y ) ∧ ( X ∨ Y ) ∧ ( X ∨ Z ) . {\displaystyle F=(\neg X\vee Y)\wedge (\neg X\vee \neg Y)\wedge (\neg X\vee \neg Z).}

Определение . Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные списка (либо сами, либо их отрицания) причём в одном и том же порядке.

Например, выражение   

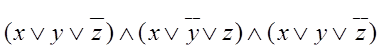        является СКНФ.

Теорема. Всякая булева функция (кроме 0) имеет единственную СДНФ.

Следствие . Всякая булева функция может быть выражена через дизъюнкцию, конъюнкцию и отрицание.

Теорема . Всякая булева функция (кроме 1) может быть единственным образом представлена в виде СКНФ.

Рассмотрим алгоритм построения СДНФ булевой функции по заданной таблице истинности.

В таблице истинности берём только те наборы переменных (x¹ , x² ,..., xⁿ ) , для которых f (x¹ , x² ,..., xⁿ) = 1 и составляем простую конъюнкцию для этого набора так: если x_i = 0 , то берём в этой конъюнкции x_i , если x_i = 1, то берём x_i . Составляя дизъюнкцию этих простых конъюнкций, придём к СДНФ.

По аналогии с представлением любой функции (не равной 0) в виде СДНФ можно любую функцию (не равную 1), представить в виде СКНФ. А именно, простые дизъюнкции составляются для тех наборов переменных

(x¹ , x² ,..., xⁿ), для которых f ( x¹ , x² ,..., xⁿ ) = 0, причём если в наборе xⁱ = 1, то в простую дизъюнкцию включаем xi , если же xⁱ = 0 , то в неё включаем xⁱ .

Пример.  Составим СДНФ и СКНФ для импликации и сложения по модулю два.

Решение.

СДНФ для этих функций имеет вид:

СКНФ для этих функций будет иметь вид: