 |
Главная |
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
|
из
5.00
|
1. Элементы комбинаторики Размещением с повторениями из n по m элементов называется конечная последовательность 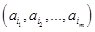 элементов некоторого множества
элементов некоторого множества  . Если все члены выборки различны, то последовательность называется размещением без повторений. Размещения без повторения - m -элементные выборки, различающиеся либо входящими элементами, либо порядком их следования. Размещение с повторениями – это выборка с возвращением выбираемых элементов. Число всех возможных размещений с повторениями равно
. Если все члены выборки различны, то последовательность называется размещением без повторений. Размещения без повторения - m -элементные выборки, различающиеся либо входящими элементами, либо порядком их следования. Размещение с повторениями – это выборка с возвращением выбираемых элементов. Число всех возможных размещений с повторениями равно  (число комбинаций, выбираемых из m групп, содержащих по n элементов). Размещение без повторения – выборка без возвращения выбираемых элементов . Общее число различных комбинаций – размещений без повторений обозначается символом
(число комбинаций, выбираемых из m групп, содержащих по n элементов). Размещение без повторения – выборка без возвращения выбираемых элементов . Общее число различных комбинаций – размещений без повторений обозначается символом  и равно
и равно  (количество выборок из m групп, содержащих соответственно
(количество выборок из m групп, содержащих соответственно  ,
,  , …,
, …,  элементов).
элементов).
Перестановками называются размещения из n по n элементов. Общее число перестановок обозначают символом  .
.
Сочетаниями из n по m элементов называются m - элементные подмножества множества  , имеющие различный состав элементов. Два сочетания считаются различными, если хотя бы один элемент входит в одну комбинацию, но не входит в другую. Общее число различных сочетаний обозначают символом
, имеющие различный состав элементов. Два сочетания считаются различными, если хотя бы один элемент входит в одну комбинацию, но не входит в другую. Общее число различных сочетаний обозначают символом  .
.
Число размещений, перестановок и сочетаний определяются формулами:

2. Классическое определение вероятности
 , где n – общее число элементарных событий (исходов, которые в данном опыте образуют конечную полную группу равновозможных попарно несовместных событий), m – число элементарных событий, благоприятствующих наступлению события А.
, где n – общее число элементарных событий (исходов, которые в данном опыте образуют конечную полную группу равновозможных попарно несовместных событий), m – число элементарных событий, благоприятствующих наступлению события А.
3. Геометрическое определение вероятности
 . Вероятность попадания точки в какую либо часть А области Ω пропорциональна мере (длине, площади, объему и т.д.) этой части и не зависит от ее расположения и формы.
. Вероятность попадания точки в какую либо часть А области Ω пропорциональна мере (длине, площади, объему и т.д.) этой части и не зависит от ее расположения и формы.
4. Основные свойства вероятности
Вероятность любого события А - число, заключенное между 0 и 1. Вероятность невозможного события равна 0. Вероятность достоверного события равна 1.
Сумма вероятностей противоположных событий равна 1:

Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:

Для любых двух событий A и B имеет место формула (теорема сложения для произвольных событий):
 .
.
Для полной группы несовместных событий 

Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:
 - теорема умножения.
- теорема умножения.
Если события А и В – независимые, то
 - теорема умножения.
- теорема умножения.
5. Формула полной вероятности. Формулы Байеса
Если известно, что событие А может произойти с одним из событий  (гипотез), образующих полную группу попарно несовместных событий, то вероятность события А определяется по формуле полной вероятности:
(гипотез), образующих полную группу попарно несовместных событий, то вероятность события А определяется по формуле полной вероятности:

Вероятности гипотез после того как имело место событие А переоценивают по формулам Байеса:

Пример . В ящике находится 10 деталей. Из них 3 дефектные. Наудачу отобраны 3 детали. Какова вероятность того, что:
а) все детали дефектные (событие А);
б) только одна деталь дефектная (событие В);
в) все три детали годные (событие С);
г) хотя бы одна деталь дефектная (событие D ).
Решение. Используем классическое определение вероятности.
а) Событие А = {выбранные три детали дефектные};

Элементарное событие в данной задаче - комбинация (сочетание) из трех деталей.  - общее число способов выбрать 3
- общее число способов выбрать 3  детали из имеющихся 10 деталей.
детали из имеющихся 10 деталей.
 (имеется всего один вариант выбора 3 дефектных деталей).
(имеется всего один вариант выбора 3 дефектных деталей).
 .
.
б) Событие В = {из трех выбранных деталей 1 деталь дефектная, две детали без дефекта};
 ,
,
где  - количество вариантов, благоприятствующих появлению события В, при которых 1 дефектная деталь выбирается из группы 3 дефектных и 2 бездефектные детали выбираются из группы 7 бездефектных деталей
- количество вариантов, благоприятствующих появлению события В, при которых 1 дефектная деталь выбирается из группы 3 дефектных и 2 бездефектные детали выбираются из группы 7 бездефектных деталей 
Следовательно, 
в) Событие С = {выбранные три детали бездефектные}

г) Событие D = {хотя бы одна из трех выбранных деталей бездефектная}. Рассмотрим противоположное событие 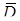 .
.
 = { среди трех выбранных деталей нет дефектных}. Так как
= { среди трех выбранных деталей нет дефектных}. Так как  , то
, то 
Пример . В ящике лежат 20 теннисных мячей, в том числе 15 новых и 5 игранных. Для игры наудачу выбираются два мяча и после игры возвращаются обратно. Затем для второй игры также наудачу извлекается ещё 2 мяча. Какова вероятность того, что вторая игра будет проводиться новыми мячами?
Решение. Рассмотрим предположения (гипотезы):
Н1={на первую игру выбирают два новых мяча}.
Н2={на первую игру выбирают один новый мяч, и один игранный}.
Н3={на первую игру выбирают два игранных мяча}.
Вероятности гипотез соответственно равны:
 ,
,  ,
, 
Проверка:  - выполняется:
- выполняется:  .
.
Пусть, событие А = {вторая игра проводится двумя новыми мячами}. Тогда условные вероятности следующие:
 ,
,  ,
, 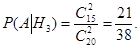
Вероятность события А найдем по формуле полной вероятности:
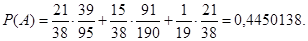
Пример . а) На грядке высажено 8 луковиц определенного сорта тюльпанов. Всхожесть луковиц 80%. Какова вероятность, что взойдет не менее 5, но не более 7 растений.
Решение. Событие А = {взойдет отдельный тюльпан}.
Событие В = {взойдет от 5 до 7 растений}.
Пусть событие В5={взойдет ровно 5 тюльпанов}, событие В6= {взойдет ровно 6 тюльпанов}, событие В7 ={взойдет ровно 7 тюльпанов}.
Вероятность события  , состоящего в том, что событие А произойдет ровно k раз при n независимых испытаниях, рассчитывается по формуле Бернулли:
, состоящего в том, что событие А произойдет ровно k раз при n независимых испытаниях, рассчитывается по формуле Бернулли:

 , где
, где  .
.
В частности,
 ,
,
 ,
,
 .
.
В данном случае имеем  . По теореме сложения для несовместных событий получаем
. По теореме сложения для несовместных событий получаем
Пример . Составить закон распределения дискретной случайной величины (ДСВ) Х - оценки, полученной на экзамене наугад выбранным студентом. Известно, что в группе из 20 человек 2 студента получили оценку – «2», 6 студентов – «3», 10 студентов – «4» и 2 студента – «5». Построить график функции распределения. Вычислить числовые характеристики 
Решение: ДСВ Х - отметка студента, которая может принять значения 2; 3; 4 или 5. Вероятность события { X =2} равна P ( X =2)= p 1 =2/20, (число двоек - 2, а общее число студентов 20). Вероятности других возможных значений равны:
 ,
,  ,
,  .
.
Следовательно, закон распределения ДСВ имеет вид:

| 2 | 3 | 4 | 5 |

| 0,1 | 0,3 | 0,5 | 0,1 |
Контроль: 0,1+0,3+0,5+0,1=1
Найдем числовые характеристики данной случайной величины. Математическое ожидание:
 .
.
Дисперсия:

Среднее квадратическое отклонение:

Функция распределения  имеет вид:
имеет вид:


График функции распределения имеет вид:

Пример . Из группы населения случайным образом отобрано 10 человек и собраны их доходы за истекший год в тысячах рублей х1, х2, х3…х10. Найти выборочное среднее исправленную выборочную дисперсию. Считая распределение доходов в группе нормальным и, применяя в качестве его параметров выборочные характеристики, определить, какой процент населения имеет годовой доход, превышающий 100 тыс. рублей.
| х1 | х2 | х3 | х4 | х5 | х6 | х7 | х8 | х9 | х10 |
| 80 | 110 | 130 | 100 | 70 | 90 | 150 | 60 | 90 | 70 |
Решение.
Найдем выборочную среднюю:
 .
.
Вычислим выборочную дисперсию  .
.
 , n =10.
, n =10.

Исправленная выборочная дисперсия:
 .
.
 .
.
Чтобы найти процент группы населения, которая имеет доход, превышающий 100 тыс. руб. используем формулу попадания значений нормально распределенной случайной величины в заданный промежуток:
 , где
, где  – функция Лапласа.
– функция Лапласа. 
В данном случае принимаем следующие значения параметров:
 = 100 тыс.руб.,
= 100 тыс.руб.,  тыс.руб.,
тыс.руб.,  тыс. руб.,
тыс. руб.,  тыс.руб. (нет ограничений сверху). Имеем:
тыс.руб. (нет ограничений сверху). Имеем: 
По таблице находим:  , следовательно,
, следовательно,  .
.
ОБРАЗЦЫ РЕШЕНИЯ ЗАДАЧ КОНТРОЛЬНОЙ РАБОТЫ №1
Пример 1. Даны матрицы  и
и  .
.  - единичная матрица. Найти:
- единичная матрица. Найти:
а) матрицу 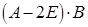 ; б) обратную матрицу
; б) обратную матрицу  и проверить, что
и проверить, что  :
:
 .
.
Решение. а). Раскроем скобки, получим
 .
.
Применяя правило умножения матрицы на матрицу, имеем
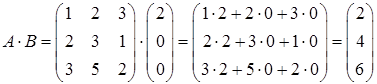 .
.
Следовательно,
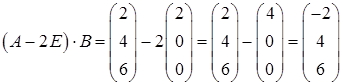 .
.
б). Обратную матрицу  найдем, используя присоединенную матрицу
найдем, используя присоединенную матрицу  . Элементы присоединенной матрицы - это алгебраические дополнения соответствующих элементов матрицы
. Элементы присоединенной матрицы - это алгебраические дополнения соответствующих элементов матрицы  , расположенные по столбцам:
, расположенные по столбцам:
 .
.
Обратная матрица определяется формулой:
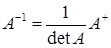 .
.
Вычислим определитель матрицы, проверим, что матрица невырожденная, следовательно, имеет обратную матрицу. Определитель найдем, раскрывая по элементам первой строки:
 .
.
Находим алгебраические дополнения элементов исходной матрицы  :
:



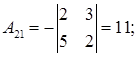




 .
.
Итак, присоединенная матрица имеет вид:
 .
.
Таким образом, обратная матрица равна
 .
.
Проверим, что обратная матрица найдена правильно, должно выполняться условие  . Вычислим элементы произведения матриц:
. Вычислим элементы произведения матриц:
 - верно,
- верно,
 - верно,
- верно,
 - верно.
- верно.
Пример 2. Тремя методами (Крамера, матричным методом и методом Гаусса) решить систему линейных алгебраических уравнений:  , где матрицы
, где матрицы  и
и  заданы в условии задачи 1, а
заданы в условии задачи 1, а  - матрица-столбец неизвестных
- матрица-столбец неизвестных 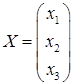 .
.
Решение. Учитывая правило перемножения матриц, запишем подробный вид системы:
 .
.
Получим решение по формулам Крамера:  . Здесь
. Здесь  - определитель матрицы системы, он найден в задаче 1 при нахождении обратной матрицы.
- определитель матрицы системы, он найден в задаче 1 при нахождении обратной матрицы.  - определители, полученные из определителя матрицы системы заменой соответственно первого, второго, третьего столбца матрицы столбцом правых частей:
- определители, полученные из определителя матрицы системы заменой соответственно первого, второго, третьего столбца матрицы столбцом правых частей:
 .
.
Таким образом, получаем,
 .
.
Получим решение матричным методом. В этом случае решение определяется формулой:
 .
.
Обратная матрица была найдена при решении задачи 1. Поэтому сразу запишем
 .
.
Сравнивая соответствующие элементы матриц слева и справа, снова находим
 .
.
Получим решение методом Гаусса. При помощи элементарных преобразований строк расширенной матрицы  последовательно исключаем неизвестные в уравнениях системы. На месте клетки
последовательно исключаем неизвестные в уравнениях системы. На месте клетки  получим единичную матрицу
получим единичную матрицу 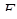 , при этом на месте клетки
, при этом на месте клетки  появится вектор решения.
появится вектор решения.


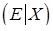 . Итак,
. Итак,  .
.
Пример 3. Даны точки
 . Найти:
. Найти:
а). Координаты, модуль и направляющие косинусы вектора  ;
;
б). Проекцию вектора  на вектор
на вектор  ;
;
в).Скалярное произведение векторов  и
и  , а также угол между ними;
, а также угол между ними;
г).Векторное произведение векторов  и
и  , а также площадь треугольника
, а также площадь треугольника  ;
;
д). Смешанное произведение векторов  , а также объем пирамиды ABCD.
, а также объем пирамиды ABCD.
Решение. а) Вектор  найдем по формуле
найдем по формуле  :
:  . Модуль вектора
. Модуль вектора  определяется соотношением
определяется соотношением  . Получаем отсюда
. Получаем отсюда 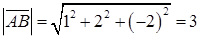 . Направляющие косинусы – это координаты орта вектора
. Направляющие косинусы – это координаты орта вектора  . Т.е. вектора
. Т.е. вектора  . Направляющие косинусы равны:
. Направляющие косинусы равны:  .
.
б). Проекцию вектора вычислим с помощью скалярного произведения:
 .
.
Найдем вектор  . Учитывая формулу вычисления скалярного произведения векторов в координатах
. Учитывая формулу вычисления скалярного произведения векторов в координатах
 ,
,
найдем проекцию
 .
.
в). Найдем вектор  и вычислим скалярное произведение векторов
и вычислим скалярное произведение векторов 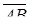 и
и  .
.  .
.  .
.
Косинус угла  между векторами
между векторами  и
и  определяется равенством
определяется равенством
 .
.
Отсюда заключаем, что угол  .
.
Найдем вектор  и вычислим векторное произведение векторов с помощью формулы
и вычислим векторное произведение векторов с помощью формулы
 .
.
 .
.  . Учитывая, что модуль векторного произведения – площадь параллелограмма, для площади треугольника имеем соотношение
. Учитывая, что модуль векторного произведения – площадь параллелограмма, для площади треугольника имеем соотношение
 .
.
д). Найдем вектор  и вычислим смешанное произведение по формуле
и вычислим смешанное произведение по формуле
 .
.
Имеем  .
.  .
.
Учитывая, что модуль смешанного произведения численно равен объему параллелепипеда, построенного па векторах-сомножителях, а объем пирамиды составляет шестую часть объема параллелепипеда, получаем
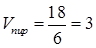 .
.
Пример 4. . На плоскости даны вершины треугольника  . Найти:
. Найти:
а). Канонические уравнения сторон  и
и  ;
;
б). Уравнение высоты, опущенной из вершины B;
в). Внутренний угол 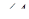 ;
;
г). Уравнение медианы, проведенной из вершины B;
д). Расстояние от точки В до стороны  . Сделать чертеж:
. Сделать чертеж:
 .
.
Решение. а). Уравнения сторон найдем, используя уравнение прямой, проходящей через две заданные точки:  .
.

 Угловой коэффициент прямой
Угловой коэффициент прямой  равен
равен  .
.
б). Угловой коэффициент высоты  связан с угловым коэффициентом стороны
связан с угловым коэффициентом стороны  соотношением
соотношением  . Отсюда находим,
. Отсюда находим,  . Уравнение высоты составим, используя уравнение прямой, имеющей заданный наклон и проходящей через заданную точку:
. Уравнение высоты составим, используя уравнение прямой, имеющей заданный наклон и проходящей через заданную точку: 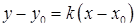 .
.
 .
.
в). Для нахождения внутреннего угла  используем формулу
используем формулу
 .
.
Получаем,  .
.  .
.
г). Чтобы составить уравнение медианы, найдем координаты точки  - середины стороны
- середины стороны  :
:  .
.
 (каноническое уравнение вертикальной прямой).
(каноническое уравнение вертикальной прямой).
д). Расстояние от вершины  до стороны
до стороны  найдем по формуле:
найдем по формуле:
 , где
, где  - общее уравнение прямой,
- общее уравнение прямой,  -
-
точка, от которой определяется расстояние. Общее уравнение стороны  имеет вид:
имеет вид:  . Поэтому
. Поэтому  .
.
Строим треугольник в координатных осях:

Пример 5. Точки  являются вершинами пирамиды. Найти:
являются вершинами пирамиды. Найти:
а). Уравнения ребра  ;
;
б). Угол между ребрами  и
и  ;
;
в). Уравнение грани  ;
;
г). Угол между ребром  и гранью
и гранью  ;
;
д). Уравнение высоты пирамиды, опущенной из вершины  , а также проекцию этой вершины на плоскость
, а также проекцию этой вершины на плоскость  .
.
Решение. а). Канонические уравнения прямой в пространстве, проходящей через две заданные точки, определяются соотношениями
 .
.
Следовательно, уравнения ребра  имеют вид
имеют вид
 , или
, или  .
.
б). Угол между ребрами - это угол  между векторами
между векторами  и
и  .
.
Эти векторы соответственно равны  и
и  . Поэтому
. Поэтому
 .
.
в). Составим уравнение грани  , используя условие компланарности векторов
, используя условие компланарности векторов  ,
,  и текущего вектора
и текущего вектора  :
:
 .
.
Раскрывая определитель, получим
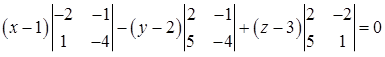 , или
, или
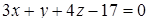 .
.
г). Угол 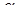 между прямой с направляющим вектором
между прямой с направляющим вектором  и плоскостью с нормальным вектором
и плоскостью с нормальным вектором  определяется формулой
определяется формулой
 .
.
Направляющий вектор ребра равен  , координаты нормального вектора плоскости – это коэффициенты в общем уравнении плоскости, т.е.
, координаты нормального вектора плоскости – это коэффициенты в общем уравнении плоскости, т.е.  . Отсюда получаем
. Отсюда получаем
 ,
,  .
.
д). Направляющим вектором высоты пирамиды, опущенной из вершины  , является нормальный вектор плоскости
, является нормальный вектор плоскости  . Поэтому канонические уравнения высоты следующие
. Поэтому канонические уравнения высоты следующие
 .
.
Проекцию  вершины
вершины  на плоскость основания найдем как пересечение прямой
на плоскость основания найдем как пересечение прямой 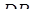 и плоскости
и плоскости  . Для этого от канонических уравнений высоты перейдем к параметрическим уравнениям:
. Для этого от канонических уравнений высоты перейдем к параметрическим уравнениям:

Подставляя последние соотношения в уравнение плоскости  , получаем уравнение для определения значения параметра
, получаем уравнение для определения значения параметра  , соответствующего точке
, соответствующего точке  :
:
 .
.
Подставляя полученное значение  в параметрические уравнения высоты, находим координаты точки
в параметрические уравнения высоты, находим координаты точки  :
:
 .
.
Пример 6. Найти пределы функций: а)  ; б)
; б)  ;
;
в) 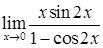 ; г)
; г) 
Решение.
а)  Чтобы раскрыть неопределенность типа
Чтобы раскрыть неопределенность типа  необходимо и в числителе и в знаменателе в каждом из сомножителей вынести старшие степени =
необходимо и в числителе и в знаменателе в каждом из сомножителей вынести старшие степени =  ;
;
б) 
в)  ;
;
Здесь использован первый замечательный предел:  .
.
г) 
Здесь применен второй замечательный предел:  .
.
Пример 7. Используя определение, найти производную функции  в точке
в точке  .
.
Решение.
По определению  .
.

Отсюда  .
.
Для решения примеров задания 8 предполагается использование правил дифференцирования и таблицы производных основных элементарных функций:
|
из
5.00
|
Обсуждение в статье: ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

