Правила записи ФАЛ в СДНФ и СКНФ

В СДНФ функция f(х_n,…,х₁) представляется в виде дизъюнкции функций, которые называются конституентами единицы. Конституента единицы имеет также другие названия: характеристическая функция единицы, минтерм.

Конституента единицы – это ФАЛ n переменных, которая равна единице только на одном наборе переменных. На остальных наборах конституента единицы равна нулю.

Число различных конституент единицы среди функций n переменных равно 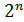, т.е. числу различных наборов n переменных. Конституенту единицы будем обозначать буквой m с индексом, равным номеру набора, на котором конституента единицы равна единице. Обычно конституенты единицы выражают в виде конъюнкции всех переменных, каждая из которых входит в конъюнкцию один раз в прямой или инверсной форме.

Конституенту единицы m_i в виде конъюнкции n переменных получают следующим образом: записывают конъюнкцию n переменных, располагая последние в определенной последовательности, например, начиная с переменной с наибольшим номером, и двоичное n-разрядное число, равное i; над переменными, позиции которых совпадают с позициями нулей в двоичном числе i, ставят знаки отрицания.

Пример 1. Записать конституенту единицы m₂₇, n=6.

Записываем 6-разрядное двоичное число, равное 27: 27_{10) = 011011₍₂₎ и конъюнкцию шести переменных, начиная со старшей переменной х₆: x₆x₅x₄x₃x₂x₁. Из записи двоичного числа 011011 следует, что знаки отрицания нужно поставить над шестой и третьей переменными: m₂₇ = ₆х₅х_{4 3}х₂х₁.

Дизъюнкция конституент единицы, равных единице на тех же наборах, что и заданная функция, называется СДНФ ФАЛ.

Любая ФАЛ f(x_n,…,x₁), кроме константы нуль, может быть представлена в СДНФ:

f(x_n,…,x₁) = m_j1Úm_j2Ú…Úm_jl, (1)

где j1, j2,…, jl– номера наборов, на которых ФАЛ равна единице; l– число таких наборов, на которых ФАЛ равна единице.

Справедливость соотношения (1) вытекает из того, что каждая единица функции f(x_n,…,x₁) в ее СДНФ представляется конституентой единицы с соответствующим номером. Из соотношения (1) следует, что любая ФАЛ имеет единственную СДНФ.

Структура СДНФ такова, что на произвольном наборе переменных в правой части соотношения (1) или все конституенты единицы равны нулю, если функция на этом наборе равна нулю, или только одна из конституент единицы равна единице, а остальные равны нулю, если функция на этом наборе равна единице. Поэтому справедливость соотношения (1) сохранится, если в нем знак дизъюнкции заменить на знак сложения по модулю два:

f(x_n,…,x₁) = m_j1 Åm_j2Å…Åm_jl. (2)

Представление ФАЛ в виде (2) называют совершенной полиномиальной нормальной формой (СПНФ).

Любая ФАЛ может быть задана таблицей ее значений в зависимости от значений переменных. Переход от табличного представления ФАЛ к алгебраическому в виде СДНФ выполняют в такой последовательности:

-записывают ряд конъюнкций всех переменных и соединяют их знаками дизъюнкции; количество конъюнкций равно числу наборов, на которых заданная ФАЛ равна единице;

-под каждой конъюнкцией записывают набор переменных, на котором ФАЛ равна единице; над переменными, равными нулю в этом наборе, ставят знаки отрицания.

Это правило называют правилом записи ФАЛ по единицам, т.е. по единичным значениям функции.

Пример 2. Представить функцию φ(x₃, x₂, x₁), заданную табл. 1, в СДНФ.

Так как функция φ(x₃, x₂, x₁) трех переменных принимает значение, равное единице, на четырех наборах переменных, то записываем четыре конъюнкции трех переменных, объединенные знаком дизъюнкции, и под каждой конъюнкцией – соответствующие наборы переменных:

x₃x₂x₁ Úx₃x₂x₁ Úx₃x₂x₁Úx₃x₂x₁

0 1 0 1 0 0 1 0 1 1 1 1.

Расставляя знаки отрицания над переменными, равными нулю в каждом наборе, получим:

Пример 3. Представить функцию штрих Шеффера f₁₄(x₂, x₁) в СДНФ.

Функция f₁₄(x₂, x₁) равна единице на трех наборах переменных: 0,0; 0,1 и 1,0. Поэтому .Эту форму функции f₁₄(x₂, x₁) можно преобразовать и привести к принятой записи:

В СКНФ заданная ФАЛ f(x_n, …, x₁) представляется в виде конъюнкции функций, которые называются конституентами нуля. Конституента нуля имеет также другие названия: характеристическая функция нуля, макстерм.

Конституента нуля – это ФАЛ n переменных, которая равна нулю только на одном наборе переменных. Число различных конституент нуля равно 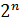, т.е. числу различных наборов переменных. Конституенты нуля будем обозначать буквой М с индексом, равным номеру набора, на котором конституента нуля равна нулю. Обычно конституенты нуля выражают в виде дизъюнкции всех переменных, каждая из которых входит в дизъюнкцию в прямой или инверсной форме.

Конституенту нуля М_i в виде дизъюнкции n переменных получают следующим образом:

-записывают дизъюнкцию n переменных и двоичное n-разрядное число, равное i;

-над переменными, позиции которых совпадают с позициями единиц в двоичном числе i, ставят знаки отрицания.

Пример 4. Записать конституенту нуля М₂₇, n=6.

Запишем дизъюнкцию шести переменных, начиная с первого: x₆Úx₅Úx₄Úx₃Úx₂Úx₁ и 6-разрядное двоичное число, равное 27: 27₍₁₀₎ = 011011₍₂₎. Расставляя знаки отрицания над первой, второй, четвертой и пятой переменными, получим конституенту нуля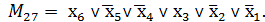

Конъюнкция конституент нуля, равных нулю на тех же наборах, что и заданная функция, называется СКНФ ФАЛ.

Любая ФАЛ, кроме константы единицы, может быть представлена в СКНФ

f(x_n,…,x₁) = M_j1×M_j2×… ×M_jl, (3)

где j1, j2, …, jl – номера наборов, на которых функция равна нулю; l – число таких наборов.

Справедливость соотношения (3) следует из того, что каждый нуль функции f(x_n,…,x₁) в ее СКНФ представляется конституентой нуля с соответствующим номером, которая обращает функцию на данном наборе в нуль. Из соотношения (3) следует, что любая ФАЛ имеет единственную СКНФ.

Структура СКНФ такова, что на произвольном наборе переменных в правой части соотношения (3) или только одна конституента нуля равна нулю, а остальные равны единице, если функция на этом наборе равна нулю; или все конституенты нуля равны единице, если функция на этом наборе равна единице. Так как на любом наборе переменных одновременное равенство нулю двух и более конституент нуля исключено, то справедливость соотношения (3) сохранится, если в нем знак конъюнкции заменить на знак эквивалентности:

f(x_n, …, x₁) = M_j1ºM_j2ºMº…ºM_jl. (4)

Совершенная форма в виде (4) не имеет установившегося названия. Переход от табличного представления ФАЛ к алгебраическому в виде СКНФ выполняют в такой последовательности:

-записывают ряд дизъюнкций всех переменных и объединяют их знаком конъюнкции; количество дизъюнкций равно числу наборов, на которых заданная ФАЛ равна нулю;

-под каждой дизъюнкцией записывают набор переменных, на котором функция равна нулю;

-над переменными, которые в данном наборе равны единице, ставят знаки отрицания

Так как функция f(x₃, x₂, x₁) равна нулю на пяти наборах переменных (табл. 1), то записываем пять дизъюнкций трех переменных и объединяем их знаком конъюнкции; под дизъюнкциями записываем наборы, на которых функция равна нулю:

(x₃Úx₂Úx₁)(x₃Úx₂Úx₁)( x₃Úx₂Úx₁)( x₃Úx₂Úx₁)( x₃Úx₂Úx₁)

0 0 0 0 1 0 1 0 0 1 1 0 1 1 1.

Поставив знаки отрицания над переменными, равными единице, получим:

f(x₃, x₂, x₁) = (x₃ ˅ x₂ ˅ x₁)( x₃ ˅

Пример 5. Представить функцию стрелка Пирса f₈(x₂, x₁) в СКНФ.

Функция f₈(x₂,x₁) равна нулю на трех наборах переменных: 0,1; 1,0 и 1,1. Поэтому

СКНФ функции f₈(x₂,x₁) можно преобразовать к виду:

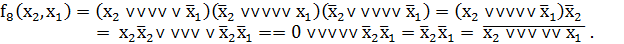
Отметим, что по определению , т.е. конституенты нуля и единицы, имеющие одинаковые индексы, инверсны друг другу. Например, Действительно, так как, М₁₁ =

= ₁₁ = , то, согласно правилу де Моргана, справедливо равенство СДНФ называют формой И/ИЛИ, что говорит о том, что в данной форме внутренней операцией является конъюнкция (И), а внешней – дизъюнкция (ИЛИ). СКНФ называют формой ИЛИ/И, в которой внутренняя операция – дизъюнкция, а внешняя - конъюнкция. Внутренняя операция выполняется первой, а внешняя – последней.

Наиболее широкое распространение получили базисы ФАЛ И-НЕ и ИЛИ-НЕ. Логические элементы И-НЕ и ИЛИ-НЕ являются базовыми (основными) в сериях интегральных схем (ИС) ДТЛ, ТТЛ, ТТЛШ, ЭСЛ, КМОП-логики. Поэтому после нахождения минимальных ДНФ и КНФ часто возникает необходимость представления этих форм в базисах функций И-НЕ и ИЛИ-НЕ.