 |
Главная |
Метод Квайна минимизации ФАЛ
|
из
5.00
|
При минимизации по методу Квайна заданную ФАЛ f(хn,…, х1) нужно представить в СДНФ, если она не задана в этой форме.
Если ФАЛ задана в произвольной ДНФ, то элементарные конъюнкции с помощью операции развертывания нужно представить в виде конституент единицы. Операция развертывания заключается в умножении элементарных конъюнкций, не являющихся конституентами единицы, на выражение типа (  , где хi – переменная, отсутствующая в записи элементарной конъюнкции.
, где хi – переменная, отсутствующая в записи элементарной конъюнкции.
Если ФАЛ задана в произвольной форме, то эту функцию всегда можно привести к табличной форме, а от нее перейти к СДНФ.
Этапы минимизации ФАЛ по методу Квайна:
1. Нахождение сокращенной ДНФ. Для этого выполняются операции неполного склеивания и поглощения с целью поиска всех простых импликант функции. Сначала попарно сравниваются все конституенты единицы СДНФ функции. Если какие-либо две конституенты единицы отличаются друг от друга только одной переменной (в одной хi, а в другой  , то выписывают их общую часть, а против этих конституент единицы ставят метки. Замена двух конституент единицы вида Aхi и A
, то выписывают их общую часть, а против этих конституент единицы ставят метки. Замена двух конституент единицы вида Aхi и A  является результатом их склеивания по аргументу хi: Aхi ∨ A
является результатом их склеивания по аргументу хi: Aхi ∨ A  .
.
Метки означают, что отмеченные ими конституенты единицы поглощаются импликантой А. Таким образом получаются все импликанты, являющиеся конъюнкциями (n-1)-го ранга. Полученные элементарные конъюнкции (n-1)-го вновь сравнивают попарно, находят импликанты, являющиеся конъюнкциями (n-2)-го ранга, склеивающиеся конъюнкции (n-2)-го отмечают метками и т.д. Этап заканчивается, когда вновь полученные конъюнкции r-го ранга уже не склеиваются между собой. Все неотмеченные конъюнкции являются простыми импликантами. Неотмеченными могут оказаться и исходные конституенты единицы. Дизъюнкция всех простых импликант и есть сокращенная ДНФ заданной ФАЛ.
2. Нахождение существенных импликант. Задача данного этапа - определить простые импликанты, которые должны обязательно входить в минимальную ДНФ, т.е. существенные импликанты. На последующих этапах определяются простые импликанты, которые можно не включать в минимальную ДНФ.
Для поиска существенных импликант составляется таблица с числом строк, равным числу простых импликант, и числом столбцов, равным числу конституент единицы минимизируемой функции. Строки обозначают простыми импликантами, а столбцы – конституентами единицы функции. На пересечении строки с импликантой и столбца с конституентой единицы, поглощаемой этой импликантой, ставят метки.
Если в каком-либо столбце таблицы имеется только одна метка, то простая импликанта, стоящая в строке с этой меткой, является существенной импликантой. Существенная импликанта должна обязательно входить в минимальную ДНФ, так как она является единственной простой импликантой, которая поглощает данную конституенту единицы. Поэтому из таблицы исключаются строки, соответствующие существенным импликантам, и столбцы конституент единицы, поглощаемых этими существенными импликантами.
3. Исключение лишних столбцов и строк. Анализируется таблица, полученная после выполнения второго этапа. Если в ней имеются два столбца, содержащие метки в одних и тех же строках, то один из столбцов можно исключить. Это возможно потому, что одна из импликант, которая поглощает конституенты единицы оставшегося и исключенного столбцов, будет включена в минимальную ДНФ функции.
Если после исключения некоторых столбцов в таблице появятся строки, не содержащие меток, то простые импликанты, соответствующие этим строкам, исключаются из дальнейшего рассмотрения, так как они не поглощают оставшиеся конституенты единицы.
4. Выбор минимальной ДНФ. Анализируя таблицу, полученную после выполнения третьего этапа, выбирают совокупность простыхимпликант, которые перекрывают своими метками все столбцы таблицы. Возможны несколько вариантов такого выбора. Дизъюнкция простыхимпликант этой совокупности и существенных импликант, полученных при выполнении второго этапа, является тупиковой ДНФ минимизируемой функции. Число различных тупиковых форм равно числу выбранных совокупностей простых импликант, полученных при выполнении этого этапа. Из тупиковых форм выбирают минимальную ДНФ функции, т.е. тупиковую форму, имеющую минимальное число букв. Минимальных форм может быть несколько.
Пример 6. Найти минимальную ДНФ функции
f(х4,х3,х2,х1)=  ∨
∨  ∨
∨ 
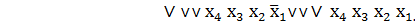
Так как функция задана в виде произвольной ДНФ, то приведем ее к СДНФ, умножив первую конъюнкцию функции на ( 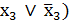 , вторую – на (
, вторую – на (  Тогда получим:
Тогда получим:
f(х4,х3,х2,х1)=  ∨
∨ 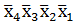 ∨
∨  ∨
∨

Решение.
1. Найдем простые импликанты.
Конституенты единицы (элементарные конъюнкции 4-го ранга):
1)  *, 2)
*, 2)  *, 3)
*, 3)  *, 4)
*, 4)  *,
*,
5)  6)
6)  *, 7)
*, 7)  *, 8)
*, 8) 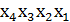 *.
*.
Сравнивая первую конституенту единицы списка с последующими, затем вторую с последующими и т.д.,находим пары конституент единицы, которые отличается только одной переменной. Такие конъюнкции склеиваются по этой переменной. После выполнения всех сравнений получим элементарные конъюнкции 3-го ранга:
1)  *, 2)
*, 2)  *, 3)
*, 3)  , 4)
, 4) 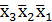 *,
*,
5)  , 6)
, 6)  *, 7)
*, 7)  , 8)
, 8)  .
.
Сравнивая элементарные конъюнкции 3-го ранга, а, именно, первую с последующими, вторую с последующими и т.д., получим элементарную конъюнкцию 2-го ранга  На этом процесс сравнения закончен. Простыми импликантами являются конъюнкции, не отмеченные знаком «*»:
На этом процесс сравнения закончен. Простыми импликантами являются конъюнкции, не отмеченные знаком «*»:  Знак «*» означает, что конъюнкции, отмеченные этим знаком, поглощаются другими конъюнкциями, не отмеченные этим знаком. Дизъюнкция всех простых импликант – это сокращенная ДНФ.
Знак «*» означает, что конъюнкции, отмеченные этим знаком, поглощаются другими конъюнкциями, не отмеченные этим знаком. Дизъюнкция всех простых импликант – это сокращенная ДНФ.
2. Найдем существенные импликанты функции, для чего составим импикантную таблицу. ФАЛ содержит восемь конституент единицы и имеет пять импликант. Поэтому импликантная таблица содержит восемь столбцов и пять строк с метками, определяющими вхождение конституент единицы в соответствующие импликанты функции (табл. 2).
Таблица 2
| Конст. ед. Пр. импл. | 
| 
| 
| 
| 
| 
| 
| 
| |

| * | * | |||||||

| * | * | |||||||

| * | * | |||||||

| * | * | |||||||

| * | * | * | * | |||||
Существенными импликантами являются конъюнкции  Поэтому из табл. 2 исключаем строки, соответствующие этим импликантам, и столбцы 2, 3, 4, 5, 6, 7 конституент единицы, поглощаемых этими импликантами. Тогда получим табл. 3.
Поэтому из табл. 2 исключаем строки, соответствующие этим импликантам, и столбцы 2, 3, 4, 5, 6, 7 конституент единицы, поглощаемых этими импликантами. Тогда получим табл. 3.
Таблица 3
| Конституента единицы Простая импликанта |

| 
|



| * * | * * |
3. Лишних столбцов и строк в ней нет. Оставшиеся в табл.3 конституенты единицы могут быть представлены в тупиковых ДНФ импликантой  или дизъюнкцией импликант
или дизъюнкцией импликант  ∨
∨ 
4. Тупиковыми ДНФ являются:
fтуп1(х4, х3, х2, х1) =  ∨
∨  ∨
∨ 
fтуп2(х4, х3, х2, х1) =  ∨
∨  ∨
∨  ∨
∨  .
.
Минимальной формой данной ФАЛ является
fмин(х4, х3, х2, х1) =  ∨
∨  ∨
∨ 
Последний этап может быть и простым, и очень сложным. Поэтому для выполнения этого этапа в случае сложности выбора всех совокупностей простых импликант можно рекомендовать метод Петрика, позволяющий аналитически найти все тупиковые и все минимальные ДНФ.
При большом числе переменных трудоемкость метода Квайна возрастает, что связано с необходимостью полного попарного сравнения всех конъюнкций при нахождении простых импликант. Метод Квайна-Мак-Класки упрощает поиск простых импликант за счет уменьшения числа сравнений. Однако более эффективным при числе переменных 4-6 является применение карт Карно для нахождения простых и существенных импликант. Таким образом упрощается выполнение первого и второго этапов метода Квайна.
Метод Квайна с применением карт Карно и преобразования Петрика позволяет найти все тупиковые и все минимальные формы ФАЛ аналитически, исключив этап выбора простых импликант для покрытия всех столбцов импликантной таблицы ФАЛ.
Карты Карно.
Карта Карно является таблицей для графического способа представления ФАЛ. Карта Карно функции n переменных представляет собой матрицу из 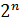 клеток и обычно имеет квадратную или прямоугольную форму, близкую к квадратной. Переменные ФАЛ разбиваются на две равные или отличающиеся на единицу группы (в зависимости от четного или нечетного их числа). Одна группа переменных служит для нумерации столбцов, другая – для нумерации строк карты Карно. Столбцы и строки таблицы отмечаются номерами наборов переменных, порядок следования номеров наборов соответствует двоичному коду Грея.
клеток и обычно имеет квадратную или прямоугольную форму, близкую к квадратной. Переменные ФАЛ разбиваются на две равные или отличающиеся на единицу группы (в зависимости от четного или нечетного их числа). Одна группа переменных служит для нумерации столбцов, другая – для нумерации строк карты Карно. Столбцы и строки таблицы отмечаются номерами наборов переменных, порядок следования номеров наборов соответствует двоичному коду Грея.
Код Грея относится к группе кодов, носящих название отраженных (рефлексных – от английского слова toreflect – отражать) кодов. Отличительной особенностью этих кодов является то, что соседние кодовые комбинации различаются цифрой только в одном разряде. Код Грея получил большее распространение из всего множества отраженных кодов, так как достаточно просто преобразуется в простой двоичный код.
Характерные особенности кода Грея:
1. Каждая комбинация отличается от соседних только в одной позиции (в одном разряде).
2. Смена значений элементов в каждом разряде при переходах от комбинации к комбинации происходит в два раза реже, чем в простом двоичном коде.
3. В коде Грея можно выделить оси симметрии (оси отражения). Относительно осей симметрии имеет место ʺзеркальноеʺ расположение (отражение) символов в некоторых разрядах. Так, в двухразрядном коде (см. первые два столбца справа и первые четыре строки табл.4) имеет место ʺзеркальноеʺ расположение символов в первом разряде относительно оси, проведенной между строками 1 – 2; в трехразрядном коде (см. первые три столбца справа и восемь строк табл.4) имеет место ʺзеркальноеʺ расположение символов в двух младших разрядах относительно оси, проведенной между строками 3 – 4, а также в младшем разряде относительно осей 1 – 2 и 5 – 6; в четырехразрядном коде имеет место ʺзеркальноеʺ расположение символов в трех младших разрядах относительно оси, проведенной между строками 7 – 8, в двух младших разрядах относительно осей 3 – 4 и 11 – 12, а также в младшем разряде относительно осей 1 – 2, 5 – 6, 9 – 10, 11 – 12. Ось симметрии, которая проходит в n-разрядном коде Грея между комбинациями, соответствующими числам  называется главной осью симметрии. Относительно нее симметрично (т.е.ʺзеркальноʺ) расположены символы в (n – 1) разрядах кода Грея. Для четырехразрядного кода Грея главная ось проходит между стоками 7 – 8, относительно которой ʺзеркальноʺ расположены символы в трех младших разрядах.
называется главной осью симметрии. Относительно нее симметрично (т.е.ʺзеркальноʺ) расположены символы в (n – 1) разрядах кода Грея. Для четырехразрядного кода Грея главная ось проходит между стоками 7 – 8, относительно которой ʺзеркальноʺ расположены символы в трех младших разрядах.
Правило перевода простого двоичного кода в код Грея:
1) под двоичным числом записывают такое же число со сдвигом вправо на один разряд, при этом младший разряд сдвигаемого числа отбрасывается;
2) поразрядно (т.е. без учета переносов) суммируют несдвинутое и сдвинутое двоичные числа по модулю два.
Результат суммирования дает изображение исходного двоичного числа в коде Грея.
В табл.4 приведены десятичные числа от 0 до 15, выраженные комбинациями простого двоичного кода и кода Грея.
Таблица 4
| Десятичное число | Простой двоичный код | Код Грея |
На рис. 1,а,б,в,г приведены карты Карно для функций двух, трех, четырех и пяти переменных соответственно.
Рис. 1. Карты Карно двух, трех, четырех и пяти переменных
Карты Карно для функций большего числа переменных строятся из карт для меньшего числа переменных. Например, карта Карно для трех переменных составлена из двух карт Карно для двух переменных, карта Карно для четырех переменных составлена из двух карт Карно для трех переменных или из четырех карт Карно для двух переменных.
На рис. 1 в качестве некоторых примеров короткими отрезками линий (оси симметрии, или оси «отражения») отмечены границы карт меньшего числа переменных, из которых строятся карты Карно большего числа переменных. Например, карта Карно для трех переменных (рис. 1,б) состоит из двух карт для двух переменных х2 и х1, столбцы которых соединены по границе, отмеченной вертикальным отрезком линии. Нумерация столбцов левой карты для двух переменных х2,х1 следует в порядке 0, 1, а для правой – 1, 0, т.е. идет отражение («зеркальное») порядка нумерации столбцов по переменной х2. Левая карта для двух переменных х2, х1 соответствует переменной  , правая – х3, а поэтому нумерация столбцов по переменным х3, х2 имеет порядок 00, 01, 11, 10. Аналогично можно представить, что карта Карно для пяти переменных составлена из двух карт для четырех переменных. Левая карта для четырех переменных имеет порядок нумерации столбцов по переменным х4, х3 00, 01, 11, 10, правая –10, 11, 01, 00, т.е. отраженный («зеркальный»). Левая карта Карно четырех переменных х4, х3, х2 х1 соответствует переменной
, правая – х3, а поэтому нумерация столбцов по переменным х3, х2 имеет порядок 00, 01, 11, 10. Аналогично можно представить, что карта Карно для пяти переменных составлена из двух карт для четырех переменных. Левая карта для четырех переменных имеет порядок нумерации столбцов по переменным х4, х3 00, 01, 11, 10, правая –10, 11, 01, 00, т.е. отраженный («зеркальный»). Левая карта Карно четырех переменных х4, х3, х2 х1 соответствует переменной  , правая – переменной х5. Поэтому нумерация столбцов по переменным х5, х4, х3 карты Карно для пяти переменных имеет порядок 000, 001, 011, 010, 110, 111, 101, 100. Далее на картах Карно разделение на карты меньшего числа переменных отрезками линий не отмечается, но подразумевается.
, правая – переменной х5. Поэтому нумерация столбцов по переменным х5, х4, х3 карты Карно для пяти переменных имеет порядок 000, 001, 011, 010, 110, 111, 101, 100. Далее на картах Карно разделение на карты меньшего числа переменных отрезками линий не отмечается, но подразумевается.
Каждой клетке на карте Карно соответствует определенный набор переменных. Например, на карте Карно для пяти переменных клетке, расположенной на пересечении столбца 010 и строки 11, соответствует набор 0, 1, 0, 1, 1 переменных х5, х4, х3, х2, х1.
Карта заполняется в соответствии с таблицей истинности: значения 1 записываются в клетках, соответствующих наборам, на которых функция равна 1. Значения 0 функции в клетках карты обычно опускаются и эти клетки остаются пустыми. Применяется и другой способ нанесения функции на карту Карно нулями в те ячейки, на наборах которых функция равна нулю. Клетки, соответствующие наборам, на которых функция равна 1, остаются пустыми.
Одно из преимуществ карт Карно состоит в том, что на нее можно наносить функцию, заданную в произвольной ДНФ.
Важным достоинством карт Карно является то, что с их помощью быстро находятся простые и существенные импликанты функции. Если карту Карно свернуть в цилиндр относительно горизонтальной или вертикальной оси, то клетки, расположенные в противоположных концах одной строки или одного столбца карты, окажутся соседними. Соседними в этом случае являются и карты для меньшего числа переменных, из которых составлена карта Карно заданного числа переменных. Поэтому про такие клетки или карты будем также говорить, что они являются соседними. Соседние конституенты единицы (нуля) функции располагаются на карте Карно в соседних клетках.
Две конституенты единицы (нуля) склеиваются, если:
-они расположены в соседних клетках одной строки или одного столбца;
-они расположены в противоположных клетках одной строки или одного столбца;
-они находятся в клетках, симметрично расположенных относительно осей симметрии карт для двух, трех, четырех и большего числа переменных, а сами карты расположены по соседству друг с другом или в противоположных концах столбцов или строк карт (не клеток).
Переменная, по которой происходит склеивание двух конституент единицы, это та переменная, которая меняет свое значение при переходе границы клеток этих конституент единицы или соседних карт Карно меньшего числа переменных, в которых они расположены.
На рис. 2 приведена карта Карно для шести переменных x6, x5,…, x1, составленная из восьми карт для трех переменных или из четырех карт для четырех переменных.
Рис. 2. Примеры склеивающихся конституент единицы
Поясним правила нахождения склеивающихся конституент единицы. Конституента единицы, обозначенная на карте Карно (рис. 2) буквой a(  склеивается с соседними конституентами единицы b(по переменной х1), с (по переменной х4), d (по переменной х3), расположенных в соседних клетках карты трех переменных, а также с конституентами единицы i (по переменной х5), h (по переменной х6), расположенных в соседних картах, а каждая из клеток i и h расположена симметрично с клеткой a относительно границ раздела карт для трех переменных. Kонституенты единицы a и e не склеиваются, так как расположены несимметрично относительно границы соседних карт Карно для трех переменных. Конституента единицы а не склеивается с конституентами единицы j и f, так как карты Карно трех переменных, в которых они расположены, не являются соседними с картой Карно трех переменных, в которой расположена конституента единицы а.
склеивается с соседними конституентами единицы b(по переменной х1), с (по переменной х4), d (по переменной х3), расположенных в соседних клетках карты трех переменных, а также с конституентами единицы i (по переменной х5), h (по переменной х6), расположенных в соседних картах, а каждая из клеток i и h расположена симметрично с клеткой a относительно границ раздела карт для трех переменных. Kонституенты единицы a и e не склеиваются, так как расположены несимметрично относительно границы соседних карт Карно для трех переменных. Конституента единицы а не склеивается с конституентами единицы j и f, так как карты Карно трех переменных, в которых они расположены, не являются соседними с картой Карно трех переменных, в которой расположена конституента единицы а.
По принципу соседства расположения клеток и карт можно определить группы  клеток, содержащих единицы и образующих квадрат или прямоугольник. Эти группы
клеток, содержащих единицы и образующих квадрат или прямоугольник. Эти группы  клеток с единицами склеиваются сразу по kпеременным.
клеток с единицами склеиваются сразу по kпеременным.
Конституенты единицы, образующие группу  соседних клеток, склеиваются по переменным, которые меняют свои значения при переходе через границы клеток группы и при переходе границы соседних карт меньшего числа аргументов, если группа располагается в нескольких соседних картах. На рис. 3 приведены примеры групп склеивающихся конституент единицы.
соседних клеток, склеиваются по переменным, которые меняют свои значения при переходе через границы клеток группы и при переходе границы соседних карт меньшего числа аргументов, если группа располагается в нескольких соседних картах. На рис. 3 приведены примеры групп склеивающихся конституент единицы.
Рис. 3. Примеры групп склеивающихся конституент единицы
Карты Карно позволяют легко и быстро находить простые и существенные импликанты функции по следующему алгоритму:
1. Выбирается клетка, содержащая «единицу», и определяются все возможные группы этой клетки с другими клетками, содержащими«единицы». Группам клеток, соответствуют конъюнкции, ранг которых меньше ранга конституент единицы. Определяют эти конъюнкции, соответствующие группам клеток, содержащих «единицы».
2. Анализируются эти группы. Если все «единицы» одной группы содержатся в другой группе, то первую вычеркивают. Невычеркнутые группы являются простыми импликантами.
Если для рассматриваемой клетки с «единицей» невычеркнутой осталась одна группа, то соответствующая ей конъюнкция является также и существенной импликантой. Если клетка с «единицей» ни с какой другой не склеивается, то соответствующая этой клетке конституента единицы является и простой, и существенной импликантой.
3. Повторяются пункты 1 и 2 для каждой клетки карты, содержащей «единицу», т.е. для каждой конституенты единицы. При достаточном опыте запись всех промежуточных групп становится ненужной, поэтому сразу записываются простыеимпликанты.
|
из
5.00
|
Обсуждение в статье: Метод Квайна минимизации ФАЛ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

