Уравнивание системы нивелирных ходов с одной узловой точки

Б3.Б.5 ГЕОДЕЗИЯ

Б3.Б.2 ГЕОДЕЗИЯ

Практическое занятие.

Уравнивание системы нивелирных и теодолитных ходов

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

 

Направление: 120700 Землеустройство и кадастры

120100 Геодезия и дистанционное зондирование

Степень: бакалавр

 

 

 

УДК 528

ББК 26.11

М 54

 

 

Рекомендовано к изданию методической комиссией факультета землеустройства и лесного хозяйства (протокол № 1 от 03. 09. 2012 г.)

Составители: доцент Ишбулатов М.Г., ст. преп. Яковлева Ю.Н.

Рецензент: доцент, к.т.н. Лемешев А.И.

Ответственный за выпуск: заведующий кафедрой кадастра

недвижимости и геодезии, к.с-х..н., доцент Ишбулатов М.Г.,

 

 

 

г. Уфа, БГАУ, кафедра кадастра недвижимости и геодезии

Общие сведения

Съемочная сеть, делится на плановую и высотную.

Плановая высотная сет в зарыто местности строится в виде отдельных теодолитных ходов или систем теодолитных ходов, опирающихся на пункты исходной геодезической сети, а также в виде свободных сетей теодолитных полигонов.

Высотная геодезическая сеть строится методом геометрического или тригонометрического нивелирования. Она может состоять из отдельных нивелирных ходов или систем нивелирных ходов, опирающихся на пункты исходной высотной сети более высокого класса, а также в виде сетей свободных полигонов.

При уравновешивании несвободных съемочных сетей координаты или отметки пунктов исходной сети должны быть известны, при этом они рассматриваются как безошибочные и не подлежат исправлению. Поэтому такие пункты часто называют твердыми.

Рассмотрим уравновешивание свободных и несвободных сетей ходов. Для этих сетей существуют различные способы уравновешивания.

 

Уравнивание системы нивелирных ходов с одной узловой точки

Требуется уравновесить систему нивелирных ходов с одной узловой точки по рисунку 1, опирающуюся на пункты нивелирования ранее построенной сети более высокого класса, если известны: отметки исходных пунктов На, Нв, Нд, суммы измеренных превышений по ходам h₁ h₂, h_3, длина ходов L₁ L₂,L_3.

 

Рисунок 1 Схема нивелирных ходов

Составляется схема ходов, и вычисляются невязки с суммой превышений по наиболее коротким ходам. Для определения достоверности вычисляют допустимую невязку по формуле 2.1..

fh =±20 мм л/Z (2.1)

где Z - длина хода (км).

Определяется отметка узловой точки по каждому ходу.

Нк²=На + h₁, Нк² = Нв + h₂, Нк³=Нд+h₃

Для нивелирного хода определяется вес.

P₁ = С/ L₁ , P₂ = С/ L₂, Р₃ = С/ L₂

Средне весовое значение отметки определяется формулой 2.2.

(2.2)

где

Вычисляются невязки превышений по каждому ходу.

fh₁ = h₁-(H - Ha)

fh₂ = h₂- (Н - Нв)

fh₃ = h₃- (Н - Нд)

Полученные невязки распределяются на превышения соответствующих
ходов и определяются отметки точек.

Проверка: [рf]=0

Производится оценка точностей полевых работ, определяется средняя квадратическая погрешность единицы веса по формуле 2.3.

(2.3)

где N - количество ходов

Средняя квадратическая погрешность определения узловой точки определяется по формуле 2.4.

(2.4)

Н = Нк±М

3 Уравнивание теодолитных ходов с одной узловой точки

Требуется уравнять систему теодолитных ходов с одной узловой точкой, опирающихся на пункты и стороны ранее построенной сети более высокого класса (рисунок 2), если известны: координаты пункты В, Д, F и дирекционные углы сторон АВ, СД, ЕF исходной сети и измеренные значения углов и длин теодолитных ходов уравниваемой системы.

Теодолитные хода уравновешивают упрощенно: вначале уравновешивают углы, затем вычисляют приращения координат, которые уравновешивают, условно считая их независимыми. Такой способ называют способом раздельного уравнивания.

 

 

Рисунок 2 Схема теодолитных ходов

Узловая сторона 2-3. Для этой линии находим значения дирекционных углов каждого хода по формуле 3.1.

α _i = α _{i исх} + 180^º · n _i - Σ β _i (3.1),

где исходной формулой будет формула 3.2

α _(n)-(n+1)= α _(n-1)-(n) + 180^º- β_n (3.2),

где α _{i исх} = α _АВ ;α _СД; α _ЕF

По найденным значениям α находят угловые невязки по формулам 3.3, по ходам заключенными между исходными дирекционными углами, выбираем два хода с наименьшим числом углов.

f_{β (1+2)} = α ₂ - α ₁; f_{β (2+3)} = α ₃ - α ₂ (3.3)

Если полученные невязки оказываются допустимыми, то определяют вес каждого направления на основании формулы 3.4

P_i = k / n₁ (3.4)

где n– количество углов, k = const.

По формуле 3.5 вычисляют средне весовое значение дирекционного угла узловой линии.

α = = α ₀ + (3.5)

α ₀ - приближенное значение, ε _i = α _i - α ₀

Вычисление невязок, по ходам 1, 2, 3 по формуле 3.6

f _β = Σ β _пр – Σ β _теор (3.6)

Σ β _теор = (для разомкнутого хода) = α _нач + 180^°·n – α _кон

f _βi = Σ β_i – ( α _нач + 180^°·n – α _кон ) или

f _βi = α – ( α_{i исх} + 180^°·n – Σ β_{i исх} ) или f _βi = α – α_i

f _βi = α – α_i – если в формуле применялись измеренные правые по ходу углы

f _βi = α_i – α – если в формуле применялись измеренные левые по ходу углы

Контролем правильности вычисления дирекционного угла α и невязки f_βi является формула: [ p f _β] = 0

Если невязки являются допустимыми, их распределяют с противоположным знаком в соответствующие ходы (поровну на каждый угол).

Вычисляют дирекционные углы всех сторон.

Средняя квадратическая ошибка измеренного угла определяется по формуле 3.7:

m = (3.7)

Средне квадратическая ошибка единицы веса определяется формулой 3.8:

μ = 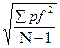(3.8)

где N– число ходов.

При малом количестве числа ходов оценка точности является грубой.

По вычисленным дирекционным углам и длинам сторон вычисляют приращение координат и их суммы по ходам. Уравнивание приращений координат производится, так же как и уравнивание углов.

х_i = х_{i исх} + ΣΔх_i у_i = у_{i исх} + ΣΔу_i

где х_{i исх} = х_в; х_д; х_F у_{i исх} = у_в; у_д; у_F

Для проверки правильности линейных измерений вычисляют невязки, по двум наиболее коротким ходам.

f_{x (1 – 2)} = х₂ - х₁ ; f_{у (1 – 2)} = у₂ - у₁

f_{x (2 – 3)} = х₃ - х₂ ; f_{у (2 – 3)} = у₃ - у₂

Абсолютная невязка

f_{абс 1+2} = √ f _х² ₁₊₂ + f _у² ₁₊₂ ; f_{абс 1+2} = √ f _х² ₁₊₂ + f _у² ₁₊₂

Относительная невязка

f_{отн 1+2} = f _{абс 1+2} / L ₁₊₂ ; f_{отн 2+3} = f _{абс 2+3} / L ₂₊₃

Если невязка допустима, вычисляют веса, для каждого значения координат узловой точки.

P_i = K / L_{i( расстояние)}

у= 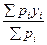= у₀ + 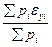; х= = x₀ +

По этим координатам вычисляют невязки приращения по каждому ходу

f_хi = х_i – х; f_уi = у_i – у

Правильность вычисления окончательных координат узловой точки и невязку приращения координат, определяется по формуле:

[ p f x ] = 0; [ p f у ] = 0

Полученные невязки с противоположным знаком распределяются на приращения соответствующих ходов, пропорционально длинам этих ходов. После распределения невязок вычисляют координаты всех вершин теодолитных ходов.

 

Приложение А

Таблица 1 Варианты уравнивания нивелирной сети с одной узловой точкой

Вариант	Реперы	Превышения	Расстояния
Pn 10	Pn ll	Pn l2	h 1	h 2	h 3	L 1	L 2	L 3
	101,242	151,278	136,539	28,111	-21,921	-7,182	3,9	4,4	4,2
	139,567	125,872	137,939	-10,182	3,599	-8,554	3,7	4,2	4,3
	123,829	132,534	121,765	5,519	-3,142	7,638	4,0	4,1	4,2
	117,678	129,975	102,761	-1,795	-14,065	13,121	3,1	3,9	3,6
	126,721	101,975	103,761	-10,839	13,909	12,122	3,8	4,1	3,7
	135,562	115,782	112,781	-13,782	5,997	8,997	3,7	1,0	4,1
	129,781	134,642	102,698	-8,007	-12,891	19,052	3,9	4,2	4,1
	101,597	136,246	145,756	20,149	-14,471	-23,980	4,1	4,0
	159,761	161,523	127,693	-17,421	-19,182	14,678	3,8	4,3	4,2
	160,843	131,372	126,593	-18,497	10,971	15,748	3,6	3,9	3,5
	25,92	27,861	32,676	4,669	2,721	-2,095	3,2	4,1	3,6
	28,21	31,672	54.925	2,489	-1,062	-4,235	3,5	4,2	3,3
	34,26	32,821	28,563	-4,142	-2,239	2,018	3,8	4,0	4,1
	58,263	62,973	52,821	-1,468	-6,198	3,981	4,0	3,9	3,9
	66,627	59,947	51,088	-3,838	-3,145	5,719	3,7	4,1	3,3
	51,623	46,264	41,889	-5,921	-0,581	3,812	3,4	3,9	4,1
	40,005	43,580	50,989	5,695	2.115	-5,312	3,6	3,2	3,8
	151,621	124,735	132,534	-11,050	15,830	8,032	2,8	3,1	2,7
	79,777	65,621	64,328	-7,650	1 6,505	7,810	3,2	2,9	3,6
	98,126	102,435	105,272	14,340	10,035	7,200	2,5	3,0	3,2
	103,626	107,534	112,439	-3,630	-7,542	-12,450	3,1	3,2	3,7
	83,555	94,121	80,666	12,340	1,772	15,226	3,1	3,5	2,6
	41,333	43,222	50,721	8,560	6,672	-0,837	3,2	3,7	3.1
	54,768	56,852	59,747	5,680	3,590	0,697	4,2	3,8	2,6
	99,999	100,500	87,645	-10,005	-10,510	2,350	3,6	3,7	3,8
	74,688	82,539	76,561	10,320	2,460	8,448	3,9	2,1	3,7
	80,532	85,679	73,468	1,460	-3,685	8,530	3,4	3,3	2,6
	120,571	130,232	122,643	4,436	-5,230	2,366	3,4	2,8	3,6
	40,263	37,563	48,711	-6,036	15,123	2,418	3,2	4,1	2,9
	70,325	62,888	60,222	4,470	2.972	+5,628	5,1	4,2	4,3
	81,232	71,242	80,335	-3,082	6,000	-3,981	4,8	5,2	3,9
	38,262	44,356	46,555	-4,637	-2,428	3,666	3,8	2,6	2,5
	41,444	49,566	40,838	3,956	-4,780	3,336	6,4	5,2	4.3

 

Библиографический список

1. Маслов А.В. и др. Геодезия. – М.: Недра, 1980. – 528 с.

2. Баканова В.В. и др. Практикум по геодезии. – М.: Недра, 1983.– 240 с.

3. Шестюков А.Д., Баканова А.И. Справочное пособие по геодезическим работам при возведении гидротехнических сооружений. М.: Недра,

1990, стр. 96-98.