 |
Главная |
Тема 9. Классическое исчисление предикатов
|
из
5.00
|
Изучив материалы темы, Вы сможете:
- понять, что такое исчисление предикатов;
- применять метод аналитических таблиц для обоснования общезначимости формул исчисления предикатов;
- перечислить правила редукции;
- уяснить смыл свободных и связанных переменных;
- записать предложение, используя язык исчисления предикатов.
Исчисление предикатов – раздел математической логики, исследующий операции с высказываниями, расчленёнными на субъект и предикат.
Алфавит языка логики предикатов образуется присоединением к алфавиту языка логики высказываний следующих знаков:
а) квантор всеобщности  (читается – все, всякий, каков бы ни был и т.д.); квантор существования
(читается – все, всякий, каков бы ни был и т.д.); квантор существования  (читается – некоторые, хотя бы один, существует и т.д.).
(читается – некоторые, хотя бы один, существует и т.д.).
б) предметные или индивидные переменные  ;
;
в) символы n-местных (n= 1, 2…) предикатов, или n-местные предикатные буквы. Символы одноместных предикатов  и т.д.
и т.д.
В предикатных буквах верхний индекс указывает число их (аргументных) мест, а нижние индексы служат для различения предикатных букв с одинаковым числом мест.
Определение предикатной формулы.
1. а) пропозициональная буква есть формула;
б) выражение, состоящее из n-местной предикатной буквы с приписанной справа n-членной последовательностью предметных переменных, есть формула;
2. а) если А, В – формулы, то каждое из следующих выражений: ~A, (A&B), (AvB), (A→B) есть также формула;
б) если А – формула, х – предметная переменная, то каждое из следующих выражений  и
и  есть формула.
есть формула.
в) выражение считается формулой тогда, и только тогда, когда оно может быть построено в соответствии с пп. 1-2.
Из определения непосредственно следует, что формула логики высказываний является частным случаем формулы логики предикатов, или предикатной формулы.
Формулы, определяемые в п. 1, определения предикатной формулы, называются элементарными.
Например, формулы: p, Gx, Rxy, Vxyz – элементарные формулы.
Элементарная формула с одноместной предикатной буквой, например, формула Gx, читается: «х обладает свойством G», или «G от х»; элементарная формула с двухместной предикатной буквой, например, Rxy читается: «х находится в отношении R к y», или «R от x, y»; элементарная формула с трёхместной предикатной буквой, например, Vxyz может быть прочитана: «x, y, z находятся в отношении V», или «V от x, y, z» и т.п.
Иногда переменные, стоящие после предикатной буквы, заключают в скобки и разделяют запятыми. Так, вместо Vxyz можно было бы написать V (x, y, z). Кроме того, элементарные формулы с двухместными предикатными буквами записываются так: первую переменную ставят перед предикатной буквой, а вторую – после неё. Например, вместо Rxy пишут xRy.
При построении выводов и доказательств средствами логики предикатов основную роль играют понятия свободных и связанных вхождений переменных в формуле.
Определение свободных и связанных вхождений переменных в формуле F.
1. F есть элементарная формула:
а) в F нет ни свободных, ни связанных переменных, если F – пропозициональная буква;
б) в F все вхождения переменных свободны, если F не является пропозициональной буквой.
2. F не есть элементарная формула:
а) формулу F можно представить в одном из следующих видов: ~A, A&B, AvB, A→B, тогда в F свободны (соотв. связаны) те, и только те, вхождения переменных, которые происходят от свободных (соотв. связанных) вхождений переменных в А или В;
б) формулу F можно представить в одном из видов –  ,
,  , тогда в F: 1) все вхождения переменной х связаны; 2) вхождения остальных переменных свободны (соотв. связаны), если они происходят от свободных (соотв. связанных) вхождений переменных в А.
, тогда в F: 1) все вхождения переменной х связаны; 2) вхождения остальных переменных свободны (соотв. связаны), если они происходят от свободных (соотв. связанных) вхождений переменных в А.
Вхождение переменной х в формулу F связано, если в F оно находится в подформуле, начинающейся квантором  или
или  , за которым непосредственно следует переменная х и о котором говорят в данном случае, что он связывает переменную х.
, за которым непосредственно следует переменная х и о котором говорят в данном случае, что он связывает переменную х.
Например, в формуле

все вхождения переменной х связаны; первое и последнее вхождения переменной y свободны, остальные вхождения переменной y связаны; все вхождения переменной z свободны, единственное вхождение переменной  связано.
связано.
Параметрами формулы называют те переменные, которые имеют свободные вхождения в данной формуле. В нашем примере параметрами формулы являются y, z.
Применяя логический аппарат к анализу обычных рассуждений и к решению логических задач, важно научиться записывать предложения обычного языка с помощью логической символики.
Пример. Запишем на языке логики предикатов предложение: «Ни один человек не бессмертен». Получаем формулу:

Читается: каков бы ни был х, если х человек, то неверно, что он бессмертен.
Пример. Запишем на языке логики предикатов предложение: «Всякий студент изучает какую-нибудь науку». Получаем формулу:
 .
.
Как и в логике высказываний в логике предикатов существуют общезначимые формулы или законы логики. Общезначимая формула исчисления предикатов – тождественно-истинная, всегда-истинная формула исчисления предикатов. Иначе можно сказать, это выражения, из которых при любой подстановке значений свободных переменных получаются истинные высказывания.
Приведём некоторые общезначимые формулы исчисления предикатов:
1.  ;
;
2. 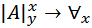 ;
;
3. 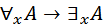 ;
;
4.  ;
;
5.  A↔
A↔  A;
A;
6. 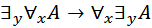 ;
;
7.  ;
;
8.  , где х не входит свободно в А;
, где х не входит свободно в А;
9.  ;
;
10.  , где х не входит свободно в В;
, где х не входит свободно в В;
11.  ;
;
12.  , где х не входит свободно в А;
, где х не входит свободно в А;
13.  ;
;
14.  ,где х не входит свободно в А;
,где х не входит свободно в А;
15. 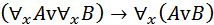 ;
;
16.  ;
;
17.  , где х не входит свободно в А;
, где х не входит свободно в А;
18.  , где х не входит свободно в А;
, где х не входит свободно в А;
19.  A;
A;
20. 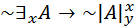 ;
;
21.  ;
;
22.  A
A  ;
;
23.  ;
;
24.  ;
;
25. 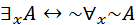 ;
;
26.  ;
;
27.  , где х не входит свободно в А;
, где х не входит свободно в А;
28. 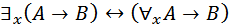 , где х не входит свободно в В;
, где х не входит свободно в В;
29.  , где х не входит свободно в А.
, где х не входит свободно в А.
Для обоснования общезначимости формул и наличия отношения логического следования существует, так называемый метод аналитических таблиц.
Аналитической таблицей называется конечная или бесконечная последовательность строк  , …, в которой каждая строка
, …, в которой каждая строка  содержит конечное число списков формул языка логики предикатов. Каждая последующая строка
содержит конечное число списков формул языка логики предикатов. Каждая последующая строка  получается из предшествующей
получается из предшествующей  заменой какого-нибудь списка формул на один или два новых списка формул на основании некоторого правила редукции.
заменой какого-нибудь списка формул на один или два новых списка формул на основании некоторого правила редукции.
Список формул называется замкнутым, если в его составе имеется некоторая формула С и её отрицание ~С.
Аналитическая таблица называется замкнутой, если она содержит конечное число строк и каждый список формул, находящийся в последней строке таблицы, является замкнутым.
Формула А общезначима (╞ А), если и только если существует замкнутая аналитическая таблица, первая строка которой содержит единственный список формул, состоящий из одной формулы – формулы ~A.
Из формул  логически следует формула В (
логически следует формула В (  ╞ В), если существует замкнутая аналитическая таблица, первая строка которой содержит единственный список формул, состоящий из формул
╞ В), если существует замкнутая аналитическая таблица, первая строка которой содержит единственный список формул, состоящий из формул  , ~B.
, ~B.
Правила редукции:
Γ, Α&Β, Δ [&]
Γ, Α, B, Δ
Γ– последовательность (возможно, пустая) формул, предшествующих Α&Β, а Δ – последовательность (возможно, пустая) формул, следующих за Α&Β.
Γ‚~(A&B)‚Δ [~&]
Γ‚~Α‚Δ|Γ‚~Β‚Δ
Γ‚ΑvB‚Δ [v]
Γ‚Α‚Δ|Γ‚B‚Δ
Γ‚~(AvB)‚Δ [~v]
Γ‚~A‚~Β‚Δ
Γ‚Α→B‚Δ[→]
Γ‚~A‚Δ|Γ‚B‚Δ
Γ‚~(A→Β)‚Δ[~→]
Γ‚Α‚~Β‚Δ
Γ‚~~Α‚Δ[~~]
Γ‚Α‚Δ
Γ‚ 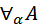 ‚Δ [
‚Δ [  ] ,
] ,
Γ‚ 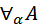 ‚Α(t)‚Δ
‚Α(t)‚Δ
где А(t) – результат замены всех свободных вхождений α в А на произвольный замкнутый терм t.
Γ‚~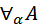 ‚Δ [~
‚Δ [~  ]
]
Γ‚~Α(k)‚Δ
где Α(k) – результат замены всех свободных вхождений α в А на предметную константу k, которая не содержится в верхнем списке.
Γ‚  ‚Δ [
‚Δ [  ]
]
Γ‚A(k)‚Δ
где Α(k) – результат замены всех свободных вхождений α в А на предметную константу k, которая не содержится в верхнем списке.
Γ‚~ ‚Δ [~
‚Δ [~ ]
]
Γ‚~ ‚~Α(t)‚Δ
‚~Α(t)‚Δ
где А(t) – результат замены всех свободных вхождений α в А на произвольный замкнутый терм t.
Рассмотрим на примере метод построения аналитических таблиц.
Пример. Обоснуем общезначимость формулы

Строим аналитическую таблицу:

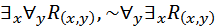 [~ →]
[~ →]
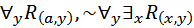 [
[ ]
]
 [~
[~  ]
]
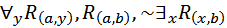 [
[  ]
]
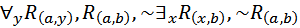 [~
[~ ].
].
Аналитическая таблица представляет собой некоторую последовательность шагов, которая представляет собой рассуждение от противного. Поэтому в первой строке таблицы записывается формула, противоречащая исходной формуле. Последняя строка должна содержать противоречие, то есть формулу С и её отрицание ~С. В нашем примере единственный формульный список последней строки содержит формулу 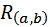 вместе с её отрицанием ~
вместе с её отрицанием ~ 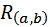 , поэтому аналитическая таблица замкнута и формула
, поэтому аналитическая таблица замкнута и формула  общезначима. В строке 3 мы применяем правило [
общезначима. В строке 3 мы применяем правило [ ] и заменяем свободные вхождения в
] и заменяем свободные вхождения в  переменной х на предметную константу а. В строке 4 применяем правило [~
переменной х на предметную константу а. В строке 4 применяем правило [~  ], переменную у, стоящую за
], переменную у, стоящую за  в формуле
в формуле
 заменяем константой, не встречающейся в единственном списке формул строки 3, то есть любой константой, кроме а, скажем b. Потом применяем правило [
заменяем константой, не встречающейся в единственном списке формул строки 3, то есть любой константой, кроме а, скажем b. Потом применяем правило [  ] , в результате должна сохраниться формула
] , в результате должна сохраниться формула  и добавиться формула
и добавиться формула  , где t – любой замкнутый терм. В формульном списке строки 4 содержатся два замкнутых терма – константы а и b. Выбираем из них b, так как это поможет нам достигнуть цели –получения в формульном списке формул вида С и ~С. Применяя правило [~
, где t – любой замкнутый терм. В формульном списке строки 4 содержатся два замкнутых терма – константы а и b. Выбираем из них b, так как это поможет нам достигнуть цели –получения в формульном списке формул вида С и ~С. Применяя правило [~ ], сохраняем формулу
], сохраняем формулу  и к списку формул добавляем
и к списку формул добавляем 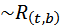 , где t – произвольный замкнутый терм. Заменяем t на константу а.
, где t – произвольный замкнутый терм. Заменяем t на константу а.
В ряде случаев построенная аналитическая таблица может свидетельствовать о необщезначимости некоторой формулы А или о том, что из  не следует логически В. Это имеет место в том случае, когда первая строка таблицы включает единственный список, состоящий из формулы ~Α (или из формул
не следует логически В. Это имеет место в том случае, когда первая строка таблицы включает единственный список, состоящий из формулы ~Α (или из формул  , ~B), а сама таблица незамкнута, но содержит конечное число строк и к формульным спискам последней строки нельзя применить никакое правило редукции.
, ~B), а сама таблица незамкнута, но содержит конечное число строк и к формульным спискам последней строки нельзя применить никакое правило редукции.
Контрольные вопросы:
1. Дайте определение классическому исчислению предикатов.
2. Что такое свободные и связанные переменные?
3. Как можно обосновать общезначимость формулы исчисления предикатов?
4. Какую роль выполняют кванторы всеобщности и существования в формулах исчисления предикатов?
5. Дайте определение предикатной формулы.
6. При каких условиях аналитическая таблица считается замкнутой?
|
из
5.00
|
Обсуждение в статье: Тема 9. Классическое исчисление предикатов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

