 |
Главная |
Соотношение неопределенностей
|
из
5.00
|
Пусть материальная точка массы m движется вдоль оси x. В некоторый момент времени она занимает место с координатой x и обладает определенным импульсом  . Спустя некоторое время частиц имеет x1 и p1. Совокупность последовательных положений движущейся точки образует траекторию ее движения. Если известны силы
. Спустя некоторое время частиц имеет x1 и p1. Совокупность последовательных положений движущейся точки образует траекторию ее движения. Если известны силы  , действующие на материальную точку, то по второму закону Ньютона можно рассчитать все последовательные координаты X и значения импульса Р:
, действующие на материальную точку, то по второму закону Ньютона можно рассчитать все последовательные координаты X и значения импульса Р:


Эти выражения представляют собой принцип причинности в классической механике: если известны силы Fx , действующие на материальную точку, то из них можно определить приращения ее координаты (dx) и импульса (dpx) в последовательные промежутки времени и тем самым рассчитать все ее движение.То есть:
· Материальная точка обладает одновременно определенными значениями координаты и импульса.
· Совокупность последовательных положений движущейся точки образует определенную линию в пространстве – траекторию.
· Принцип причинности позволяет определить положение и импульс движущейся точки на ее траектории в любой последовательный момент времени.
Принципиально иначе обстоит дело с локализацией волновых процессов.
1. Волна – протяженный объект, заполняющий определенную область пространства, а не сосредоточенный в одной точке с координатой  .
.
Для упрощения рассмотрим одномерное распространение волны вдоль оси Х. Любая волна характеризуется волновой функцией  . В нашем случае Y - функция двух переменных:
. В нашем случае Y - функция двух переменных:

 Локализация волновой функции в пространстве может быть различной. Простейшая монохроматическая волна, распространяющаяся вдоль оси Х, показана на рис.22 (мгновенный снимок). Пунктиром показано положение волны через некоторый промежуток времени. Такая волна заполняет все бесконечное пространство. Интервал координат
Локализация волновой функции в пространстве может быть различной. Простейшая монохроматическая волна, распространяющаяся вдоль оси Х, показана на рис.22 (мгновенный снимок). Пунктиром показано положение волны через некоторый промежуток времени. Такая волна заполняет все бесконечное пространство. Интервал координат  , в котором заключен волновой отрезок, равен бесконечности.
, в котором заключен волновой отрезок, равен бесконечности.
Для электронных волн  . Т.к. для монохроматической волны l является постоянной, то ей отвечает вполне определенное значение импульса, т.е.
. Т.к. для монохроматической волны l является постоянной, то ей отвечает вполне определенное значение импульса, т.е.  , в котором заключены возможные значения импульса, равно нулю. Следовательно, чисто монохроматическая волна характеризуется:
, в котором заключены возможные значения импульса, равно нулю. Следовательно, чисто монохроматическая волна характеризуется:

Следовательно, такой волновой объект имеет вполне определенный импульс (  ) и совершенно неопределенную координату (
) и совершенно неопределенную координату (  ) - область локализации .
) - область локализации .
2. Волновой пакет - волна, локализованная в некотором интервале  , отличная от нуля внутри этого интервала и практически равная нулю вне интервала
, отличная от нуля внутри этого интервала и практически равная нулю вне интервала  . Эта суперпозиция монохроматических волн с различными значениями l, рис.22.
. Эта суперпозиция монохроматических волн с различными значениями l, рис.22.
 На рис.23 (А) показан набор таких волн с различными длинами волн, от l до l+Dl представляющий собой волновой пакет, рис.23 (Б). Результирующая волновая функция практически отлична от нуля в некотором интервале Dх. Однако при такой пространственной локализации волны начинают терять определенность понятия длины волны, а значит и импульса Р частицы, связанного с волной. Волновой пакет это набор монохроматических волн, импульсы которых заключены в интервале:
На рис.23 (А) показан набор таких волн с различными длинами волн, от l до l+Dl представляющий собой волновой пакет, рис.23 (Б). Результирующая волновая функция практически отлична от нуля в некотором интервале Dх. Однако при такой пространственной локализации волны начинают терять определенность понятия длины волны, а значит и импульса Р частицы, связанного с волной. Волновой пакет это набор монохроматических волн, импульсы которых заключены в интервале: 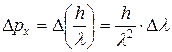 .
.
Чем в более узком интервале локализована волна, тем более широкий интервал для интерферирующих волн (а, следовательно, и интервал импульсов  ) входит в пакет, представляющий эту волну. Следовательно, увеличение определенности в локализации волн (уменьшение
) входит в пакет, представляющий эту волну. Следовательно, увеличение определенности в локализации волн (уменьшение  ) связано с одновременным возрастанием неопределенности
) связано с одновременным возрастанием неопределенности  . В пределе:
. В пределе:

Такой волновой пакет имеет вполне определенную координату  , но совершенно неопределенный импульс.
, но совершенно неопределенный импульс.
На рис.23 показан набор таких волн с различными длинами волн, от l до l+Dl представляющий собой волновой пакет. Результирующая волновая функция практически отлична от нуля в некотором интервале  . Однако при такой пространственной локализации волны начинают терять определенность понятия длины волны, а значит и импульса Р частицы, связанного с волной. Волновой пакет это набор монохроматических волн, импульсы которых заключены в интервале:
. Однако при такой пространственной локализации волны начинают терять определенность понятия длины волны, а значит и импульса Р частицы, связанного с волной. Волновой пакет это набор монохроматических волн, импульсы которых заключены в интервале:
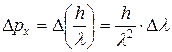
С электроном отождествляется волна де Бройля, для которой справедливы все приведенные выше рассуждения. Следовательно: Электрон, так же как и фотон, не может иметь одновременно определенную координату х и импульс Рx.1
Соотношение между  и
и  проанализировал впервые Гейзенберг. Он исходил из серии "мысленных" опытов. Давайте рассмотрим один из этих опытов.
проанализировал впервые Гейзенберг. Он исходил из серии "мысленных" опытов. Давайте рассмотрим один из этих опытов.
Чтобы определить положение и импульс электрона, нужно "осветить" его и получить хотя бы один рассеянный при столкновении фотон. При этом, вследствие дифракции, точность в определении координаты электрона не может быть больше длины волны излучения:  . Чем точнее нужно измерить положение электрона, тем меньше должно быть l. Но при рассеянии фотона электрон получает отдачу и его импульс меняется на величину
. Чем точнее нужно измерить положение электрона, тем меньше должно быть l. Но при рассеянии фотона электрон получает отдачу и его импульс меняется на величину  порядка импульса фотона:
порядка импульса фотона:  , что и составит погрешность в определении его импульса.
, что и составит погрешность в определении его импульса.
Следовательно:  .
.
Аналогично и для других координат:  . Это соотношение показывает, что с увеличением массы ограничения, вносимые ими в возможность применения классических понятий координаты и скорости, уменьшаются.
. Это соотношение показывает, что с увеличением массы ограничения, вносимые ими в возможность применения классических понятий координаты и скорости, уменьшаются.
В самом деле, ввиду малости h, неопределенности в значениях координаты и скорости из формулы:  становятся пренебрежительно малыми у тел с m, во много раз большей масс частиц, находящихся в атоме.
становятся пренебрежительно малыми у тел с m, во много раз большей масс частиц, находящихся в атоме.
 Существуют разные способы вывода соотношения неопределенностей. Рассмотрим один из них. Предположим, рис.24, что на пути строго параллельного пучка микрочастиц с импульсом поставлен экран с узкой щелью, ширина которой в направлении оси
Существуют разные способы вывода соотношения неопределенностей. Рассмотрим один из них. Предположим, рис.24, что на пути строго параллельного пучка микрочастиц с импульсом поставлен экран с узкой щелью, ширина которой в направлении оси  -
-  . При прохождении частиц через щель происходит дифракция.
. При прохождении частиц через щель происходит дифракция.
Пусть  - угол на первый дифракционный максимум. Классическая волновая теория дает:
- угол на первый дифракционный максимум. Классическая волновая теория дает:  . Полагая
. Полагая  достаточно малым, перепишем:
достаточно малым, перепишем:  . Если теперь под величиной l понимать длину волны де Бройля (т.е. волновую характеристику микрообъекта) то можно переписать на "корпускулярном языке":
. Если теперь под величиной l понимать длину волны де Бройля (т.е. волновую характеристику микрообъекта) то можно переписать на "корпускулярном языке":
 ;
; 
Как понимать на "корпускулярном языке" сам факт существования угла  ? Очевидно, что этот факт означает, что при прохождении через щель микрообъект приобретает некоторый импульс
? Очевидно, что этот факт означает, что при прохождении через щель микрообъект приобретает некоторый импульс  в направлении оси
в направлении оси  . Легко видеть из рисунка, что
. Легко видеть из рисунка, что  . Тогда:
. Тогда:

т.е. приходим к соотношению неопределенностей.
Если в некоторый момент времени точно замерить местоположение частицы, то это уничтожит все шансы измерить ее скорость (импульс). Это в новой формулировке отражает свойственный природе дуализм волна-частица. Если решено точно измерить скорость электрона, то это позволит определить его импульс и длину волны. Длина волны электрона находится путем измерения длиной последовательности волн (длинного цуга), что отрезает путь к рассмотрению электрона в виде компактной частицы и, следовательно, его положения.
Если определяется положение, том самым подразумевается, что электрон - частица, и оставляется в стороне вопрос о его природе волновой, что уничтожает возможность что-либо сказать о его импульсе. Это результат наших попыток навязать не свойственное природе обличие. На микроскопическом уровне атомы, электроны и кванты ведут себя не как волны и не как частицы.
Соотношение неопределенностей для координаты и импульса не является единственным. Аналогичным образом связаны между собой время и энергия. Рассмотрим его следующим образом.
Неопределенность в положении регистрируемого объекта составляет, как мы уже говорили,  . Фотон (или электрон) с помощью которого происходит регистрация, движется со скоростью V и проходит отрезок, равный неопределенности в положении, за время
. Фотон (или электрон) с помощью которого происходит регистрация, движется со скоростью V и проходит отрезок, равный неопределенности в положении, за время  . Следовательно, неопределенность в моменте времени, когда объект находится в заданном положении составляет:
. Следовательно, неопределенность в моменте времени, когда объект находится в заданном положении составляет:
 .
.
Так как фотон может передать объекту либо часть совей энергии (  ), либо всю энергию, неопределенность в энергии объекта в результате равна:
), либо всю энергию, неопределенность в энергии объекта в результате равна:  . Тогда:
. Тогда: 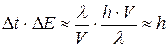
Сформулируем принцип неопределенностей в общем виде. Произведение неопределенностей значений двух канонически сопряженных переменных не может быть по порядку величины меньше постоянной Планка.
В различных источниках в правой части соотношения неопределенностей можно встретить как  , так и h и даже
, так и h и даже  . Гейзенберг со своими сотрудниками очень тщательно исследовал этот вопрос и установил, что любая из этих величин является приемлемой. Более удобно брать величину
. Гейзенберг со своими сотрудниками очень тщательно исследовал этот вопрос и установил, что любая из этих величин является приемлемой. Более удобно брать величину  Следовательно, можно записать:
Следовательно, можно записать:
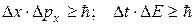
Уравнение Шредингера
Классическая механика позволяет определить положение, энергию и импульс макроскопического тела, а также их изменение. Для этого используется второй закон Ньютона:  . Ньютон постулировал этот закон, он не выводится каким-либо образом, а проверяется справедливостью решений, вытекающих из этого закона.
. Ньютон постулировал этот закон, он не выводится каким-либо образом, а проверяется справедливостью решений, вытекающих из этого закона.
В квантовой механике возникает важнейшая проблема: отыскание такого уравнения, которое являлось бы тем же, чем является уравнение движения Ньютона для классической механики. При постановке задачи описания движения частицы в пространстве и времени нужно сразу же учесть что для частицы микромира характерна двойственность свойств, которая ограничивает возможность применения к таким частицам классических понятий о координатах и скорости (импульсе). Классическому дифференциальному уравнению движения микротела квантовая механика сопоставляет линейное дифференциальное уравнение второго порядка в частных производных. Австрийский физик Шредингер (1926 г.) сопоставил движению микрочастицы комплексную функцию координат и времени - волновую функцию.
Вид волновой функции, которая характеризует состояние микрочастицы, получается из уравнения Шредингера:
 (2.4)
(2.4)
 - масса частицы;
- масса частицы;  ;
;  - оператор Лапласа:
- оператор Лапласа:
 (2.5)
(2.5)
наличие мнимой единицы "i" приводит к тому, что решение (2.4) является периодичным.  - функция координат и времени, градиент которой, взятый с обратным знаком, определяет силу, действующую на частицу. Если U не зависит от времени, то она имеет смысл потенциальной энергии частицы. Вид волновой функции определяется функцией U, то есть, в конечном счете, характером сил, действующих на частицу.
- функция координат и времени, градиент которой, взятый с обратным знаком, определяет силу, действующую на частицу. Если U не зависит от времени, то она имеет смысл потенциальной энергии частицы. Вид волновой функции определяется функцией U, то есть, в конечном счете, характером сил, действующих на частицу.
Уравнение Шредингера - основное уравнение нерелятивистской квантовой механики. Это уравнение постулируется, так же как и уравнение движения материальной точки в классической механике. Шредингер установил его из оптико-механической аналогии. Эта аналогия заключается в сходстве уравнений, описывающих траектории частиц аналитической механики с уравнениями, определяющими ход световых лучей. В оптике ход лучей удовлетворяет принципу Ферма, в механике вид траектории удовлетворяет принципу наименьшего действия.
Если силовое поле, в котором движется частица, стационарно, то U не зависит явно от времени и имеет смысл потенциальной энергии. В этом случае уравнение Шредингера распадается в решении на два сомножителя, один из которых зависит только от координат, другой только от времени:
 (2.5)
(2.5)
E - полная энергия частицы, которая в случае стационарного поля остается постоянной. Чтобы убедится в справедливости (2.5) подставим его в (2.3):

Сократим на общий сомножитель  . Тогда придем к дифференциальному уравнению, определяющему
. Тогда придем к дифференциальному уравнению, определяющему  :
:
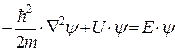 (2.6)
(2.6)
Уравнение (2.6) - уравнение Шредингера для стационарных состояний. Это уравнение можно представить в виде:
 (2.7)
(2.7)
Покажем, как можно прийти к уравнению Шредингера. Ограничимся одномерным случаем. Рассмотрим свободно движущуюся частицу. Согласно гипотезе де Бройля сопоставим ей плоскую волну, представив ее в виде:

(В квантовой механике принято брать знак минус перед показателем экспоненты). Поскольку  , то
, то
 (2.8)
(2.8)
Продифференцируем (2.8) один раз по времени, а второй раз дважды по  :
:

Тогда:

В нерелятивистской механике:

Подставим значения:
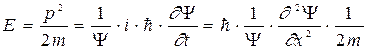
и окончательно:

Это выражение совпадает с уравнением Шредингера при U=0. Если частица движется в силовом поле, характеризуемом потенциальной энергией U, энергия и импульс связаны соотношением:
 , тогда
, тогда 
Принцип суперпозиции состояний
Своеобразие описания состояний и движений микрочастиц с помощью  - функции проявляется в правилах сложения волновых функций, выражающихся принципом суперпозиции состояний.
- функции проявляется в правилах сложения волновых функций, выражающихся принципом суперпозиции состояний.
Принцип суперпозиции в том или ином виде характерен для всех фундаментальных теорий. Так, в классической механике он приводит к векторному сложению ускорений материальной точки, вызванных одновременным действием нескольких независимых сил. В электродинамике имеет место закон векторного сложения напряженности полей, созданных различными источниками. Допустимы и обратные действия разложения сил и напряженностей на составляющие.
Принцип суперпозиции в квантовой механике состоит в следующем: пусть в данных условиях возможны различные состояния частицы (или системы частиц), описывающиеся волновыми функциями 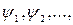 тогда возможно и состояние частицы (системы), описываемое линейной комбинацией:
тогда возможно и состояние частицы (системы), описываемое линейной комбинацией:
 (2.9)
(2.9)
где Сi – комплексные числа, удовлетворяющие условию:
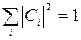

Равенство (2.9) допускает и несколько иную физическую интерпретацию, которую можно считать второй частью содержания принципа суперпозиции: пусть в данных условиях частица (система) описывается волновой функцией  и при этом справедливо равенство (2.9). Тогда частица (система) с вероятностью
и при этом справедливо равенство (2.9). Тогда частица (система) с вероятностью  , равной
, равной  , находится (может быть обнаружена) в состоянии
, находится (может быть обнаружена) в состоянии  . Согласно этой формулировке, состояния
. Согласно этой формулировке, состояния  при данных условиях образуют альтернативный ряд состояний и частица находится в том или ином из них с определенной вероятностью
при данных условиях образуют альтернативный ряд состояний и частица находится в том или ином из них с определенной вероятностью  .
.
Рассмотрим мысленный опыт – дифракцию частиц на двух отверстиях. Казалось бы, что каждый электрон, проходит через одно отверстие; поэтому на экране появится дифракционная картина, которая получится в результате простого наложения картин дифракции на первом и втором отверстии. Однако картина, получаемая при дифракции электронов на двух щелях, имеет вид колец, расположенных вокруг центрального максимума. На рис.25 изображена соответствующая диаграмма распределения интенсивности (пунктиром на этом же рисунке показано наложение картин, образованных независимо от каждого отверстия). Она напоминает диаграмму дифракции на одном отверстии, только радиусы колец другие.
 Такой результат можно понять, если считать, что с электроном связано волновое поле. Тогда дифракция электронов происходит по тем же законам, что и дифракция электромагнитных волн. В нашем мысленном опыте картина должна совпадать с картиной дифракции света на двух отверстиях (при той же длине волны, расположении и размерах отверстий). Однако такой чисто волновой подход не исчерпывает всех сторон опыта в силу наличия корпускулярных свойств у частиц. Попробуем представить частицу в виде движущейся материальной точки. Результаты опыта можно объяснить в рамках корпускулярной модели, предположив, что электрон проходит сразу через два отверстия, или, проходя через одно отверстие, он каким то способом «узнает» о существовании другого отверстия, которое сказывается на его движении.
Такой результат можно понять, если считать, что с электроном связано волновое поле. Тогда дифракция электронов происходит по тем же законам, что и дифракция электромагнитных волн. В нашем мысленном опыте картина должна совпадать с картиной дифракции света на двух отверстиях (при той же длине волны, расположении и размерах отверстий). Однако такой чисто волновой подход не исчерпывает всех сторон опыта в силу наличия корпускулярных свойств у частиц. Попробуем представить частицу в виде движущейся материальной точки. Результаты опыта можно объяснить в рамках корпускулярной модели, предположив, что электрон проходит сразу через два отверстия, или, проходя через одно отверстие, он каким то способом «узнает» о существовании другого отверстия, которое сказывается на его движении.
Основываясь на этом мысленном опыте, покажем, в каком отношении между собой находятся волновая природа микрочастиц и принцип суперпозиции состояний.
Пусть сначала открыто одно из отверстий и закрыто другое – получается одна дифракционная картина на экране. Затем закроем первое отверстие и откроем второе – получим другую дифракционную картину. Третья дифракционная картина получится при обоих открытых отверстиях. Если бы речь шла не о микрочастицах, а о движущихся по законам классической механики малых телах – корпускулах, то каждое тело проходило бы через одно отверстие вне зависимости от наличия другого отверстия. Поэтому дифракционная картина при обоих открытых отверстиях была бы простым наложением друг на друга картин дифракций, полученных на каждом из отверстий по отдельности.
Однако для микрочастиц опыт обнаруживает дифракцию на двух отверстиях с картиной распределения максимумов и минимумов, отличной от простого наложения картин дифракции только от первого отверстия и только от второго. Это новая дифракционная картина.
Результаты опыта в квантовой механике объясняются с помощью принципа суперпозиции. Пусть 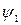 - функция состояния, соответствующая одному открытому отверстию, а
- функция состояния, соответствующая одному открытому отверстию, а  - другому. Плотности вероятностей, определяющие дифракционную картину в каждом случае, определяются функциями:
- другому. Плотности вероятностей, определяющие дифракционную картину в каждом случае, определяются функциями:

При обоих открытых отверстиях функция состояния находится как сумма 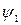 и
и  :
:
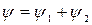
Но теперь ей соответствует новое распределение вероятности:

причем

Именно потому, что складываются волновые функции, а не вероятности, и возникает новая дифракционная картина – результат интерференции волн 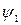 и
и  .
.
Сложение волновых функций, а не вероятностей – важнейшая особенность суперпозиции состояний в микромире. Благодаря этому волновая функция является исходным математическим средством описания состояния микрочастиц.
Операторы
Очень важным в физике микромира является понятие среднего значения. Рассмотрим в качестве примера N молекул, движущихся с разными скоростями и, следовательно, имеющих разные значения энергии. Среднее значение энергии тогда определится:
 (2.10)
(2.10)
Другой способ определения средней энергии заключается в следующем.
Найдем число молекул  , энергия которых заключена между
, энергия которых заключена между 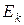 и
и  . Произведем подсчет для всех значений энергии. Сумма, стоящая в выражении (2.10), тогда запишется:
. Произведем подсчет для всех значений энергии. Сумма, стоящая в выражении (2.10), тогда запишется:

Эта формула не является вполне точной, так как непрерывно меняющуюся энергию мы заменили дискретным набором 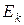 . Однако при достаточно мелком разбиении эта неточность может быть сделана сколь угодно малой.
. Однако при достаточно мелком разбиении эта неточность может быть сделана сколь угодно малой.
Тогда формула для определения средней энергии принимает вид:
 (2.11)
(2.11)
 определяет долю молекул, энергия которых лежит в k-ом интервале или, что тоже самое, вероятность молекуле иметь заданную энергию
определяет долю молекул, энергия которых лежит в k-ом интервале или, что тоже самое, вероятность молекуле иметь заданную энергию 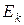 (заметим, что сумма всех вероятностей, как всегда равна единице
(заметим, что сумма всех вероятностей, как всегда равна единице  ).
).
При непрерывном распределении вероятности попасть в бесконечно малый интервал между  и
и  зависит от выбранного значения
зависит от выбранного значения  и от ширины интервала
и от ширины интервала  и обозначается поэтому
и обозначается поэтому  . Функция
. Функция  , определяющая в нашем случае распределение молекул по энергиям имеет максимальное значение вблизи какого-то значения Е и падает как при увеличении так и при уменьшении энергии от этого выбранного значения. Функция
, определяющая в нашем случае распределение молекул по энергиям имеет максимальное значение вблизи какого-то значения Е и падает как при увеличении так и при уменьшении энергии от этого выбранного значения. Функция  носит название плотность вероятности.
носит название плотность вероятности.
При непрерывных распределениях сумма (2.11) должна быть заменена интегралом:
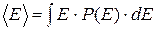 (2.12)
(2.12)
Интеграл (10) берется по всем возможным значениям энергии от  до
до  , или от
, или от  до
до  . В общем случае, когда имеется среднее значение какой-то величины
. В общем случае, когда имеется среднее значение какой-то величины  , плотность вероятности обозначается
, плотность вероятности обозначается  .
.
Перейдем теперь к задаче об определении среднего значения координаты  для микрочастицы, обладающей волновой функцией
для микрочастицы, обладающей волновой функцией  . Квадрат модуля волновой функции, как мы уже говорили, является плотностью вероятности нахождения частицы в окрестности
. Квадрат модуля волновой функции, как мы уже говорили, является плотностью вероятности нахождения частицы в окрестности  . Согласно (2.12) среднее значение координаты будет:
. Согласно (2.12) среднее значение координаты будет:

или
 (2.13)
(2.13)
Повторяя проведенные рассуждения для вычисления среднего значения  , нетрудно убедится, что:
, нетрудно убедится, что:


и, что вообще, среднее значение любой функции  равно:
равно:
 (2.14)
(2.14)
Общее утверждение квантовой механики заключается в том, что среднее значение любой физической величины 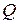 находится по формуле:
находится по формуле:
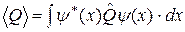 (2.15)
(2.15)
где  - оператор физической величины
- оператор физической величины 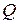 . Сравнение формул (2.13), (2.14) с (2.15) показывает, что оператор
. Сравнение формул (2.13), (2.14) с (2.15) показывает, что оператор  сводится к простому умножению на
сводится к простому умножению на  , а оператор
, а оператор  - к умножению на функцию
- к умножению на функцию  .
.
Оператор - это правило, посредством которого одной функции(j) сопоставляется другая функция ( 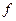 ).
).
Символически это записывается:  или
или  ,
,  - оператор. Под символом оператора скрывается совокупность действий, с помощью которых исходная функция (j) превращается в (
- оператор. Под символом оператора скрывается совокупность действий, с помощью которых исходная функция (j) превращается в (  ). Оператор может представлять собой умножение U на некоторую функцию
). Оператор может представлять собой умножение U на некоторую функцию  .
.  , т.е.
, т.е.  - оператор умножения.
- оператор умножения.
Если рассматривать U в уравнении Шредингера как оператор умножения, то ему можно придать вид:  , где
, где  - сумма операторов:
- сумма операторов:

 - оператор Гамильтона (гамильтониан) - является оператором энергии E. В квантовой механике другим динамическим переменным также сопоставляются операторы (координат, импульса, момента импульса и т.д.). Для каждой динамической переменной q составляется аналогичное уравнение:
- оператор Гамильтона (гамильтониан) - является оператором энергии E. В квантовой механике другим динамическим переменным также сопоставляются операторы (координат, импульса, момента импульса и т.д.). Для каждой динамической переменной q составляется аналогичное уравнение:  (или
(или 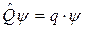 ).
).
|
из
5.00
|
Обсуждение в статье: Соотношение неопределенностей |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

