Быстрота Изменения величины

 

Среднее значение физической величины изменяется со временем по двум причинам:

1) из-за зависимости оператора величины от времени;

2) из-за некоммутативности оператора величины с гамильтонианом.

 

Оператор производной по времени. Среднее значение (2.28)

 

 

изменяется с быстротой

 

.

Учитываем уравнение Шредингера (2.54)

 

,

,

получаем

.

 

Гамильтониан эрмитовый, тогда первое слагаемое в квадратных скобках равно . Объединяем его с третьим слагаемым

. (2.66)

 

Выражение в круглой скобке по определению является оператором производной по времени

. (2.67)

 

Оператор проекции скорости. В (2.67) подставляем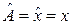

 

. (2.67а)

Используем

,

 

,

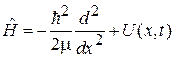находим

.

 

На практических занятии будет получено

 

,

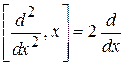тогда оператор проекции скорости

 

(2.67б)

 

удовлетворяет классическому соотношению между скоростью и импульсом, подтверждая правило соответствия.

 

Сохраняющаяся величина описывается оператором , удовлетворяющим согласно (2.67) условию

 

.

 

Если оператор не зависит от времени , тогда

 

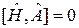. (2.68)

 

Величина сохраняется в любом состоянии, если ее оператор не зависит от времени и коммутирует с гамильтонианом.

 

Стационарное состояние характеризуется тем, что для произвольной величины a, описываемой оператором , не зависящим от времени , среднее значение постоянно

 

.

 

Даже если 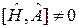, то из (2.66)

 

получаем

. (2.69)

 

В стационарном состоянии среднее значение от коммутатора оператора с гамильтонианом равно нулю.

Ток вероятности

 

Плотность вероятности обнаружения частицы около точки r

 

 

зависит от времени. Вероятность обнаружить частицу во всем пространстве неизменна

.

 

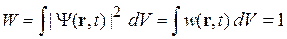Следовательно, вероятность перетекает из одного места в другое. Вводится плотность тока вероятности 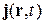и соответствующий оператор.

Умножая плотность тока вероятности j на заряд частицы e, получаем плотность электрического тока

 

,

 

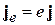вызванного движением частицы. В теории электрического тока многих частиц

,

 

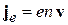где – заряд, проходящий за 1с через единичное поперечное сечение проводника; n – концентрация частиц. Тогда плотность тока вероятности для одной частицы

выражается через скорость.

 

Плотность тока вероятности. Используем оператор скорости

 

,

где

.

 

Для частицы в состоянии определяем плотность тока вероятности

 

, (2.71)

где учтено

.

 

Вектор выражаем через декартовы компоненты

 

,

где

. (2.72)

 

Уравнение непрерывности тока вероятности. Используем

 

,

 

.

 

Из уравнения Шредингера (2.54)

 

,

,

тогда

.

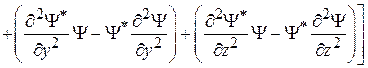Используем (2.72)

,

тогда первая круглая скобка равна и аналогично для остальных скобок. В результате получаем уравнение непрерывности

 

, (2.73)

 

где divj – дивергенция плотности тока является потоком из единичного объема. Согласно (2.73) поток из объема уменьшает вероятность в этом объеме. Следовательно, уравнение Шредингера описывает систему, у которой нет источников и стоков частиц.

 

Ток вероятности для частицы с импульсом р в состоянии плоской волны

.

Плотность вероятности

 

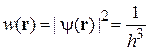
распределена равномерно по всему пространству. В состоянии равномерного движения частица обнаруживается в любой точке пространства с равной вероятностью.

Из (2.72)

находим

,

 

.

 

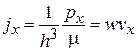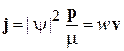Плотность электрического заряда и тока для частицы с зарядом е равны

,

.

 

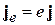При равномерном движении заряда используем 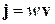и получаем известное соотношение

.

 

Из уравнения непрерывности (2.73) следует закон сохранения заряда в дифференциальной форме

.

 

Ток вероятности в стационарном состоянии. Используем (2.63)

 

,

 

где A и β – вещественные, тогда

 

.

 

Вычисляем плотность тока вероятности (2.71)

 

.

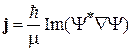Учитываем

,

получаем

.

Используя

, ,

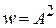находим

,

 

,

 

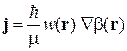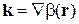. (2.74)

 

Для стационарного состояния волновой вектор равен градиенту фазы волновой функции, плотность тока вероятности пропорциональна плотности вероятности и градиенту фазы волновой функции. Если фаза b в разных точках одинаковая, то , .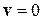

Выполняется

.

 

Для стационарного состояния поток вероятности из любого объема равен нулю.

МАТРИЦА ПЛОТНОСТИ

 

Если нет полной информации о системе, то она не имеет волновой функции и описывается матрицей плотности, введенной Л.Д. Ландау и Дж. фон Нейманом в 1927 г.

Чистое и смешанное состояния. Чистое состояние описывается волновой функцией. Для смешанного состояния известна лишь вероятность того, что состояние описывается одной из возможных волновых функций . Между этими функциями не определены фазовые соотношения и отсутствует интерференция. Например, если параметр системы измерен не точно, то состояние смешанное и является вероятностью i-ого значения параметра. Так, если в атоме водорода положение протона не фиксировано, то электрон находится в смешанном состоянии. Если протон неподвижен или его движение упорядочено, то состояние электрона чистое. Чистое состояние разлагается по ортонормированному базису с коэффициентами, которые могут регулярно изменяться. Если коэффициенты изменяются беспорядочно, то состояние смешанное. Чистое состояние переходит в смешанное в процессе декогеренциисистемы, когда она взаимодействует с объектом, испытывающим хаотические изменения, например, с макроскопическим телом. Декогеренция ускоряется с увеличением размеров квантовой системы. Система в чистом состоянии должна быть изолирована от окружающих тел и хаотически меняющихся полей путем охлаждения, вакуумирования и экранирования. Уменьшение декогеренции необходимо для квантового компьютера и квантовой криптографии. Смешанное состояние описывается матрицей плотности, чистое состояние – как волновой функцией, так и матрицей плотности.

 

Матрица плотности чистого состояния. Состояние разлагаем по собственным функциям некоторого эрмитового оператора

 

и описываем набором коэффициентов . Для среднего значения величины a получаем

, (2.76)

где

– матричный элемент оператора между состояниями и .

Определяем матрицу плотности r с элементами

 

, (2.77)

тогда

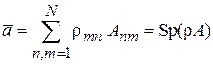, (2.78)

где

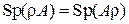– шпур (от нем. die Spur – «след») – сумма диагональных элементов матрицы;

является вероятностью обнаружения состояния в состоянии .

При получаем

,

,

где

;

 

;

 

– вероятность результата .

Наличие интерференционного слагаемого означает, что y₁ и y₂ в составе чистого состояния взаимно согласованы по фазе, т. е. когерентные. Их интерференция влияет на результат.

 

Матрица плотности смешанного состояния. Для смешанного состояния коэффициенты разложения зависят от не полностью определенного параметра состояния j. В (2.76) появляется дополнительное усреднение по j

,

 

где – вероятность j-ого значения. Определяем матрицу плотности в виде среднего по j

 

, (2.79)

тогда (2.78) сохраняет форму

 

.

Диагональный элемент

дает вероятность состояния ;

является вероятностью состояния в компоненте j смешанного состояния.

Недиагональные элементы (2.79) характеризуют корреляцию состояний m и n.

При , получаем

 

.

 

Интерференционный член отсутствует, поэтому волновые функции компонент и смешанного состоянияне когерентные.

 

Свойства матрицы плотности:

 

Условие нормировки

. (2.80)

 

Условие эрмитовости

. (2.81)

 

 

Признак чистого состояния

. (2.82)

 

При нарушении (2.82) состояние смешанное.

 

Уравнение фон Неймана

 

(2.83)

 

является аналогом уравнения Шредингера для смешанного состояния.