 |
Главная |
Типовое решение контрольной работы №4
|
из
5.00
|
Контрольная работа №1.
Задание 1. Вычислить матрицу  .
.
Задание 2. Вычислить определители.
Задание 3. Решить системы: а) методом обратной матрицы и по формулам Крамера; б) методом Гаусса. Найти общее и одно частное решение.
| № | Задание 1. | Задание 2. | Задание 3. | |||
| 1. |  , ,

| 
| 
| 
| а) 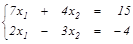 б) б) 
| |
| 2. |  , ,

| 
| 
| 
| а)  б) б) 
| |
| 3. |  , ,

| 
| 
| 
| а)  б) б) 
| |
| 4. |  , ,

| 
| 
| 
| а)  б) б) 
| |
| 5. |  , ,

| 
| 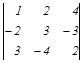
| 
| а)  б) б) 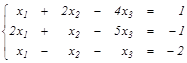
| |
| 6. |  , ,

| 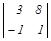
| 
| 
| а)  б) б) 
| |
| 7. |  , ,

| 
| 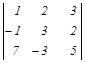
| 
| а)  б) б) 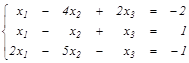
| |
| 8. |  , ,

| 
| 
| 
| а) 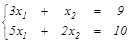 б) б) 
| |
| 9. |  , ,

| 
| 
| 
| а)  б) б) 
| |
| 10. |  , ,

| 
| 
| 
| а)  б) б) 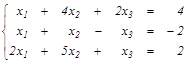
| |
КОНТРОЛЬНЫЕ ВОПРОСЫ К ЭКЗАМЕНУ
| 1. | Понятие матрицы, виды матриц. |
| 2. | Действия над матрицами. |
| 3. | Понятие определителя, минора 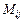 элемента элемента  матрицы матрицы  ого порядка, алгебраического дополнения ого порядка, алгебраического дополнения  элемента элемента  матрицы матрицы  ого порядка. ого порядка.
|
| 4. | Основные свойства определителей |
| 5. | Методы вычисления определителей. |
| 6. | Вычисление обратной матрицы. |
| 7. | Системы линейных уравнений: матричная запись, структура множества решений однородной и неоднородной системы. Формы записи. |
| 8. | Матричный метод решения системы линейных алгебраических уравнений. |
| 9. | Формулы Кремера для решения систем линейных уравнений с квадратной матрицей. |
| 10. | Решение систем линейных уравнений методом Гаусса. |
Контрольная работа №2.
Задание 1. Найти пределы:
Задание 2. Исследовать точки разрыва:
| Задание 1. | Задание 2. | |||||
| 1. | 
| 
| 
| 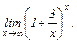
| 
| 
|
| 2. | 
| 
| 
| 
| 
| 
|
| 3. | 
| 
| 
| 
| 
| 
|
| 4. | 
| 
| 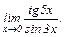
| 
| 
| 
|
| 5. | 
| 
| 
| 
| 
| 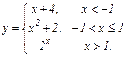
|
| 6. | 
| 
| 
| 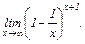
| 
| 
|
| 7. | 
| 
| 
| 
| 
| 
|
| 8. | 
| 
| 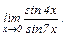
| 
| 
| 
|
| 9. | 
| 
| 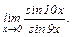
| 
| 
| 
|
| 10. | 
| 
| 
| 
| 
| 
|
КОНТРОЛЬНЫЕ ВОПРОСЫ К ЭКЗАМЕНУ
| 11. | Понятие функции (отображения). График функции. Чётность, нечётность и периодичность функции. Сложная функция. |
| 12. | Предел функции в точке. Основные теоремы о пределах Признаки существования предела |
| 13. | Предел функции на бесконечности (  ). Односторонние пределы. Замечательные пределы. ). Односторонние пределы. Замечательные пределы.
|
| 14. | Бесконечно малые и бесконечно большие функции ( Б.М.Ф и Б.Б.Ф.). Связь бесконечно большими и бесконечно малыми функциями. Сравнение бесконечно малых. |
| 15. | Непрерывность функции в точке ( на языке “ε - δ“ и на языке последовательностей). Непрерывность функции на промежутке. Свойства функций, непрерывных в точке |
| 16. | Точки разрыва функции и их классификация. |
Контрольная работа №3.
Задание 1. Найти производные функций.
Задание 2. Вычислить приближённо.
Задание 3. Исследовать функции и построить её график.
| № | Задание 1. | Задание 2. | Задание 3. | ||
| 11. | 
| 
| 
| 
| 
|
| 12. | 
| 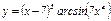
| 
| 
| 
|
| 13. | 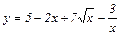
| 
| 
| 
| 
|
| 14. | 
| 
| 
| 
| 
|
| 15. | 
| 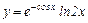
| 
| 
| 
|
| 16. | 
| 
| 
| 
| 
|
| 17. | 
| 
| 
| 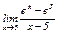
| 
|
| 18. | 
| 
| 
| 
| 
|
| 19. | 
| 
| 
| 
| 
|
| 20. | 
| 
| 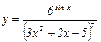
| 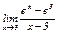
| 
|
КОНТРОЛЬНЫЕ ВОПРОСЫ К ЭКЗАМЕНУ
| 17. | Понятие производной. |
| 18. | Производная основных элементарных функций. |
| 19. | Правила дифференцирования. |
| 20. | Геометрический смысл производной. |
| 21. | Производные высших порядков. |
| 22. | Производная сложной функции. |
| 23. | Условия монотонности функции. |
| 24. | Экстремумы функции. |
| 25. | Выпуклость графика функции. Точки перегиба. |
| 26. | Асимптоты графика функции. |
| 27. | Общая схема исследования функции и построения графика. |
КОНТРОЛЬНАЯ РАБОТА №4
Задание 1. Найти интеграл, используя таблицу и основные свойства неопределённого интеграла.
Задание 2–3.Найти интеграл, используя подходящую подстановку.
Задание 4–6. Найти интеграл, используя метод интегрирования по частям.
Задание 7–11.Найти интегралы от простейших рациональных дробей.
Задание 12.Найти интегралы от иррациональных функций.
Задание 13–15.Найти интегралы от тригонометрических функций.
| Вариант № 1 | Вариант № 2 | Вариант № 3 | Вариант № 4 | Вариант № 5 | |

| 
| 
| 
| 
| |
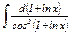
| 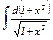
| 
| 
| 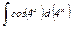
| |

| 
| 
| 
| 
| |

| 
| 
| 
| 
| |

| 
| 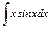
| 
| 
| |

| 
| 
| 
| 
| |

| 
| 
| 
| 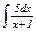
| |

| 
| 
| 
| 
| |

| 
| 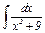
| 
| 
| |

| 
| 
| 
| 
| |

| 
| 
| 
| 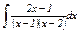
| |

| 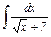
| 
| 
| 
| |

| 
| 
| 
| 
| |

| 
| 
| 
| 
| |

| 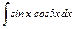
| 
| 
| 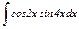
|
| Вариант № 6 | Вариант № 7 | Вариант № 8 | Вариант № 9 | Вариант № 10 | |

| 
| 
| 
| 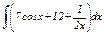
| |

| 
| 
| 
| 
| |

| 
| 
| 
| 
| |

| 
| 
| 
| 
| |

| 
| 
| 
| 
| |
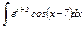
| 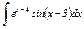
| 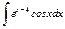
| 
| 
| |

| 
| 
| 
| 
| |

| 
| 
| 
| 
| |

| 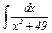
| 
| 
| 
| |

| 
| 
| 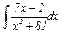
| 
| |

| 
| 
| 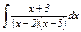
| 
| |

| 
| 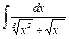
| 
| 
| |

| 
| 
| 
| 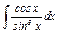
| |

| 
| 
| 
| 
| |

| 
| 
| 
| 
|
КОНТРОЛЬНЫЕ ВОПРОСЫ К ЭКЗАМЕНУ
| 1. | Понятие первообразной и неопределённого интеграла. |
| 2. | Основные свойства неопределённого интеграла. |
| 3. | Интегралы от основных элементарных функций. |
| 4. | Основные методы интегрирования. Непосредственное интегрирование. |
| 5. | Основные методы интегрирования. Интегрирование методом замены. |
| 6. | Основные методы интегрирования. Интегрирование по частям. |
| 7. | Интегрирование рациональных дробей. |
| 8. | Интегрирование простейших иррациональных дробей. |
| 9. | Интегрирование тригонометрических функций. |
| 10. | Понятие определённого интеграла. Формула Ньютона – Лейбница. |
| 11. | Основные свойства определённого интеграла. |
| 12. | Основные методы вычисление определённого интеграла. Формула Ньютона – Лейбница. |
| 13. | Геометрические приложения определённого интеграла. Вычисление площадей плоских фигур. |
| 14. | Геометрические приложения определённого интеграла. Вычисление объёмов тел вращения. |
Типовое решение контрольной работы №4
| Задание 1. Найти интеграл, используя таблицу и основные свойства неопределённого интеграла. | |
| 1. | 
|
| Задание 2–3. Найти интеграл, используя подходящую подстановку. | |
| 2. | 
|
| 3. | 
|
| Задание 4–6. Найти интеграл, используя метод интегрирования по частям. | |
| 4. | 
|
| 5. | 
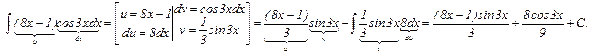
|
| 6. |  Итак, имеем:
Итак, имеем:  .
Перенося интеграл из правой части равенства в левую, получаем: .
Перенося интеграл из правой части равенства в левую, получаем:
  и окончательно имеем
и окончательно имеем 

|
| Задание 7–11. Найти интегралы от простейших рациональных дробей. | |
| 7. | 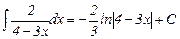
|
| 8. | 
|
| 9. | 
|
| 10. | |
| 11. | |
| 12. | |
| Задание 13–15. Найти интегралы от тригонометрических функций. | |
| 13. | 
|
| 14. | |
| 15. | 
|
КОНТРОЛЬНАЯ РАБОТА №5
Задание 1. Исследовать сходимость числовых рядов:
а) используя признак сравнения; б) по признаку Даламбера;
Задание 2. Исследовать ряд на условную и абсолютную сходимость;
Задание 3. Найти область сходимости степенного ряда.
| Задание 1 | Задание 2 | Задание 3 | ||

| 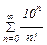
| 
| 
| |

| 
| 
| 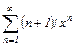
| |

| 
| 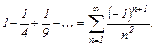
| 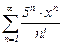
| |

| 
| 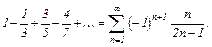
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |
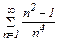
| 
| 
| 
| |

| 
| 
| 
| |

| 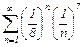
| 
| 
| |

| 
| 
| 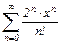
|
КОНТРОЛЬНЫЕ ВОПРОСЫ К ЭКЗАМЕНУ
| 1. | Как определяется десятая частичная сумма числового ряда? |
| 2. | Как определяется сумма числового ряда? Какой ряд называется сходящимся? |
| 3. | При каком  обобщенный гармонический ряд является сходящимся? обобщенный гармонический ряд является сходящимся?
|
| 4. | Каким будет предел общего члена сходящегося числового ряда? |
| 5. | Какие ряды выбираются в качестве эталонных при использовании признака сравнения? |
| 6. | Будет ли сходящимся ряд с положительными членами, для которого предел отношения последующего члена к предыдущему члену равен 2? |
| 7. | Предел какого выражения используется в признаке Каши? |
| 8. | Какой ряд называется знакопеременным? Какой ряд называется знакочередующимся? |
| 9. | Будет ли сходящимся знакопеременный ряд, для которого ряд из модулей его членов сходится? |
| 10. | Какой ряд называется абсолютно сходящимся? Какой ряд называется условно сходящимся? |
| 11. | Каких условий достаточно для сходимости знакочередующегося ряда? |
| 12. | Как называется множество всех  , при которых степенной ряд сходится? , при которых степенной ряд сходится?
|
| 13. | Что такое радиус сходимости степенного ряда? По какой формуле находится радиус? |
| 14. | Для какой функции можно определить ряд Тейлора? Как из ряда Тейлора можно получить ряд Маклорена? |
|
из
5.00
|
Обсуждение в статье: Типовое решение контрольной работы №4 |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

