 |
Главная |
Замена базиса и преобразование координат
|
из
5.00
|
Пусть  - п-мерное векторное пространство над полем Р и
- п-мерное векторное пространство над полем Р и  и
и  - 2 базиса
- 2 базиса  . Выразим каждый вектор (2) через вектора (1):
. Выразим каждый вектор (2) через вектора (1):

 Матрица
Матрица 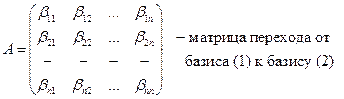
Выразим (1) через (2):

 Матрица
Матрица 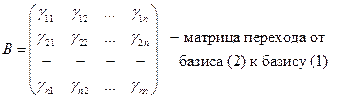
Как связаны между собой матрицы А и В? Чтобы установить это, подставим в (4) выражения из (3):
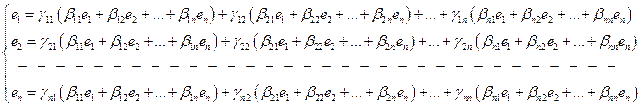


то есть  , значит матрицы перехода от базиса (1) к базису (2) и от базиса (2) к базису (1) - это взаимно обратные матрицы.
, значит матрицы перехода от базиса (1) к базису (2) и от базиса (2) к базису (1) - это взаимно обратные матрицы.
Выясним, как изменяются координаты векторов при изменении базиса.
Пусть вектор х имеет в базисах (1) и (2) координаты 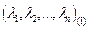 и
и  , т.е.
, т.е.  ,
,  , тогда
, тогда 


Итак, 

Теорема 3. Координаты суммы векторов в данном базисе равны сумме соответствующих координат самих векторов в этом базисе.
Доказательство: Пусть даны два вектора - х и у и в базисе  их координаты
их координаты 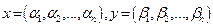 , тогда
, тогда  .
.
Значит  ,
,
т.е. координаты суммы векторов  равны
равны 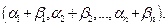 ▲.
▲.
Замечание: теорему можно расширить на любое число слагаемых векторов.
Теорема 4. Координаты произведения вектора на элемент λ поля Р в данном базисе равны произведению соответствующих координат вектора в этом базисе на элемент λ.
Доказательство: Пусть дан вектор х, имеющий в базисе  координаты
координаты  и дан
и дан  , тогда
, тогда  . Найдем координаты произведения вектора х на элемент
. Найдем координаты произведения вектора х на элемент  :
:  ,
,
т.е. координаты произведения вектора х на элемент  равны
равны  ▲.
▲.
ВОПРОС № 6 Евклидовы пространства. Ортонормированные базисы.
Опр.1. Пусть E - векторное пространство над полем действительных чисел  . Скалярным умножением в пространстве E называется отображение, ставящее в соответствие каждой паре векторов
. Скалярным умножением в пространстве E называется отображение, ставящее в соответствие каждой паре векторов  E действительное число, называемое скалярным произведением этих векторов и обозначаемое символом
E действительное число, называемое скалярным произведением этих векторов и обозначаемое символом  так, что выполняются следующие условия:
так, что выполняются следующие условия:
1.  E
E  .
.
2.  E
E  .
.
3.  E
E 
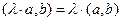 .
.
4.  E,
E, 
 .
.
Опр.2. Векторное пространство E над  , в котором определено скалярное умножение, называется евклидовым пространством.
, в котором определено скалярное умножение, называется евклидовым пространством.
Свойства скалярного умножения векторов:
1) 
 E
E  .
.
Доказательство:  ▲.
▲.
2) 
 E
E  .
.
Доказательство:  ▲.
▲.
3) 
 E .
E .
Доказательство:  E,
E,  . Тогда
. Тогда  ▲.
▲.
Примеры:
1.  .
.
2.  .
.
3. Всякое ненулевое конечномерное векторное пространство  над полем
над полем  можно превратить в евклидово пространство следующим образом: выберем в
можно превратить в евклидово пространство следующим образом: выберем в  базис, пусть этот базис -
базис, пусть этот базис -  . Тогда
. Тогда 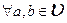
 . Формула
. Формула  определяет скалярное произведение в
определяет скалярное произведение в  .
.
Ортогональный базис
Опр.3. Векторы а и b евклидового пространства E называются ортогональными, если их скалярное произведение равно нулю.
Опр.4. Система векторов  евклидового пространства E называется ортогональной, если ортогональны любые два вектора этой системы. Система из одного ненулевого вектора считается ортогональной.
евклидового пространства E называется ортогональной, если ортогональны любые два вектора этой системы. Система из одного ненулевого вектора считается ортогональной.
Опр.5. Ортогональная система векторов, являющаяся базисом евклидового пространства E, называется ортогональным базисом пространства E.
Теорема 1. Любая ортогональная система ненулевых векторов евклидового пространства E линейно независима.
Доказательство: «от противного» Пусть нашлась линейно зависимая ортогональная система ненулевых векторов  . Тогда
. Тогда  , не равные нулю одновременно, такие, что
, не равные нулю одновременно, такие, что  . Пусть, для определенности,
. Пусть, для определенности,  .
.



 Найдем скалярное произведение
Найдем скалярное произведение 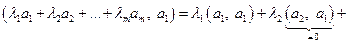

Значит, любая ортогональная система ненулевых векторов линейно независима. ▲.
Теорема 2. В каждом ненулевом конечномерном евклидовом пространстве E существует ортогональный базис.
Доказательство: Пусть E - п-мерное (  ) евклидово пространство, тогда в пространстве E существует базис, состоящий из п векторов. Пусть
) евклидово пространство, тогда в пространстве E существует базис, состоящий из п векторов. Пусть 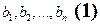 - некоторый базис пространства E. Построим ортогональный базис следующим образом.
- некоторый базис пространства E. Построим ортогональный базис следующим образом.
Положим  .
.
Ищем вектор  в виде
в виде  . Требуем, чтобы
. Требуем, чтобы 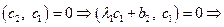
 .
.
Отметим, что  . Действительно, в противном случае имели бы
. Действительно, в противном случае имели бы 
 (1) линейно зависима - противоречие. Итак,
(1) линейно зависима - противоречие. Итак,  .
.
Ищем вектор  в виде
в виде  . Выясним, как надо выбрать коэффициенты
. Выясним, как надо выбрать коэффициенты 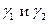 , чтобы
, чтобы 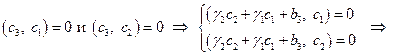

Аналогично предыдущему случаю 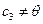 .
.
- - - - - - - - - - - - - - - - -
И, наконец, строим вектор  . Причем
. Причем

Из построения имеем, что  - ортогональная система ненулевых векторов. Тогда по теореме 1 она линейно независима. А любая линейно независимая система, состоящая из п векторов п-мерного пространства, образует его базис. Значит,
- ортогональная система ненулевых векторов. Тогда по теореме 1 она линейно независима. А любая линейно независимая система, состоящая из п векторов п-мерного пространства, образует его базис. Значит,  - ортогональный базис пространства E. ▲.
- ортогональный базис пространства E. ▲.
|
из
5.00
|
Обсуждение в статье: Замена базиса и преобразование координат |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

