 |
Главная |
Базисы в линейном пространстве
|
из
5.00
|
Упорядоченный набор векторов
 (5.5)
(5.5)
линейного пространства  образуют базис в
образуют базис в  , если
, если
1) векторы (5.5) линейно независимы,
2) любой вектор  можно представить в виде линейной комбинации векторов (5.5):
можно представить в виде линейной комбинации векторов (5.5):
 . (5.6)
. (5.6)
Равенство (5.6) называется разложением вектора  по базису (5.5). Для каждого вектора
по базису (5.5). Для каждого вектора  числа
числа  определяются однозначно; они называются координатами вектора
определяются однозначно; они называются координатами вектора 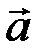 в базисе (5.5).
в базисе (5.5).
При фиксированном базисе соответствие между векторами  и их координатными строками – арифметическими векторами
и их координатными строками – арифметическими векторами  взаимно-однозначно: каждому вектору соответствует единственная строка, разным векторам – разные строки. Как и в случае геометрических векторов, при сложении двух векторов их координатные строки складываются, при умножении на число – умножаются на это число. Вышесказанное позволяет при выполнении линейных операций фактически отождествить вектор
взаимно-однозначно: каждому вектору соответствует единственная строка, разным векторам – разные строки. Как и в случае геометрических векторов, при сложении двух векторов их координатные строки складываются, при умножении на число – умножаются на это число. Вышесказанное позволяет при выполнении линейных операций фактически отождествить вектор  с его координатной строкой и писать
с его координатной строкой и писать  .
.
Линейные пространства, в которых существует базис, называются конечномерными. Можно показать, что любой базис в конечномерном линейном пространстве  содержит одно и то же число векторов. Это число
содержит одно и то же число векторов. Это число  называется размерностью линейного пространства
называется размерностью линейного пространства  ; говорят, что
; говорят, что  –
–  -мерное линейное пространство и обозначают его с указанием размерности:
-мерное линейное пространство и обозначают его с указанием размерности:  .
.
Согласно п. 5.1.5 линейное пространство  геометрических векторов на плоскости двумерно, линейное пространство
геометрических векторов на плоскости двумерно, линейное пространство  геометрических векторов в пространстве трехмерно. Пространство
геометрических векторов в пространстве трехмерно. Пространство 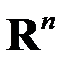
 -мерно.
-мерно.
Линейное пространство, в котором существует любое число линейно независимых векторов и потому не существует базиса, называется бесконечномерным. Например, бесконечномерным является линейное пространство  всех функций на
всех функций на  (см. задачу 5.3.20).
(см. задачу 5.3.20).
Примеры решения задач
5.2.1.
| Рис. 5.4 |

|

|

|

|

|

|
 задан координатами в ортонормированном базисе
задан координатами в ортонормированном базисе  :
:  . Записать разложение
. Записать разложение  по этому базису и изобразить его на рисунке.
по этому базису и изобразить его на рисунке.
◄ Разложение вектора  по базису
по базису  имеет вид
имеет вид  (рис. 5.4). ►
(рис. 5.4). ►
5.2.2.Даны векторы  и
и  . Найти
. Найти  ,
,  ,
,  .
.
◄ Задание можно понимать двояко. 1) В некотором базисе  заданы координаты геометрических векторов
заданы координаты геометрических векторов  и
и  . Надо найти координаты указанных векторов в том же базисе. 2) Заданы арифметические векторы – строки из 3 чисел и надо сделать с ними указанные операции. Наши действия в обоих случаях одинаковы – используем формулы (5.2):
. Надо найти координаты указанных векторов в том же базисе. 2) Заданы арифметические векторы – строки из 3 чисел и надо сделать с ними указанные операции. Наши действия в обоих случаях одинаковы – используем формулы (5.2):
 ,
,  ,
,
 . ►
. ►
5.2.3.Коллинеарны ли векторы  и
и  ,
,  и
и  , если
, если
 ,
,  ,
,  .
.
◄ Координаты векторов 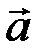 и
и  пропорциональны:
пропорциональны:  . Следовательно,
. Следовательно,  или в более симметричной записи
или в более симметричной записи  , то есть векторы
, то есть векторы 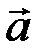 и
и  линейно зависимы и потому коллинеарны:
линейно зависимы и потому коллинеарны:  .
.
Координаты векторов  и
и  не пропорциональны:
не пропорциональны:  . Поэтому векторы
. Поэтому векторы  и
и  не коллинеарны (линейно независимы). ►
не коллинеарны (линейно независимы). ►
5.2.4.Убедиться, что векторы  ,
,  ,
,  линейно зависимы. Найти эту зависимость. Является ли вектор
линейно зависимы. Найти эту зависимость. Является ли вектор  линейной комбинацией векторов
линейной комбинацией векторов  и
и  ?
?
◄ Мы должны показать, что векторы  ,
,  ,
,  удовлетворяют соотношению (5.1):
удовлетворяют соотношению (5.1):  , где хотя бы одно
, где хотя бы одно  отлично от нуля.
отлично от нуля.
Из (5.2) следует, что в координатах это равенство имеет вид

или

Решаем эту систему методом Гаусса.



 ,
, 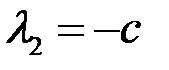 ,
,  , где
, где  .
.
Для определенности возьмем  . Тогда
. Тогда  ,
,  ,
,  . Таким, образом, показано, что векторы
. Таким, образом, показано, что векторы  ,
,  ,
,  линейно зависимы, и эта зависимость имеет вид
линейно зависимы, и эта зависимость имеет вид  . Любой из векторов
. Любой из векторов  ,
,  ,
,  можно представить в виде линейной комбинации остальных векторов. В частности,
можно представить в виде линейной комбинации остальных векторов. В частности,  . ►
. ►
5.2.5.Компланарны ли векторы  ,
,  ,
,  ?
?
◄ Компланарность трех векторов равносильна их линейной зависимости. Поскольку вид линейной зависимости, если она существует, нас не интересует, то удобно не использовать непосредственно определение линейной зависимости, как в задаче 5.2.4, а ограничиться проверкой условия компланарности векторов в форме (5.4):
 ,
,
Следовательно, векторы  ,
,  ,
,  компланарны. ►
компланарны. ►
5.2.6.1) Убедиться, что векторы  ,
,  ,
,  образуют базис; 2) разложить вектор
образуют базис; 2) разложить вектор  по этому базису.
по этому базису.
◄ 1) Так как  , то векторы
, то векторы  линейно независимы (некомпланарны) и образуют базис;
линейно независимы (некомпланарны) и образуют базис;
2) разложение вектора 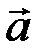 по базису
по базису  имеет вид
имеет вид  . Это векторное равенство в координатной форме равносильно системе линейных уравнений:
. Это векторное равенство в координатной форме равносильно системе линейных уравнений:

Решая эту систему, получаем  ,
,  ,
,  . Значит,
. Значит,  . ►
. ►
5.2.7.Доказать, что множество  всех многочленов от одной переменной степени
всех многочленов от одной переменной степени  с «обычными» операциями сложения и умножения на действительное число является линейным пространством. Найти его базис. Доказать, что множество всех многочленов второй степени, то есть квадратных трехчленов, не является линейным пространством.
с «обычными» операциями сложения и умножения на действительное число является линейным пространством. Найти его базис. Доказать, что множество всех многочленов второй степени, то есть квадратных трехчленов, не является линейным пространством.
◄ 1. Многочлен степени  имеет вид
имеет вид  , где коэффициенты
, где коэффициенты  и
и  – действительные числа. При
– действительные числа. При 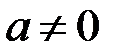
 – многочлен второй степени, при
– многочлен второй степени, при  ,
, 
 – многочлен первой степени, при
– многочлен первой степени, при 
 – многочлен нулевой степени.
– многочлен нулевой степени.
2. Произведение многочлена  на число
на число  – также многочлен
– также многочлен  степени
степени  .
.
Сумма многочленов  и
и  – многочлен
– многочлен  , степень которого не превышает 2. Свойства 1-8 из определения линейного пространства очевидно выполняются. Роль нулевого вектора играет нулевой многочлен
, степень которого не превышает 2. Свойства 1-8 из определения линейного пространства очевидно выполняются. Роль нулевого вектора играет нулевой многочлен  , многочлен, противоположный
, многочлен, противоположный  имеет вид
имеет вид 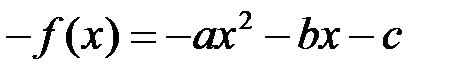 . Таким образом, множество
. Таким образом, множество  всех многочленов степени
всех многочленов степени  с определенными выше операциями суммы и произведения на число является линейным пространством.
с определенными выше операциями суммы и произведения на число является линейным пространством.
3. Покажем, что многочлены  ,
,  ,
,  образуют базис линейного пространства
образуют базис линейного пространства  . Проверим их линейную независимость. Равенство (5.1) в нашем случае имеет вид
. Проверим их линейную независимость. Равенство (5.1) в нашем случае имеет вид  для всех
для всех  , то есть
, то есть  для всех
для всех  . Так как уравнение степени
. Так как уравнение степени  с ненулевыми коэффициентами имеет не более двух корней, то это равенство возможно только при
с ненулевыми коэффициентами имеет не более двух корней, то это равенство возможно только при  . Это означает, что многочлены
. Это означает, что многочлены 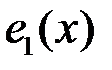 ,
,  ,
,  – линейно независимы. Очевидно, что любой многочлен
– линейно независимы. Очевидно, что любой многочлен  – их линейная комбинация:
– их линейная комбинация:
 .
.
4. Операции над многочленами второй степени могут дать многочлен меньшей степени. Например, произведение числа 0 на многочлен второй степени равно нулю, сумма многочлен второй степени с противоположным многочленом также нуль, а нуль – многочлен нулевой степени. Поэтому множество многочленов второй степени не является линейным пространством. ►
|
из
5.00
|
Обсуждение в статье: Базисы в линейном пространстве |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

