 |
Главная |
К.ф.-м.н., доцент, зав. кафедрой алгебры и геометрии
|
из
5.00
|
Функциональное уравнение - это уравнение, в котором неизвестными являются функции (одна или несколько). Например,
f(x)+xf(x+1) = 1

Некоторые функциональные уравнения знакомы нам еще из школьного курса это f(x) = f(-x), f(-x) = - f(x), f(x+T) = f(x), которые задают такие свойства функций, как чётность, нечётность, периодичность.
Задача решения функциональных уравнений является одной из самых старых в математическом анализе. Они появились почти одновременно с зачатками теории функций. Первый настоящий расцвет этой дисциплины связан с проблемой параллелограмма сил. Ещё в 1769 году Даламбер свёл обоснование закона сложения сил к решению функционального уравнения
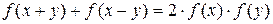 (1)
(1)
То же уравнение и с той же целью было рассмотрено Пуассоном в 1804 году при некотором предположении аналитичности, между тем как в 1821 году Коши (1789 – 1857) нашёл общие решения



этого уравнения, предполагая только непрерывность f(x).
Даже известная формула неевклидовой геометрии для угла параллельности

была получена Н. И. Лобачевским (1792 – 1856) из функционального уравнения
 , (2)
, (2)
которое он решил методом, аналогичным методу Коши. Это уравнение можно привести к уравнению
 .
.
Ряд геометрических задач, приводящих к функциональным уравнениям, рассматривал английский математик Ч. Баббедж (1792—1871). Он изучал, например, периодические кривые второго порядка, определяемые следующим свойством для любой пары точек кривой: если абсцисса второй точки равна ординате первой, то ордината второй точки равна абсциссе первой. Пусть такая кривая является графиком функции у = f(х); (х, f(х)) — произвольная ее точка. Тогда, согласно условию, точка с абсциссой f(х) имеет ординату х. Следовательно,
 (3)
(3)
Функциональному уравнению (3) удовлетворяют, в частности, функции:
 ,
, 
Одними из простейших функциональных уравнений являются уравнения Коши
f(x+y) = f(x)+f(y), (4)
f(x+y) = f(x)·f(y), (5)
f(xy) = f(x)+f(y), (6)
f(xy) = f(x)·f(y), (7)
Эти уравнения Коши подробно изучил в своём (Курсе Анализа), изданном в 1821 году. Непрерывные решения этих четырёх основных уравнений имеют соответственно вид
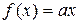 ,
,  ,
,  ,
, 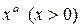
В классе разрывных функций могут быть и другие решения. Уравнение (4) ранее рассматривалось Лежандром и Гауссом при выводе основной теоремы проективной геометрии и при исследовании гауссовского закона распределения вероятностей.
Многие функциональные уравнения не определяют конкретную функцию, а задают широкий класс функций, т. е. выражают свойство, характеризующее тот или иной класс функций. Например, функциональное уравнение f(x+1) = f(x) характеризует класс функций, имеющих период 1, а уравнение f(1+x) = f(1-x) - класс функций, симметричных относительно прямой x = 1, и т. д.
Вообще, для функциональных уравнений, не сводящихся к дифференциальным или интегральным, известно мало общих методов решения. Далее будут рассмотрены некоторые приёмы, позволяющие решать функциональные уравнения.
Для решения функциональных уравнений используются следующие методы:
Ø Метод сведения функционального уравнения к известному уравнению с помощью замены переменной и функции (Метод основан на введении вспомогательной функции, которую следует подобрать таким образом, чтобы после преобразований было ясно, что она удовлетворяет одному из известных функциональных уравнений.)
Ø Метод подстановок (Заменяя некоторые переменные функционального уравнения либо конкретными значениями, либо какими-либо другими выражениями пытаемся либо упростить это уравнение, либо привести его к такому виду, что дальнейшее решение станет очевидным.)
Ø Дифференцирование (В некоторых случаях для нахождения решения функционального уравнения целесообразно продифференцировать обе части уравнения, если, конечно, производная существует. В результате получим функциональное уравнение, которое содержит и производную неизвестной функции. Решим это уравнение относительно производной. Тогда неизвестная функция является одной из первообразных для найденной производной. Этот метод уже применялся при решении уравнения Коши в классе дифференцируемых функций.)
Ø С применением теории групп (Понятие группы позволяет в ряде случаев выбрать целесообразные подстановки для решения функциональных уравнений.) [3]
Ø С применением теории матриц
Под знаком неизвестной функции могут стоять дробно-линейные выражения вида  . Такие дроби полностью определяются заданием матрицы
. Такие дроби полностью определяются заданием матрицы  , составленной из коэффициентов a, b, c, d.
, составленной из коэффициентов a, b, c, d.
Пример. Найти функцию f, определенную при  , удовлетворяющую уравнению
, удовлетворяющую уравнению
 (5.7)
(5.7)
Решение. Решаем матричное уравнение AХ = В, где  ;
;  . Для матрицы A обратной является матрица
. Для матрицы A обратной является матрица  . Тогда
. Тогда  . Матрица X имеет вид
. Матрица X имеет вид  , поэтому применим к уравнению (5.7) подстановку
, поэтому применим к уравнению (5.7) подстановку  . Последнюю удобно выполнять с помощью матриц. Правой части уравнения (5.7) соответствует матрица
. Последнюю удобно выполнять с помощью матриц. Правой части уравнения (5.7) соответствует матрица  . Применение к ней подстановки
. Применение к ней подстановки  равносильно умножению
равносильно умножению  справа на
справа на 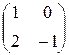 . В результате получим
. В результате получим  . Таким образом, из уравнения (5.7) находим
. Таким образом, из уравнения (5.7) находим
 (5.8)
(5.8)
Исключив из системы, составленной из уравнений (5.7) и (5.8)  имеем
имеем
 (5.9)
(5.9)
Из (5.7) видим, что 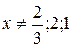 . Подстановка сохранила эти ограничения. Кроме того,
. Подстановка сохранила эти ограничения. Кроме того,  .
.
Положим  . Так как
. Так как  , то
, то  . Отсюда
. Отсюда  . Заменяя
. Заменяя  , из (5.9) получим
, из (5.9) получим
 .
.
Проверка показывает, что эта функция удовлетворяет условию задачи:


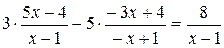
Литература:
1. Андреев А.А., Кузьмин Ю.Н.., Савин А.Н., Саушкин И.Н. Функциональные уравнения. – Самара: В мире науки, 1999
2. Бродский Я.С., Слипенко А.К. Функциональные уравнения. – К.: Вища школа. Головное издательство, 1983.
3. Морозова Е.И. Теоретико-групповой метод решения функциональных уравнений (научный руководитель Троякова Г.А.).- Сборник научных трудов студентов ТывГУ, выпуск VII. Кызыл: изд-во ТывГУ, 2009.
|
из
5.00
|
Обсуждение в статье: К.ф.-м.н., доцент, зав. кафедрой алгебры и геометрии |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

