 |
Главная |
Дифференциальные уравнения с разделяющимися переменными и однородные первого порядка
|
из
5.00
|
Решить дифференциальные уравнения:
800.  . 801.
. 801.  .
.
802.  . 803.
. 803. 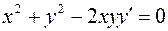 . 804.
. 804.  .
.
805.  . 806.
. 806.  ; y = 0 при x = 1.
; y = 0 при x = 1.
807. Найти линию, проходящую через точку (2; 3) и обладающую тем свойством, что отрезок любой ее касательной, заключенный между координатными осями, делится пополам в точке касания.
808. Найти линию, у которой квадрат длины отрезка, отсекаемого любой касательной от оси ординат, равен произведению координат точки касания.
809. 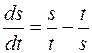 . 810.
. 810. 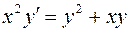 . 811.
. 811. 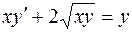 .
.
812.  . 813.
. 813. 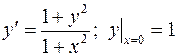 .
.
814. 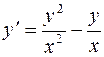 ; y = 1 при х = -1.
; y = 1 при х = -1.
815.  ;
;  при х = 1.
при х = 1.
816. Найти все линии, у которых отрезок касательной между точкой касания и осью абсцисс делится пополам в точке пересечения с осью ординат.
817. Найти линию, у которой длина полярного радиуса любой ее точки M равняется расстоянию между точкой пересечения касательной в точке M с осью OY и началом координат.
Уравнения Бернулли и линейные
Решить дифференциальные уравнения:
818. 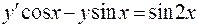 . 819.
. 819.  . 820.
. 820. 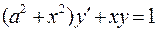 .
.
821.  . 822.
. 822.  . s = 1 при t = –1.
. s = 1 при t = –1.
823.  . y = –1 при x = 1.
. y = –1 при x = 1.
824. Найти линию, у которой начальная ордината любой касательной на две единицы масштаба меньше абсциссы точки касания.
825.  . 826.
. 826.  . 827.
. 827.  .
.
828.  . 829.
. 829.  .
.
830.  ; y = 0,5 при x = 1.
; y = 0,5 при x = 1.
831. Найти уравнение кривой, у которой отрезок, отсекаемый касательной на оси абсцисс, равен квадрату ординаты точки касания.
Уравнения, допускающие понижение порядка
Найти общие решения уравнений:
832.  . 833.
. 833. 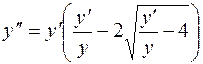 . 834.
. 834.  .
.
835.  . 836.
. 836.  . 837.
. 837.  .
.
838.  . 839.
. 839.  .
.
840.  . 841.
. 841.  .
.
Линейные однородные дифференциальные уравнения с постоянными коэффициентами
Найти общие решения уравнений:
842. у¢¢ + у¢ - 2у = 0. 843. у¢¢ - 4у¢ = 0. 844. у¢¢ + 6у¢ + 13у = 0.
845. y¢¢ - 2y¢ + y = 0. 846. y¢¢¢ + 9y¢ = 0. 847. y(4) = 8y¢¢ - 16y.
848. y¢¢¢ - 13y¢ - 12y = 0. 849. y¢¢ - 9y = 0. 850. y¢¢ - 2y¢ - y = 0.
851. 4y¢¢ - 8y¢ + 5y = 0. 852.  .
.
853. y(4) - 13y¢¢ + 36y = 0. 854. y(4) = 16y. 855. y(4) + 2y¢¢¢ + y¢¢ = 0.
Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами
Найти общие решения уравнений:
856. y¢¢ - 2y¢ + y = e2x. 857. y¢¢ + 3y¢ + 2y = sin 2x + 2cos 2x.
858. y¢¢ + 3y¢ = 9x. 859. y¢¢ + 4y¢ + 5y = 5x2 -32x +5.
860. y¢¢ - 3y¢ + 2y = ex. 861. y¢¢ - 2y = xe-x. 862. y¢¢ - 2y¢ = x2 - x.
863. y¢¢ + 5y¢ + 6y = e-x + e-2x. 864. y¢¢ - 5y¢ + 6y = 13sin 3x.
865. y¢¢ + y¢ + 2,5y = 25cos 2x. 866. y¢¢ - 4y¢ + 4y = 3e2x.
Метод вариации произвольной постоянной
Найти общие решения уравнений:
867. y′′ + y + ctg2x = 0. 868.  . 869.
. 869.  .
.
870. 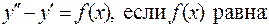 1)
1) 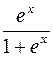 , 2)
, 2)  , 3)
, 3)  .
.
871. 
Глава 6. Ряды
Последовательности
Написать простейшую формулу п-го члена последовательности по указанным членам:
872. 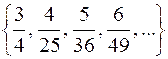 . 873.
. 873.  .
.
По п-му члену последовательности записать ее первые четыре члена и последующий п +1.
874.  . 875.
. 875. 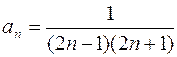 . 876.
. 876.  .
.
877.  . 878.
. 878.  .
.
Найти пределы выражений при неограниченном росте аргумента:
879.  . 880.
. 880.  . 881.
. 881.  .
.
Написать простейшую формулу п-го члена последовательности по указанным членам:
882.  . 883.
. 883.  .
.
По п-му члену последовательности записать ее первые четыре члена и последующий п +1.
884.  . 885.
. 885.  . 886.
. 886. 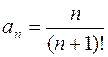 .
.
887. 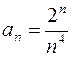 . 888.
. 888. 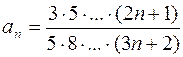 .
.
Найти пределы выражений при неограниченном росте аргумента:
889.  . 890.
. 890.  .
.
891.  .
.
Теоремы сравнения
Исследовать сходимость рядов, применяя признаки сравнения (или необходимый признак):
892.  . 893.
. 893.  . 894.
. 894. 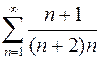 . 895.
. 895. 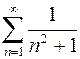 .
.
896. 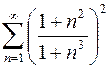 . 897.
. 897.  . 898.
. 898.  . 899.
. 899.  .
.
900. 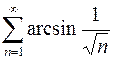 . 901.
. 901.  .
.
902.  . 903.
. 903. 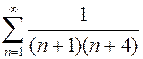 . 904.
. 904.  . 905.
. 905.  .
.
906.  . 907.
. 907.  . 908.
. 908. 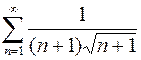 .
.
909.  . 910.
. 910. 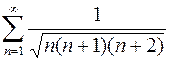 . 911.
. 911.  .
.
Признаки сходимости
Исследовать сходимость знакоположительных рядов:
912.  . 913.
. 913.  .
.
914. 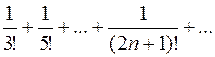 . 915.
. 915.  .
.
916.  . 917.
. 917.  .
.
918. 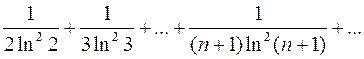 .
.
919.  . 920.
. 920.  .
.
921. 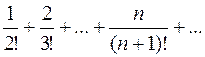 . 922.
. 922.  .
.
923.  . 924.
. 924. 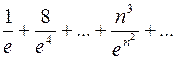 .
.
925.  .
.
|
из
5.00
|
Обсуждение в статье: Дифференциальные уравнения с разделяющимися переменными и однородные первого порядка |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

