Глава 3. Функции нескольких переменных

 

471 . 472.

 

 

473. 474.

475. ; ; .

 

476. ; .

 

477. . . 478. .

 

483. .

 

484. , . 485. , .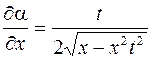

 

486. . 492. . 493. 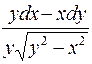. 494. .

 

495. .

 

496. . 497. .

498. .

 

499. . 500. .

 

501. . 502. . 503. . 504. .

 

505. .

 

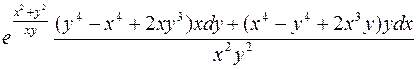506. 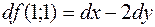; 507. . 508. .

 

509. .

 

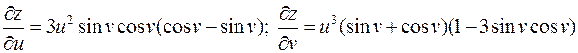510. . 511. . 512. .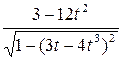

 

513. .

 

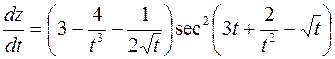514. .

 

515. 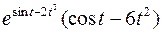. 518. . 519. .

 

520. .

 

521. . 524. . 525. . 527.

 

. 528. .

 

531. 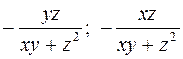. 534. ;

 

 

535. . 538. z_max(4; 4) = 12. 539. z_max(0; 3) = 9.

 

540. z_min(5; 0) = –250, z_max(–5; 0) = 250. 541. .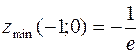

 

542. , . 543. .

 

544. . 545. 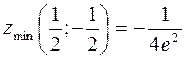. 546. В точке (0; 0) требуются дополнительные исследования. 547. z_min(1; 3) = –2, z_max(–1; 3) = 2. 548. Наибольшее значение z = 17 в тоске (1; 2); наименьшее значение z = –3 в точке (1; 0); стационарная точка (–4; 6) лежит вне заданной области. 549. Наименьшее значение функции z = 0 в точке (0; 0). Наибольшее значение в точках (0; ±1). 550. Наибольшее значение z = 13 в точке (2; 1); наименьшее значение z = –1 в точках (1; 1) и (0; –1). 551. . 552. наибольшие и наименьшие значения лежат на границе области: наибольшее: z = 4 в точках (2; 0) и (–2; 0); наименьшее: z = –4 в точках (0; 2) и (0; –2). Стационарная точка (0; 0) не дает экстремума. 553. Наибольшее значение z = 4 в стационарной точке (2; 1) (эта точка является, таким образом, точкой максимума). Наименьшее значение z = –64 в точке (4; 2) – на границе.

554. . 555.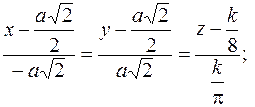

 

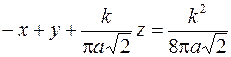. 556. .

 

557. 2x + 4y - z = 3. 558. 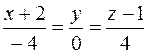. 559. 8x – 8y – z = 4; . 560. 17x + 11y + 5z = 60; .

 

561. .

 

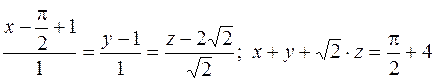562. 27x + 28y + 4z + 2 = 0. 563. z = 0, x + y + z = .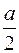

 

564. 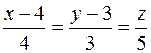. 565. 566. x – y + 2z = ;

 

. 567. . 568. grad z = .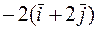

 

569. {–2; 1}. 570. . 571. |grad z| = . 572. 1 в направлении оси Oy. 573. φ = π. 574. φ = 8˚. 575. 0. 576. .

 

577. 0,25. 578. –2. 579. . 580. . 581. 3 в направлении вектора 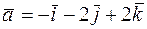. 582. 0. 583. 0. 584. . 585. –0,4. 586. .

 

587. 0,25. 588. .

 

Глава 4. Интегрирование функций

 

589. . 590. .

 

591. ; 592. . 593. .

 

594. 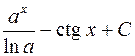. 595. . 596. .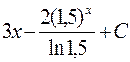

 

597. . 598. . 599. .

 

600. . 601. . 602. .

 

603. . 604. . 605. 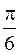. 606. .

 

607. . 608. .

 

609. . 610. . 611. .

 

612. . 613. . 614. . 615. .

 

616. 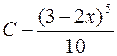. 617. . 618. .

 

619. . 620. .

 

621. . 622. . 623. 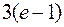. 624. .

 

625. . 626. 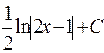. 627. .

 

628. 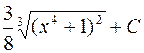. 629. . 630. . 631. .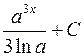

632. . 633. . 634. . 635. .

 

636. . 637. . 638. .

 

639. . 640. .

 

641. . 642. 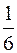. 643. . 644. .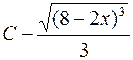

 

645. . 646. . 647. . 648. .

 

649. . 650. 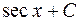. 651. .

 

652. . 653. . 654. .

 

655. . 656. .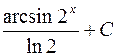

 

657. . 658. .

 

659. . 660. . 661. .

 

662. . 663. .

 

664. . 665. . 666. 2ln 2-1.

 

667. . 668. .

 

669. .

 

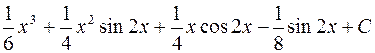670. . 671. .

 

672. . 673. .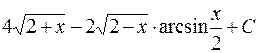

 

674. 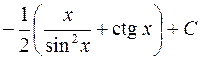. 675. . 676. .

 

677. 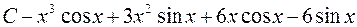. 678. .

 

679. . 680. .

 

681. 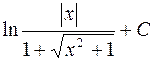. 682. . 683. .

 

684. . 685. . 686. .

 

687. 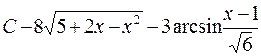. 688. 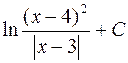. 689. . 690. 1.

 

691. . 692. .

 

693. . 694. . 695. .

 

696. . 697. . 698.

 

.

 

699. . 700. .

701. . 702. .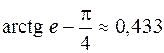

703. 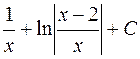. 704. . 705. .

 

706. . 707. .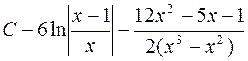

 

708. 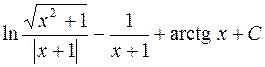. 709. .

 

710. . 711. .

 

712. . 713. .

 

714. . 715. .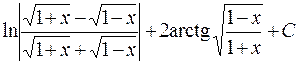

 

716. . 717. .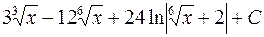

 

718. . 719. .

 

720. .

 

721. .

 

722. .

 

723. . 724. .

725. .

 

726. .

 

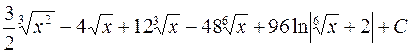727. .

 

728. .

 

729. .

 

730. .

 

731. . 732. .

733. . 734. . 735. .

 

736. . 737. . 738. .

 

739. 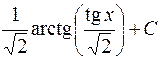. 740. . 741. .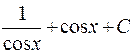

 

742. . 743. . 744. .

 

745. . 746. . 747. . 748. .

 

749. . 750. . 751. .

 

752. ≈9,2. 753. . 754. . 755. .

 

756. 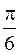. 757. . 758. . 759. 1. 760. 0,5. 761. ln 2. 762. 2.

 

763. . 764. 1. 765. π. 766. Расходится. 767. . 768. .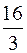

 

769. 3pа². 770. 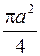. 771. . 772. . 773. .

 

774. . 775. 18pа². 776.

 

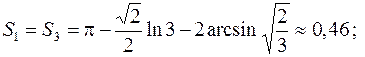
. 777. . 778. 6а. 779. 8a. 780. . 781. .

 

782. . 783. ln3 – 0,5. 784. . 785. . 786. .

787. 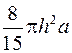. 788. . 789. . 790. .

 

791. 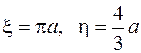. 792. .

 

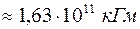793. . 794. а) 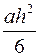. б) в два раза.

 

795. . 796. 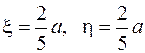. 797. 353 250 кГм.

 

798. 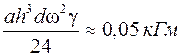. 799. 22,2 т.

 

Глава 5. Дифференциальные уравнения

 

800. 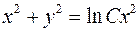. 802. ln y = tg . 802. .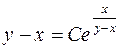

 

803. . 804. 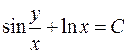. 805. . 806. .

 

807. Гипербола xy = 6. 808. 809. .

 

810. . 811. При х > 0 , при x < 0 .

 

812. . 813. . 814. , .

 

815. , 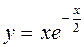. 816. Параболы y² = Cx. 817. x² = 2Cy + C².

 

818. . 819. . 820. .

 

821. . 822. , .

 

823. , 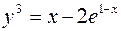. 824. .

 

825. . 826. . 827. .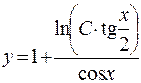

 

828. . 829. .

 

830. . 831. x = y² + Cy. 832. .

 

833. . 834. .

 

835. . 836. .

 

837. 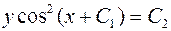. 838. , C₁ > 0.

 

839. , если С₁ < 0, и

 

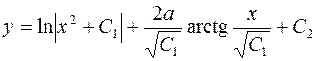, если С₁ > 0.

 

840. . 841. .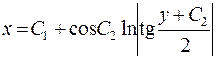

 

842. у = С₁е^х + С₂е^-2х. 843. у = С₁е^4х + С₂.

 

844. у = е^-3х(С₁cos 2x + C₂sin 2x). 845. y = (C₁ + C₂x)e^x.

 

846. y = C₁cos 3x + C₂sin 3x + C₃. 847. y = (C₁ + C₂x)e^2x + (C₃ + C₄x)e^-2x.

 

848. y = C₁e^-x + C₂e^-3x + C₃e^4x. 849. y = C₁e^3x + C₂e^-3x.

 

850. . 851. .

 

852. . 853. y = C₁e^2x + C₂e^-2x + C₃e^3x + C₄e^-3x.

 

854. y = C₁e^2x + C₂e^-2x + C₃cos 2x + C₄sin 2x.

 

855. y = C₁ + C₂x + C₃e^-x + C₄xe^-x. 856. y = (C₁ + C₂x)e^x + e^2x.

 

857. . 858. y = C₁ + C₂e^-3x + 1,5x² - x.

 

859. y = e^-2x(C₁cos x + C₂sin x) + x² -8x +7. 860. y = C₁e^2x + (C₂ - x)e^x.

 

861. . 862. .

 

863. y = C₁e^-2x + C₂e^-3x + 0,5e^-x + xe^-2x.

 

864.

 

865. .

 

866. y = e^2x(C₁ + C₂x + 1,5x²).

 

867. .

 

868. .

 

869. .

 

870. 1) ,

 

2) ,

 

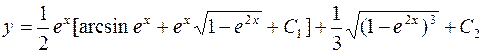3) .

 

871. .

 

Глава 6. Ряды

 

872. . 873. .

 

874. .

 

875. .

 

876. . 877. .

 

878. .

 

879. 0; 880. 0; 881. 0. 882. . 883. .

 

884. .

 

885. .

 

886. ; 887. .

 

888. .

 

889. 0. 890. 0. 891. 0. 892. Сходится. 893. Расходится.

894. Расходится. 895. Сходится. 896. Сходится. 897. Сходится.

898. Сходится. 899. Расходится. 900. Расходится. 901. Расходится.

902. сходится. 903. сходится. 904. Расходится. 905. Расходится.

906. сходится. 907. Расходится. 908. сходится. 909. Расходится.

910. сходится. 911. Расходится. 912.сходится. 913. сходится.

914. сходится. 915. сходится. 916. сходится. 917. сходится.

918. сходится. 919. сходится. 920. сходится. 921. сходится.

922. сходится. 923. сходится. 924. сходится. 925. сходится.

926. сходится условно. 927. сходится абсолютно. 928. Расходится.

929. сходится абсолютно. 930. сходится условно. 931. сходится абсолютно. 932. сходится абсолютно. 933. Расходится.

934. Расходится. 935. сходится условно. 936. сходится абсолютно.

937. Расходится. 938. сходится условно. 939. сходится абсолютно.

940. (–1; 1]. 941. (–0,1; 0,1). 942. . 943. (–4; 4). 944. (–2; 2).

945. (2; 8]. 946. [0; 4). 947. (1; 3]. 948. (2; 4]. 949. [–1; 1). 950. (–2; 2).

951. [–10; 10). 952. [–2; 2). 953. [–3; 3). 954. [–2; 8). 955. [–4; –2].

956. (–1,25; 3,25). 957. [1; 5).

 

958. .

 

959. . 960. .

 

961. . 962. .

 

963. .

 

964. .

 

965. . 966. .

 

967. .

 

968. .

 

969. .

 

970. 4,121. 971. 32,831. 972. .

 

973. 3,107. 974. 0,487. 975. .

 

976. . 977. .

 

978. . 979. .

 

980. 1) ; 2) .

 

981. .

 

982. . 983. .

 

984. .

 

985.

 

 

. 986. .

 

987. а) ; б) .

 

988. а) ; б) .

 

989. а) ; б) .

 

Глава 7. Кратные интегралы

 

990. . 991. . 992. . 993. ;

 

994. . 995. 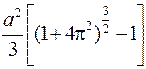. 996. δa. 997. .

 

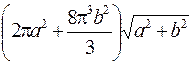998. 3. 999. . 1000. 1) , 2) , 3) , 4) . 10001. 0.

 

1002. . 1003. . 1004. 4π. 1005. Во всех четырех случаях интеграл равен 1.

 

1006. –2πab. 1007. . 1008. 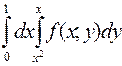. 1009. .

 

1010. . 1011. . 1012. . 1013. .

 

1014. .

 

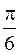1015. . 1016. . 1017. πR ²h. 1018. . 1019. .

 

1020. 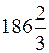. 1021. 16. 1022. 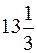. 1023. . 1024. .

1025. . 1026. 45. 1027. .

 

1028. . 1029. . 1030. .

 

1031. . 1032. .

 

1033. . 1034. . 1035. . 1036. . 1037.

 

Перейти к цилиндрическим координатам. 1038. 8π.

 

1039. . 1040. . 1041. . 1042. .

 

1043. 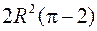. 1044. . 1045. . 1046. 8.

 

1047. . 1048. 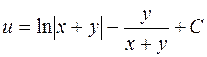. 1049. .

 

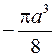1050. . 1051. 1) 0, 2) . 1052. 4.

 

1053. . 1054. . 1055. 6πa².

 

1056. . 1057. . 1058. . 1059. . 1060. 0. 1061. .

 

Список рекомендуемой литературы

 

Берман, Г. Н. Сборник задач по курсу математического анализа. – 19 изд. – М: Наука. Гл. ред. физ