Чувствительность и устойчивость

При реализации управленческого решения зачастую имеют место возмущения по каким-либо параметрам системы, обусловленные внешними и внутренними факторами. Эти возмущения приводят к изменению оптимальных значений переменных задачи (объема производства продукции) и целевой функции (прибыли). Поэтому, возникает задача об оценке их влияния на управленческое решение и на базе нее формулировки конкретных действий, которые нужно предпринять в этих условиях.

Для решения поставленной задачи используем математический аппарат теории чувствительности. Пусть существует следующая задача линейного программирования:

Ф= С_iX_j →max α_ij X_j ≤ b_i

Найдено оптимальное решение задачи, то есть определены выходные характеристики задачи, а именно оптимальные значения переменных х° и целевой функции Ф°. Продукцию, для которой х_i°>0 , будем называть «выгодной»; продукцию, для которой х_i° = 0 - «невыгодной». Введем характеристику запасов ресурсов у_i=b_i- а_ijх_j°, которая показывает количество ресурса i-ro вида, оставшегося после реализации оптимального решения.

Если у_i =0, то ресурс будем называть «дефицитным». Если у_i>0 – ресурс «недефицитный».

Оценим влияние изменения запасов i-ого ресурса на выходные характеристики задачи. Для этого введем в рассмотрение коэффициенты чувствительности , которые показывают, на сколько изменится значение j-ой переменной при увеличении запаса i-го ресурса на единицу. Данные коэффициенты отличны от нуля для «дефицитных» ресурсов и равны нулю для «недефицитных».

Коэффициенты чувствительности показывают на сколько изменится значение целевой функции при увеличении запаса i-го ресурса на единицу.

Найдем коэффициенты чувствительности для функции определения оптимальной производственной программы. Пусть целевой функцией является максимизация прибыли, а ограничениями выступают запасы сырьевых ресурсов.

Ф=5.52Х₁+3,62Х₂→max

2X₁+3X₂≤1000 |b₁

X₁ ≤ 446,73 |b₂

X₂ ≤ 295,4 |b₃

Оптимальным решением задачи является х₁°= 446,73, х₂°=35,51. Так как х₁°, х₂°>0, следовательно, и первая, и вторая продукция «выгодные». Определим резервы по ресурсам: у₁ =0, у₂=0, у₃=259,89. Отсюда делаем вывод, что первый и второй ресурс являются «дефицитными», третий - «недефицитным». Так как коэффициенты чувствительности для «недефицитного» ресурса равны нулю, следовательно

Для определения оставшихся коэффициентов, исключаем из системы ограничений третье неравенство, в двух других переходим к строгим равенствам и, обозначив правые части через b₁ и b₂, получим следующую систему уравнений:

2X₁+3X₂ = b₁

X₁ = b₂

Продифференцируем данную систему по b₁:

С учетом, что , имеем:

Отсюда . Аналогично после дифференцирования по b₃ определим , .

Рассчитаем коэффициенты чувствительности целевой функции к вариациям «дефицитных» ресурсов:

z₁=c₁α₁¹+c₂α₂¹=5,52*0+3,62*1/3=1,2

z₂=c₁α₁²+c₂α₂²=5,52*1+3,62*(-2/3)=3,11

Под устойчивостью управленческих решений в задачах оптимизации обычно понимают неизменность опорного базиса системы. В данной задаче нахождения оптимального плана выпуска продукции опорный базис - ситуация, при которой сохраняется номенклатура выгодной и невыгодной продукции, а также номенклатура дефицитных и недефицитных ресурсов.

Исследуем опорный базис системы. Предположим, что возникли возмущения по некоторому дефицитному ресурсу ∆b_S. Это изменение приведет к изменению значений переменных x_j, а именно .

Если известно оптимальное значение переменной х_j°, то новое значение переменной определяется как:

Условием неизменности базиса является тот факт, что объем продукции j должен быть положительным . Если он станет равным нулю, следовательно, продукция не будет включена в производственную программу, то есть она из разряда «выгодных» перейдет в «невыгодные», Математически это условие запишется как:

или

Это выражение позволяет сделать аналитическую оценку величины изменения ∆b_s, которое не приводит к смене опорного базиса системы.

Рассмотрим возможный диапазон колебания дефицитного ресурса ∆b_s. Если а_j^s > 0, то добавление ресурса s приведет к увеличению объема выпуска j –той продукции, следовательно, в этом случае изменение опорного базиса системы не произойдет. Если a_j^s < 0, то добавление ресурса s может привести к изменению опорного базиса, то есть объем выпуска j -той продукции может стать равным нулю, то есть продукция не будет выпускаться.

Рассмотрим недефицитный ресурс b_i, для него резерв у_i ≠0и рассчитывается как Предположим, возникло возмущение по запасу дефицитного ресурса ∆b_s, оно приведет к изменению значений переменных ∆х_j. В свою очередь, изменение ∆х_j приведет к изменению запасов недефицитных ресурсов ∆у_j (∆b_s →∆x_j →∆у_j). Следовательно, может возникнуть такая ситуация, когда ∆b_s приведет к тому, что запас недефицитного ресурса станет равным нулю (∆у_j=0). Это означает, что недефицитный ресурс стал дефицитным, то есть изменилась номенклатура ресурсов и произошла смена опорного базиса системы. В этом случае математическая формулировка условия неизменности базиса имеет вид:

Для нашей задачи устойчивость опорного базиса рассчитывается следующим образом.

Ф=5,52Х₁+3,62Х₂→max

2X₁+3X₂≤1000 |b₁

X₁ ≤ 446,73|b₂

X₂ ≤ 295,4 |b₃

Оптимальным решением задачи является х₁°= 446,73, х₂°=35,51. Резервы по ресурсам: у₁ =0, у₂=0, у₃=259,89. Отсюда делаем вывод, что первый и второй ресурс являются «дефицитными», третий - «недефицитным». Отсюда исходный опорный базис системы представляет собой две «выгодные» продукции, 1-ый и 2-ий дефицитные и 3-й недефицитный ресурсы.

Определим диапазон изменения запасов дефицитных ресурсов b1 и b2, в рамках которого смена опорного базиса не произойдет:

Δb_1,1=-x₁⁰/α₁¹=∞

Δb_1,2= -x₂⁰/α₂¹=-106,53

Следовательно, если фонд времени уменьшится на 107 единиц, произойдет смена опорного базиса системы (график 8). Вторая продукция станет невыгодной, откажемся от её производства.

Аналогично для третьего ресурса:

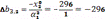
Δb_2,1=-x₁⁰/α₁²=-446,73

Δb_2,2= -x₂⁰/α₂²=53,26

Следовательно, если спрос уменьшится на 447 единиц, то выпускать первую продукцию станет невыгодно, откажемся от её производства. Если спрос на первую продукцию возрастёт на 54 единицы, то производить вторую продукцию станет невыгодно. При увеличении запаса третьего (недефицитного) ресурса смены опорного базиса не произойдет, а при уменьшении на некоторую величину b₃, возникает ситуация, когда ресурс становится дефицитным. Из выражения следует, что

Δ b₃=y₃=-259,89