 |
Главная |
Уравнение Клапейрона – Клаузиуса. Зависимость давления насыщенного пара жидкости от температуры
|
из
5.00
|
При увеличении температуры возрастет доля быстрых молекул, способных преодолеть силы межмолекулярного притяжения и оторваться от поверхности жидкости. Вследствие этого возрастает скорость испарения жидкости и динамическое равновесие жидкости и пара устанавливается при новом более высоком давлении пара. Количественную зависимость давления насыщенного пара от температуры можно получить из уравнения Клапейрона – Клаузиуса, которое в данном случае запишется в виде: 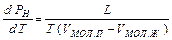 (IX.7).
(IX.7).
Пренебрегая в (X.7) объёмом жидкости и выражая объём пара из уравнения состояния идеального газа РН VМОЛ. П = RT, получим:
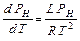 (IX.8).
(IX.8).
Полученное уравнение лежит в основе одного из распространенных методов измерения теплоты испарения, которое и используется в данной работе. Для определения молярной теплоты испарения жидкости удобно вначале построить график зависимости экспериментально измеренного давления насыщенного пара от температуры в специальных линеаризующих координатах ln РН = f (1/T).
В этих координатах график будет близок по форме к прямой линии. Угловой коэффициент этого графика в произвольной точке в соответствии с (IХ.8)
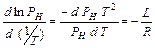 (IX.9).
(IX.9).
Чтобы найти зависимость давления насыщенного пара жидкости от температуры в явном виде можно проинтегрировать уравнение (IX.8) в пределах от некоторого начального состояния Т0, РН0 до произвольного Т, РН (Т).
 (IX.10)
(IX.10)
В полученном уравнении (X.10) остается неизвестной зависимость L температуры Т. В простейшем случае, считая L = const можно получить:

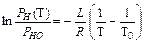
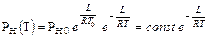
В общем случае молярная теплота испарения L зависит от температуры. При увеличении температуры она обычно уменьшается и при критической температуре становится равной нулю. Чтобы найти зависимость L от Т вначале найдём изменение внутренней энергии 1 моля вещества при переходе из состояния жидкости при температуре Т0 и давлении РНАС. 0, равном давлению насыщающих паров жидкости при этой температуре, в состояние насыщенного пара при температуре Т и давлении РНАС. Поскольку внутренняя энергия зависит только от состояния вещества в данный момент, изменение внутренней энергии ∆U будет одинаково для любых процессов между данными начальным и конечным состояниями.
 Рассмотрим два случая (рис 18)
Рассмотрим два случая (рис 18)
Рис. 18 К выводу зависимости L(T) при Т > Т0 РН > РН0
В первом случае процесс идет по пути a-b-c-d. В процессе а-b температура жидкости постоянна, изменение объема жидкости благодаря малой сжимаемости жидкости незначительно и изменение внутренней энергии так же незначительно ∆Uab ≈ 0. В процессе b-с объём жидкости так же меняется незначительно и вся подводимая для нагрева теплота идет на изменение внутренней энергии. Считая молярную теплоемкость СЖ жидкости постоянной, найдем ∆Ubс = СЖ (Т - Т0). В процессе c-d для испарения жидкости при температуре Т и давлении Рн требуется теплота L, из которой часть Lr = RТ идет на работу расширения, ставшаяся часть L – RТ = Li = Uмол. исп идет на увеличение внутренней энергии вещества при испарении. Результирующее изменение внутренней энергии
∆Uad = ∆Uab + ∆Ubc + ∆Ucd = СЖ (Т-Т0) + L0 – RT.
Во – втором случае процесс идет по пути a-e-d. В процессе а-е аналогично процессу c-d ∆Uае = L0 – RT, где L0 – молярная теплота испарения жидкости при температуре Т0 и давлении РНАС. О.
В процессе e-d изменяется только состояние пара. Считая пар идеальным газом, у которого внутренняя энергия зависит только от температуры, можно записать ∆Ued = СV (Т-Т0), где CV – молярная теплоемкость пара при постоянном объеме. Результирующее изменение внутренней энергии
∆Uad = ∆Uae + ∆Ued = L0 – RT + СV (Т-Т0).
Приравнивая ∆Uad для обоих случаев, получим:
L = L(T) = L0 + (R + CV – CЖ)(T – T0) = L0 + (CP – CЖ)(T – T0) (IX.11).
Поскольку теплоемкость жидкости СЖ больше теплоемкости пара СР при увеличении температуры Т молярная теплота испарения жидкости L уменьшается.
Подставив (IX.11) в (IX.10) можно получить более точную зависимость L от Т (см. [1. стр. 236])
3. Зависимость давления насыщенного пара жидкости от кривизны поверхности.
Если поверхность жидкости не плоская, то сила притяжения, возвращающая вылетающую молекулу обратно в жидкость, зависит от радиуса этой поверхности (рис. 19)
 Рис.19 Зависимость силы притяжения молекул к жидкости от радиуса кривизны поверхности жидкости.
Рис.19 Зависимость силы притяжения молекул к жидкости от радиуса кривизны поверхности жидкости.
При выпуклой поверхности жидкости, вылетающие из жидкости молекулы, удерживаются силами притяжения к меньшему числу молекул, чем в случае плоской поверхности. Поэтому при одинаковой температуре число молекул, вылетающих через выпуклую поверхность жидкости больше, чем число молекул, вылетающих через плоскую поверхность, и динамическое равновесие между жидкостью и паром в случае выпуклой поверхности установится при большем давлении насыщенного пара. В случае вогнутой поверхности, наоборот, давление насыщенного пара уменьшится по сравнению с плоской поверхностью.
Количественную зависимость давления насыщенного пара от радиуса кривизны поверхности жидкости, с которой пар находиться в динамическом равновесии, дает уравнение
PН(Т, r) = PН(T) +  (IX.12)
(IX.12)
где РН (Т) – давление насыщенного пара над плоской поверхностью жидкости (r = ∞), σ – коэффициент поверхностного натяжения на границе с паром,ρП – плотность насыщенного пара, ρЖ – плотность жидкости, r – радиус кривизны. Для выпуклой поверхности жидкости r > 0, для вогнутой r < 0. Уравнение (IX.12) применимо при не слишком малых r, пока второе слагаемое в (X.12) остаётся значительно меньше первого.
|
из
5.00
|
Обсуждение в статье: Уравнение Клапейрона – Клаузиуса. Зависимость давления насыщенного пара жидкости от температуры |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

