 |
Главная |
СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
|
из
5.00
|
Положение точки в пространстве в декартовой системе координат определяется тремя координатами:  . Можно выбрать другие три параметра
. Можно выбрать другие три параметра  и назвать их криволинейными или обобщенными координатами точки. Декартовы координаты будут зависеть от криволинейных:
и назвать их криволинейными или обобщенными координатами точки. Декартовы координаты будут зависеть от криволинейных:
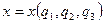 ,
,  ,
,  .
.
Движение точки в криволинейных координатах задается уравнениями
 ,
,  ,
,  .
.
Радиус-вектор 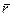 движущейся точки, начало которого находится в неподвижной точке выбранной системы отсчета для рассматриваемого движения, является функцией как декартовых, так и криволинейных координат, т.е.
движущейся точки, начало которого находится в неподвижной точке выбранной системы отсчета для рассматриваемого движения, является функцией как декартовых, так и криволинейных координат, т.е.
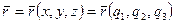 .
.
Выберем точку 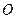 , в которой криволинейные координаты равны нулю, и рассмотрим зависимость
, в которой криволинейные координаты равны нулю, и рассмотрим зависимость  . Получим уравнение в векторной форме координатной линии для
. Получим уравнение в векторной форме координатной линии для  , проходящей через точку
, проходящей через точку 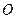 . Аналогично получаются уравнения координатных линий
. Аналогично получаются уравнения координатных линий 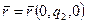 и
и  , проходящих через точку
, проходящих через точку 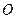 для координат
для координат 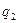 и
и  .
.
Через каждую точку пространства можно провести три координатные линии, пересекающиеся в этой точке. Вдоль каждой из координатных линий изменяется только одна криволинейная координата, а две другие сохраняют постоянные значения, соответствующие рассматриваемой точке.
Рассмотрим частные производные  . Они как производные от вектора по скалярному аргументу направлены по касательным к координатным линиям, являющимся годографами радиуса-вектора. Введем единичные векторы, направленные по векторам
. Они как производные от вектора по скалярному аргументу направлены по касательным к координатным линиям, являющимся годографами радиуса-вектора. Введем единичные векторы, направленные по векторам  . Эти три единичных вектора
. Эти три единичных вектора  называются базисными векторами. Базисные векторы, как и
называются базисными векторами. Базисные векторы, как и  , направлены в каждой точке по касательным к координатным линиям в сторону возрастания криволинейных координат. Направления возрастания и начало отсчета криволинейных координат выбираются при задании движения.
, направлены в каждой точке по касательным к координатным линиям в сторону возрастания криволинейных координат. Направления возрастания и начало отсчета криволинейных координат выбираются при задании движения.
В общем случае базисные векторы могут быть неортогональными. Используя базисные векторы, получаем
 , или
, или 
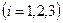 . (36)
. (36)
Скалярные величины  называются коэффициентами Ламэ.
называются коэффициентами Ламэ.
Для вычисления  , учтем, что радиус-вектор через декартовы координаты можно выразить в форме
, учтем, что радиус-вектор через декартовы координаты можно выразить в форме
 (37)
(37)
где  – единичные векторы, направленные по осям декартовой системы координат. Из (37) имеем:
– единичные векторы, направленные по осям декартовой системы координат. Из (37) имеем:
 ,
,
и, следовательно:
 . (38)
. (38)
Скорость точки в криволинейных координатах
При движении точки ее радиус-вектор через обобщенные координаты зависит от времени, т.е.
 .
.
По определению скорости и правилу дифференцирования сложных функций имеем
 , (39)
, (39)
где  называется обобщенной скоростью точки. Используя (36), из (39) получаем
называется обобщенной скоростью точки. Используя (36), из (39) получаем
 . (40)
. (40)
Получено разложение скорости по осям, направление которых совпадает с направлением базисных векторов.
Для величин составляющих скорости по базисным векторам из (40) имеем

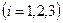 . (40')
. (40')
В случае ортогональности базисных векторов по формуле (40') вычисляются проекции вектора скорости на оси, направленные по базисным векторам. В этом случае для квадрата скорости получаем
 .
.
|
из
5.00
|
Обсуждение в статье: СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

