 |
Главная |
Производная и дифференциал
|
из
5.00
|
Определение 1. Пусть функция 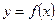 определена на множестве
определена на множестве 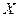 , точки
, точки  и
и 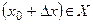 . Производной функции
. Производной функции 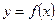 в точке
в точке 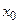 называется предел отношения приращения функции в этой точке к приращению аргумента при
называется предел отношения приращения функции в этой точке к приращению аргумента при 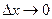 (при условии, что этот предел существует):
(при условии, что этот предел существует): 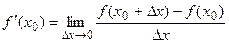 .
.
Определение 2.Функция 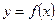 называется дифференцируемой в точке
называется дифференцируемой в точке 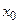 , если её приращение в этой точке можно представить в виде
, если её приращение в этой точке можно представить в виде  , где
, где 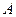 – вещественное число,
– вещественное число, 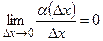 .
.
Теорема 1.Для того чтобы функция 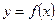 являлась дифференцируемой в точке
являлась дифференцируемой в точке 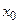 , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы 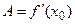 .
.
Определение 3. Дифференциалом 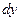 функции
функции 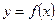 в точке
в точке 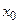 называется главная линейная относительно
называется главная линейная относительно 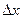 часть приращения функции в этой точке:
часть приращения функции в этой точке: 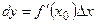 .
.
Определение 4. Дифференциалом 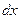 независимой переменной называется приращение
независимой переменной называется приращение 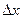 этой переменной:
этой переменной:  .
.
Основные правила вычисления производных
1. Если функции 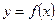 ,
, 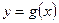 дифференцируемы в точке
дифференцируемы в точке 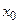 , то сумма (разность), произведение и частное (при условии
, то сумма (разность), произведение и частное (при условии 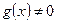 ) этих функций также дифференцируемы в точке
) этих функций также дифференцируемы в точке 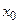 , причем справедливы следующие формулы:
, причем справедливы следующие формулы:
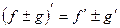 ,
, 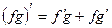 ,
, 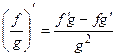 .
.
2. Если функция 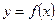 дифференцируема в точке, а
дифференцируема в точке, а  – число, то
– число, то  .
.
3. Пусть функция 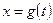 имеет производную в точке
имеет производную в точке 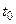 , а функция
, а функция 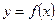 имеет производную в точке
имеет производную в точке 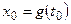 . Тогда сложная функция
. Тогда сложная функция 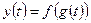 имеет производную в точке
имеет производную в точке 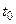 и справедлива формула:
и справедлива формула: 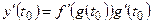 .
.
4. Если функция  определена, непрерывна и строго монотонна на отрезке
определена, непрерывна и строго монотонна на отрезке 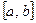 , то у нее существует обратная функция
, то у нее существует обратная функция 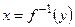 , производная которой вычисляется по формуле:
, производная которой вычисляется по формуле: 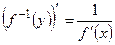 .
.
Таблица производных элементарных функций
1. 
| 2. 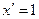
| 3. 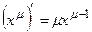 , , 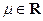
|
4. 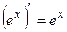
| 5. 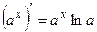 , , 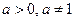
| 6. 
|
7.  , , 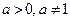
| 8. 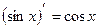
| 9. 
|
10. 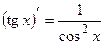
| 11. 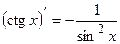
| 12. 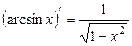
|
13. 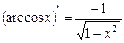
| 14. 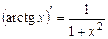
| 15. 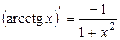
|
Основные правила вычисления дифференциалов
1. Если функции 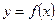 ,
, 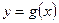 дифференцируемы в точке
дифференцируемы в точке 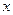 , принадлежащей их общей области определения, то сумма (разность), произведение и частное (при условии
, принадлежащей их общей области определения, то сумма (разность), произведение и частное (при условии 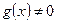 ) этих функций также дифференцируемы в этой точке, причем справедливы следующие формулы:
) этих функций также дифференцируемы в этой точке, причем справедливы следующие формулы:
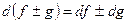 ,
, 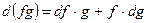 ,
, 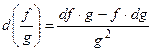 .
.
2. Если функция 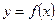 дифференцируема в точке
дифференцируема в точке 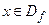 , а
, а 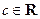 , то
, то  .
.
3. Пусть функция 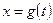 дифференцируема в точке
дифференцируема в точке 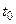 , а функция
, а функция 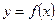 дифференцируема в точке
дифференцируема в точке 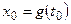 . Тогда сложная функция
. Тогда сложная функция 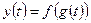 дифференцируема в точке
дифференцируема в точке 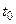 и справедлива формула:
и справедлива формула: 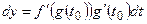 .
.
Таблица дифференциалов элементарных функций
1. 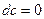
| 2. 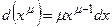 , , 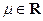
| 3. 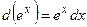
|
4. 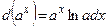 , , 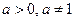
| 5. 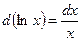
| 6. 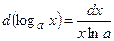 , , 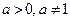
|
7. 
| 8. 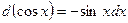
| 9. 
|
10. 
| 11. 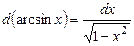
| 12. 
|
13. 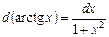
| 14. 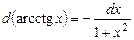
|
Пример 1.Вычислить производную функции  .
.
Решение.  .
.
Пример 2.Найти первый дифференциал функции 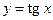 в точке
в точке  .
.
Решение. 1) Вычислим производную функции 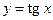 :
: 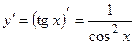 .
.
2) Вычислим значение производной функции 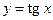 в точке
в точке  :
: 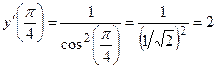 .
.
3) Тогда  .
.
Уравнение касательной к графику функции 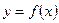 в точке
в точке 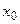 :
:
 .
.
Геометрический смысл производной: значение производной функции 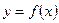 в точке
в точке 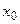 равно тангенсу угла наклона к положительному направлению оси
равно тангенсу угла наклона к положительному направлению оси 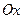 касательной к графику этой функции в точке
касательной к графику этой функции в точке 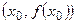 .
.
Пример 3. Составить уравнение касательной к графику функции 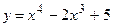 в точке
в точке 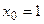 .
.
Решение. 1) Вычислим 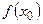 при
при 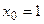 :
:  .
.
2) Вычислим значение производной функции 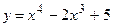 в точке
в точке 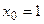 :
: 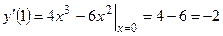 .
.
3) Составим уравнение касательной:  или
или 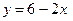 .
.
Экономический смысл производной: производная объёма произведенной продукции по времени 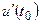 есть производительность труда в момент
есть производительность труда в момент 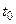 .
.
|
из
5.00
|
Обсуждение в статье: Производная и дифференциал |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

