 |
Главная |
РЕШЕНИЕ ЗАДАЧ ТИПА 41–60
|
из
5.00
|
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ КОНТРОЛЬНОЙ
РАБОТЫ
РЕШЕНИЕ ЗАДАЧИ ТИПА 1–20
Задача. Вычислить определитель  1) разложением по первой строке; 2) по правилу треугольника; 3) с использованием элементарных преобразований.
1) разложением по первой строке; 2) по правилу треугольника; 3) с использованием элементарных преобразований.
Решение. 1) Воспользуемся формулой
 .
.
В нашем случае

 .
.
2) Правило треугольника имеет вид 
 .
.
Применяя это правило для вычисления заданного определителя, получаем
 .
.
3) Получим с помощью тождественных преобразований из исходного определителя новый, который содержит два нулевых элемента, например, в первом столбце. Для этого сначала умножим первую строку заданного определителя на  и результат прибавим ко второй строке определителя. Затем умножим первую строку исходного определителя на
и результат прибавим ко второй строке определителя. Затем умножим первую строку исходного определителя на  и результат прибавим к третьей его строке. В результате получим следующий определитель, равный данному:
и результат прибавим к третьей его строке. В результате получим следующий определитель, равный данному:  . Теперь находим значение полученного (а значит, и исходного) определителя с помощью его разложения по элементам первого столбца:
. Теперь находим значение полученного (а значит, и исходного) определителя с помощью его разложения по элементам первого столбца:
 =
= 
 .
.
РЕШЕНИЕ ЗАДАЧИ ТИПА 21–40
Задача.Пусть ,
,  ,
,  .Требуется решить уравнения 1)
.Требуется решить уравнения 1)  , 2)
, 2)  , 3)
, 3)  .
.
Решение.1)Вычислим определитель матрицы А:
 .
.
Так как  , то обратная матрица
, то обратная матрица  существует.
существует.
Умножим матричное уравнение на  слева и проведем преобразования с учетом свойств матричных операций:
слева и проведем преобразования с учетом свойств матричных операций:
 ,
,
 .
.
В результате получаем
 .
.
Находим обратную матрицу по формуле  , где
, где  – присоединенная матрица. Для этого вычисляем алгебраические дополнения элементов матрицы A:
– присоединенная матрица. Для этого вычисляем алгебраические дополнения элементов матрицы A:  ,
,  ,
,  ,
,  . Таким образом,
. Таким образом,  , т.е.
, т.е.
 .
.
Теперь вычисляем искомую матрицу  (решение рассматриваемого матричного уравнения):
(решение рассматриваемого матричного уравнения):

 .
.
Выполняем проверку:
 .
.
Проверка дала верное равенство, т.е. уравнение решено правильно.
2) Умножим матричное уравнение на  справа и проведем преобразования с учетом свойств матричных операций:
справа и проведем преобразования с учетом свойств матричных операций:
 ,
,
 .
.
В результате получаем формулу
 .
.
Так как  , то
, то

 .
.
Выполняем проверку:

 .
.
Вывод: уравнение решено верно.
3) Умножаем сначала матричное уравнение на  слева, а затем полученный результат – на
слева, а затем полученный результат – на  справа. В результате искомое решение уравнения выражается формулой
справа. В результате искомое решение уравнения выражается формулой
 .
.
Ищем  :
:
 ;
;  ;
; 
 .
.
Теперь имеем


 .
.
Остается осуществить проверку правильности полученного результата (сделайте это сами).
РЕШЕНИЕ ЗАДАЧ ТИПА 41–60
Задача1. Требуется, используя формулы Крамера, решить систему

Решение.Подсчитаем сначала главный определитель системы  , воспользовавшись его разложением по элементам первой строки:
, воспользовавшись его разложением по элементам первой строки:
 .
.
У нас

Так как  , делаем вывод о том, что система имеет единственное решение. Для его отыскания вычислим вспомогательные определители
, делаем вывод о том, что система имеет единственное решение. Для его отыскания вычислим вспомогательные определители 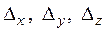 :
:

Далее, используя формулами Крамера, окончательно получаем:

Осуществим проверку правильности решения, подставив его в левую часть каждого уравнения заданной системы:

Все три равенства верные, поэтому делаем вывод о правильности полученного решения 
Задача 2.Решим систему уравнений из задачи 1 методом Гаусса последовательного исключения неизвестных.
1) Сначала умножим первое уравнение системы на  и результат сложим со вторым уравнением системы. Затем первое уравнение системы умножим на (–3) и результат сложим с третьим ее уравнением. В результате указанных тождественных преобразований система примет вид, в котором лишь первое уравнение будет содержать неизвестную величину x:
и результат сложим со вторым уравнением системы. Затем первое уравнение системы умножим на (–3) и результат сложим с третьим ее уравнением. В результате указанных тождественных преобразований система примет вид, в котором лишь первое уравнение будет содержать неизвестную величину x:

2) Займемся исключением неизвестной y из третьего уравнения последней системы. Для этого умножим второе ее уравнение на 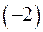 и сложим полученный результат с третьим уравнением. В результате получим новую систему, равносильную заданной:
и сложим полученный результат с третьим уравнением. В результате получим новую систему, равносильную заданной:

Теперь из третьего уравнения получаем  , затем из второго –
, затем из второго –  и наконец из первого –
и наконец из первого –  . Система решена.
. Система решена.
Задача 3. Cистему уравнений  записать в матричной форме и решить ее с помощью обратной матрицы.
записать в матричной форме и решить ее с помощью обратной матрицы.
Решение. Обозначим через  матрицу коэффициентов при неизвестных, через
матрицу коэффициентов при неизвестных, через  – матрицу-столбец неизвестных
– матрицу-столбец неизвестных  , а через
, а через  – матрицу-столбец свободных членов:
– матрицу-столбец свободных членов:
 ,
,  ,
,  .
.
С учетом этих обозначений данная система уравнений принимает следующую матричную форму:
 . (1)
. (1)
Если матрица  невырожденная, т.е. её определитель
невырожденная, т.е. её определитель  отличен от нуля, то она имеет обратную матрицу
отличен от нуля, то она имеет обратную матрицу  . Умножив обе части уравнения (1) слева на
. Умножив обе части уравнения (1) слева на  , получим
, получим
 ,
,
т.е.
 . (2)
. (2)
Равенство (2) называется матричной записью решения системы линейных уравнений. Для нахождения решения  системы уравнений (1) необходимо вычислить обратную матрицу
системы уравнений (1) необходимо вычислить обратную матрицу  .
.
Пусть имеем невырожденную матрицу
 .
.
Тогда обратная матрица определяется по формуле
 ,
,
где  (i=1, 2, 3; j=1, 2, 3) – алгебраическое дополнение элемента
(i=1, 2, 3; j=1, 2, 3) – алгебраическое дополнение элемента  в определителе матрицы
в определителе матрицы  , которое является произведением
, которое является произведением  на минор (определитель) второго порядка, полученный вычеркиванием i-й строки j-го столбца в определителе матрицы
на минор (определитель) второго порядка, полученный вычеркиванием i-й строки j-го столбца в определителе матрицы  .
.
Вычислим определитель  и алгебраические дополнения его элементов:
и алгебраические дополнения его элементов:
 , следовательно, матрица
, следовательно, матрица  имеет обратную матрицу
имеет обратную матрицу  ;
;
 ,
,  ,
,
 ,
,  ,
,
 ,
,  ,
,
 ,
,  ,
,
 .
.
Отсюда
 .
.
По формуле (2) находим решение данной системы уравнений в матричной форме:

Отсюда имеем  ,
,  ,
,  .
.
Остается сделать проверку, которую предлагаем сделать читателю самостоятельно.
|
из
5.00
|
Обсуждение в статье: РЕШЕНИЕ ЗАДАЧ ТИПА 41–60 |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

