 |
Главная |
Предел числовой последовательности
|
из
5.00
|
По аналогии с пределом функции в бесконечно удаленной точке вводится понятие предела последовательности.
Определение.
Число а называется пределом числовой последовательности  , если для любого
, если для любого 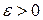 найдется такое натуральное число
найдется такое натуральное число  , что при всех
, что при всех  выполняется неравенство
выполняется неравенство
 .
.
Обозначают:
 или
или  при
при  .
.
Говорят также, что последовательность  сходится к а.
сходится к а.
Например, последовательность

с общим членом

имеет предел
 .
.
Бесконечно большие функции
Определение.
Функция  называется бесконечно большой при
называется бесконечно большой при 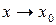
(или  ), если
), если
 или
или  при
при 
 .
.
Например, бесконечно большими функциями (б.б.ф.) являются:
 при
при  ;
;
 при
при  ;
;
 при
при  .
.
Различают частные случаи б.б.ф., когда, начиная с некоторого момента, б.б.ф. возрастая, принимает только положительные значения или, убывая, принимает только отрицательные значения.
Записывают это следующим образом:
 ,
,  .
.
Например,  ,
,  .
.
Бесконечно малые функции
Определение.
Функция  называется бесконечно малой при
называется бесконечно малой при 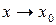
(или  ), если
), если
 .
.
Бесконечно малые функции (б.м.ф.) обозначают малыми греческими буквами α(х), β(х) и т.д.
Например,
 при
при  ;
;
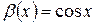 при
при  ;
;
 при
при  .
.
Между бесконечно большими и бесконечно малыми функциями существует простая связь, устанавливаемая следующей теоремой.
Теорема.
Если функция  есть бесконечно малая функция при
есть бесконечно малая функция при 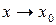 и в некоторой окрестности точки
и в некоторой окрестности точки 
 , то обратная величина
, то обратная величина  является бесконечно большой функцией при
является бесконечно большой функцией при 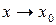 .
.
Справедлива и обратная теорема: величина, обратная всякой бесконечно большой, будет бесконечно малой.
Например,  при
при  есть б.м.ф., а
есть б.м.ф., а  при
при  − б.б.ф.
− б.б.ф.
Связь между функцией, ее пределом и бесконечно малой функцией
Сравнивая между собой определения предела функции в точке с определением бесконечно малой функции, можно заметить, что разность между функцией и ее пределом является величиной бесконечно малой.
Утверждение этого факта формулируют в двух теоремах − прямой и обратной.
Теорема (прямая).
Если функция  имеет предел, равный А, то ее можно представить как сумму числа А и бесконечно малой функции
имеет предел, равный А, то ее можно представить как сумму числа А и бесконечно малой функции  , т.е. если
, т.е. если 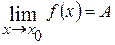 , то
, то
 .
.
 может принимать как положительные, так и отрицательные значения, т.е. функция
может принимать как положительные, так и отрицательные значения, т.е. функция  может быть как больше, так и меньше своего предела.
может быть как больше, так и меньше своего предела.
Теорема (обратная).
Если функцию  можно представить в виде суммы числа А и бесконечно малой функции
можно представить в виде суммы числа А и бесконечно малой функции  , то число А является пределом функции
, то число А является пределом функции  , т.е. если
, т.е. если  , то
, то
 .
.
Основные теоремы о пределах
Приведем без доказательства теоремы, которые облегчают нахождение пределов функций.
Пусть  и
и  − функции, для которых существуют пределы при
− функции, для которых существуют пределы при 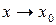 (или
(или  ), т.е.
), т.е.  и
и 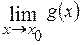 .
.
Теорема.
Если функция  постоянна, то ее предел равен ей самой:
постоянна, то ее предел равен ей самой:
 .
.
Теорема.
Предел суммы (разности) двух функций равен сумме (разности) их пределов:
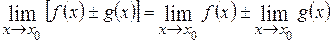 .
.
Следствие.
Функция может иметь только один предел при 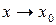 .
.
Теорема.
Предел произведения двух функций равен произведению их пределов:
 .
.
Следствие.
Постоянный множитель можно выносить за знак предела:
 .
.
Следствие.
Предел степени с натуральным показателем равен той же степени предела:
 .
.
Теорема.
Если предел функции  отличен от нуля, то предел обратной ей по величине функции
отличен от нуля, то предел обратной ей по величине функции  равен обратной величине предела данной функции:
равен обратной величине предела данной функции:
 .
.
Теорема.
Предел частного равен частному пределов, если предел знаменателя отличен от нуля:
 .
.
Теорема.
Если для функции  существует
существует  , то
, то
 .
.
|
из
5.00
|
Обсуждение в статье: Предел числовой последовательности |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

