 |
Главная |
Пример применения численного интегрирования
|
из
5.00
|
Вычислим, например, интеграл 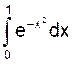 по формуле Симпсона с точностью до 0,001.
по формуле Симпсона с точностью до 0,001.
Чтобы выбрать необходимое для получения заданной точности число 2n, найдем f(4)(x). Последовательно дифференцируя функцию f(x)=  , получаем
, получаем
f(4)(x)=4  (4х4-12х2+3)
(4х4-12х2+3)
Так как на отрезке [0, 1]  £1, ½4х4-12х2+3½£5, то
£1, ½4х4-12х2+3½£5, то  . Следовательно, можно взять М=20. Используя формулу оценки погрешности, имеем 20/2880n4<1/1000(
. Следовательно, можно взять М=20. Используя формулу оценки погрешности, имеем 20/2880n4<1/1000(  ), откуда n4 >1000/144. Для того чтобы выполнялось это неравенство, достаточно взять n=2, т.е. 2n=4.
), откуда n4 >1000/144. Для того чтобы выполнялось это неравенство, достаточно взять n=2, т.е. 2n=4.
Разобьем теперь отрезок [0, 1] на четыре равные части точками х0=0, х1=1/4, х2=1/2, х3=3/4, х4=1 и вычислим приближенно значения функции f(x)=  в этих точках у0=1,0000, у1=0,9394, у2=0,7788, у3=0,5698, у4=0,3679. Применяя формулу Симпсона, получаем
в этих точках у0=1,0000, у1=0,9394, у2=0,7788, у3=0,5698, у4=0,3679. Применяя формулу Симпсона, получаем
 Таким образом,
Таким образом,  с точностью до 0,001. Итак, разбив отрезок [0, 1] всего на четыре равные части и заменив рассматриваемый интеграл суммой, стоящей в правой части формулы Симпсона, мы вычислили данный интеграл с необходимой точностью.
с точностью до 0,001. Итак, разбив отрезок [0, 1] всего на четыре равные части и заменив рассматриваемый интеграл суммой, стоящей в правой части формулы Симпсона, мы вычислили данный интеграл с необходимой точностью.
| Название метода | Формула | Порядок метода | Априорная погрешность вычислений | Апостериорная погрешность вычислений | |
| Левых прямоугольников (рис.1) | 
| 
| 

| 
| |
| Правых прямоугольников (рис.2) | 
| 
| 

| 
| |
| Средних прямоугольников | 
| 
| 

| 
| |
| Трапеций (рис.3) | 

| 
| 

| 
| |
| Симпсона (рис.4) | 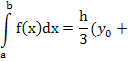

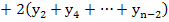

| 
| 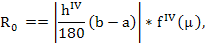

| 
|
Программная реализация в MatLab.
Вычисление определенного интеграла с помощью встроенной функции.
>> syms x
>> I = double(int((x^2-6.5)/(x^3+sin(7.8*x)),3.6,5.4))
>>
I =
0.26649340577279
Программный блок, реализующий приближенное вычисление определенного интеграла.
function res = f(x);
res = (x^2+1.8)/(x^3+7.9);
end
----------------------
function res = Integral(str, a , b, n);
%str - methods name, a,b - distance, n - number of points
h = (b-a)/n;
Sum = 0;
switch (str)
case 'Simpson'
q1=0; q2=0;
for i = 1:n-1
if (mod(i,2)==1)
q1 = q1+f(a + i*h);
else q2 = q2+f(a + i*h);
end;
end;
Sum =(h/3)*( f(a) + 4*q1 + 2*q2 + f(b));
case 'Trapezium'
for i = 1:n-1
Sum = Sum + f(a + i*h);
end;
Sum = (h/2)*( f(a) + 2*Sum + f(b));
case 'LeftRectangles'
for i=1:n-1
Sum = Sum + h*f(a + i*h);
end;
Sum = h*f(a) + Sum;
case 'RightRectangles'
for i=1:n-1
Sum = Sum + h*f(a + i*h);
end;
Sum = h*f(b) + Sum;
case 'MediumRectangles'
for i=1:n
Sum = Sum + h*f(((a + (i-1)*h)+(a + i*h))/2);
end;
otherwise
error('This is impossible value')
end
res = Sum;
return
Программный блок вычисления апостериорных погрешностей вычислений.
function res = Priori_Error(str,a,b,n);
switch (str)
case 'Simpson'
R = abs(Integral(str,a,b,n)-Integral(str,a,b,0.5*n))/15;
case 'Trapezium'
R = abs(Integral(str,a,b,n)-Integral(str,a,b,0.5*n))/3;
case 'LeftRectangles'
R = abs(Integral(str,a,b,n)-Integral(str,a,b,0.5*n));
case 'RightRectangles'
R = abs(Integral(str,a,b,n)-Integral(str,a,b,0.5*n));
case 'MediumRectangles'
R = abs(Integral(str,a,b,n)-Integral(str,a,b,0.5*n))/3;
otherwise
error('This is impossible value')
end;
res = R;
return
Результаты вычислений
>> format long
>> IS = Integral('Simpson',3.6,5.4,12)
IS =
0.26649801994399
>> IT = Integral('Trapezium',3.6,5.4,12)
IT =
0.26635817701576
>> ILR = Integral('LeftRectangles',3.6,5.4,12)
ILR =
0.26584089261870
>> IRR = Integral('RightRectangles',3.6,5.4,12)
IRR =
0.26687546141281
>> IMR = Integral('MediumRectangles',3.6,5.4,12)
IMR =
0.26656137337914
>> Priori_ErrorIS = Priori_Error('Simpson',3.6,5.4,12)
Priori_ErrorIS =
1.040388407134533e-005
>> Priori_ErrorIT = Priori_Error('Trapezium',3.6,5.4,12)
Priori_ErrorIT =
1.398429282359707e-004
>> Priori_ErrorILR = Priori_Error('LeftRectangles',3.6,5.4,12)
Priori_ErrorILR =
9.368131817630854e-004
>> Priori_ErrorIRR = Priori_Error('RightRectangles',3.6,5.4,12)
Priori_ErrorIRR =
9.775561234709462e-005
>> Priori_ErrorIMR = Priori_Error('MediumRectangles',3.6,5.4,12)
Priori_ErrorIMR =
7.211080710719149e-005
| Приближенное вычисление определенных интегралов" |

|
| Исходные данные: |
| ; |

|
| Промежуток интегрирования [a,b] : |

|

|
| 1. Табулирование функции на заданном промежутке [a,b]. |

|

|

|

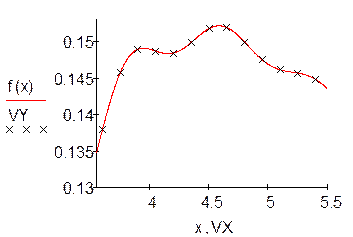
|
| 2. Вычисление определенного интеграла с помощью стандартной функции. |

|
| 3. Программный блок, реализующий вычисление приближенного значения определенного интеграла. 1. Формула Симпсона. 2. Формула трапеций. 3. Формула средних прямоугольников. 4. Формула правых прямоугольников. 5. Формула левых прямоугольников. |
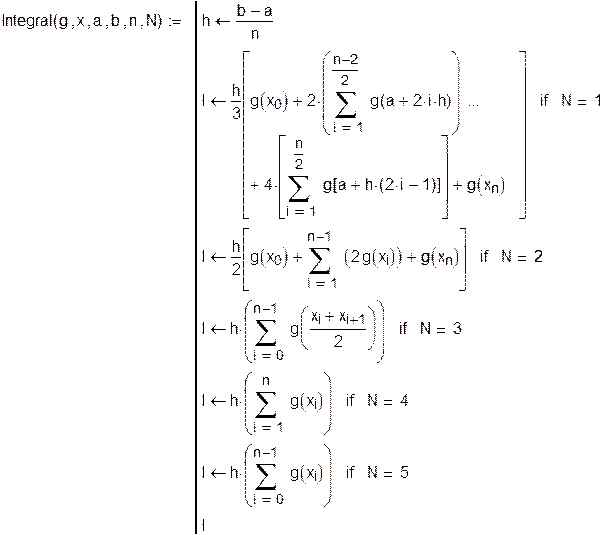
|
| Результаты вычислений для шага h и 2h |
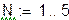
|

|

|
4. Вычисление апостериорной погрешности приближенного вычисления определенного интеграла по формулам 1-5.
Программный блок 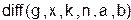 , где
-g(u) - исходная функция;
-x - вектор узловых точек;
- , где
-g(u) - исходная функция;
-x - вектор узловых точек;
- 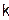 - порядок метода;
вычисляет значения - порядок метода;
вычисляет значения 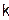 -ой производной функции g(u) в
узловых точках. -ой производной функции g(u) в
узловых точках.
|

|
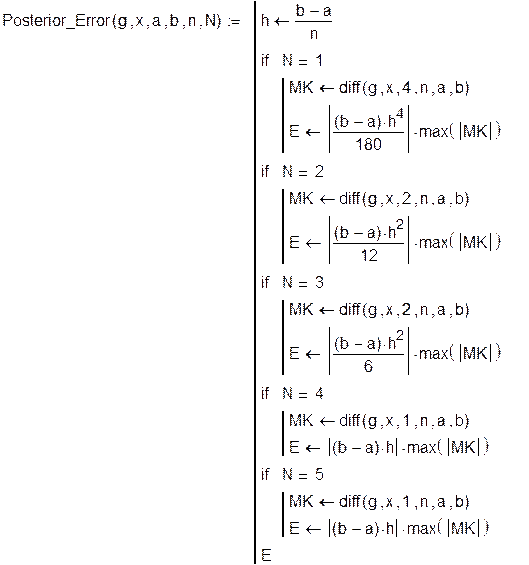
|
| 5. Априорные погрешности приближенного вычисления определенного интеграла по формулам 1-5. - g(x) - подынтегральная функция; - x - узловые точки; - k - порядок метода N; |

|

|

|
Варианты заданий
| Номер варианта | Интеграл | Номер варианта | Интеграл |
|
из
5.00
|
Обсуждение в статье: Пример применения численного интегрирования |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

