 |
Главная |
Теория нелинейных систем автоматического управления_каз
|
из
5.00
|
Выходная величина системы второго порядка изменяется следующим образом 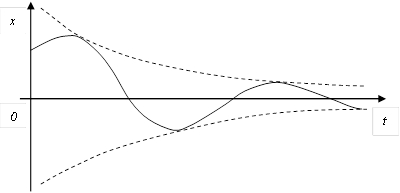 о системе можно сказать следующее:B) Характеристическое уравнение имеет комплексно – сопряженные корни с отрицательной вещественной частью D) Фазовый портрет системы
о системе можно сказать следующее:B) Характеристическое уравнение имеет комплексно – сопряженные корни с отрицательной вещественной частью D) Фазовый портрет системы  G) Особая точка устойчивый фокус
G) Особая точка устойчивый фокус
Выходная величина системы второго порядка изменяется следующим образом 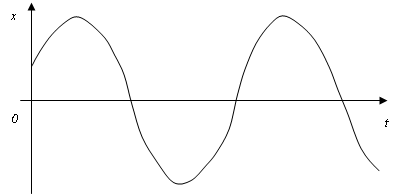 о системе можно сказать следующее: A) Характеристическое уравнение имеет два чисто мнимых комплексно – сопряженных корня F) Фазовый портрет системы
о системе можно сказать следующее: A) Характеристическое уравнение имеет два чисто мнимых комплексно – сопряженных корня F) Фазовый портрет системы 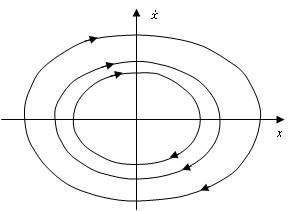 G) Особая точка центр
G) Особая точка центр
Выходная величина системы второго порядка изменяется следующим образом  о системе можно сказать следующее: C) Характеристическое уравнение имеет комплексно – сопряженные корни с положительной вещественной частьюE) Фазовый портрет системы
о системе можно сказать следующее: C) Характеристическое уравнение имеет комплексно – сопряженные корни с положительной вещественной частьюE) Фазовый портрет системы  H) Особая точка неустойчивый фокус
H) Особая точка неустойчивый фокус
Выходная величина системы второго порядка изменяется следующим образом 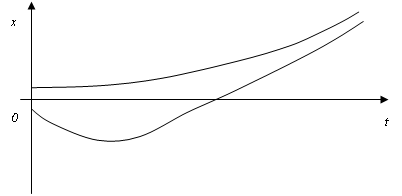 о системе можно сказать следующее: B) Характеристическое уравнение имеет два положительных корняE) Фазовый портрет системы
о системе можно сказать следующее: B) Характеристическое уравнение имеет два положительных корняE) Фазовый портрет системы  H) Особая точка неустойчивый узел
H) Особая точка неустойчивый узел
Выходная величина системы второго порядка изменяется следующим образом 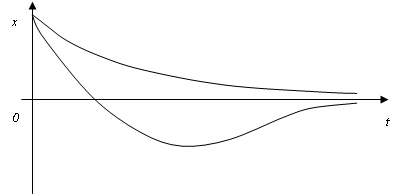 о системе можно сказать следующее: A) Характеристическое уравнение имеет два отрицательных корня D) Фазовый портрет системы
о системе можно сказать следующее: A) Характеристическое уравнение имеет два отрицательных корня D) Фазовый портрет системы 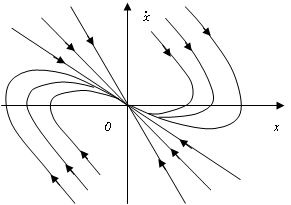 G) Особая точка устойчивый узел
G) Особая точка устойчивый узел
Выходная величина системы второго порядка изменяется следующим образом  о системе можно сказать следующее: G) Особая точка центр
о системе можно сказать следующее: G) Особая точка центр
Дан график решетчатой функции  A) первая прямая разность равна
A) первая прямая разность равна  D) первая прямая разность равна
D) первая прямая разность равна 
Дан график решетчатой функции 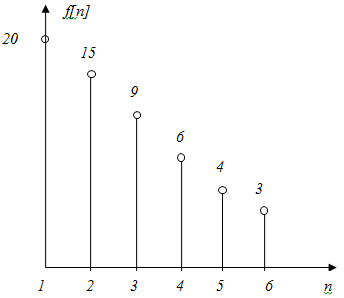 B) первая прямая разность равна
B) первая прямая разность равна 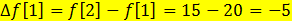
Дан график решетчатой функции  B) первая прямая разность равна
B) первая прямая разность равна 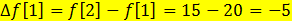 D) прямая разность второго порядка равна
D) прямая разность второго порядка равна 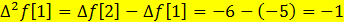
Дан график решетчатой функции  A)
A)  D) t wx:val="Cambria Math"/><w:i/><w:highlight w:val="yellow"/><w:lang w:val="KZ"/></w:rPr><m:t>1</m:t></m:r></m:e></m:d><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:highlight w:val="yellow"/><w:lang w:val="KZ"/></w:rPr><m:t>=4</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
D) t wx:val="Cambria Math"/><w:i/><w:highlight w:val="yellow"/><w:lang w:val="KZ"/></w:rPr><m:t>1</m:t></m:r></m:e></m:d><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:highlight w:val="yellow"/><w:lang w:val="KZ"/></w:rPr><m:t>=4</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 
Дан график решетчатой функции  A)
A) 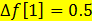 G) t wx:val="Cambria Math"/><w:i/><w:highlight w:val="yellow"/><w:lang w:val="KZ"/></w:rPr><m:t>1</m:t></m:r></m:e></m:d><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:highlight w:val="yellow"/><w:lang w:val="KZ"/></w:rPr><m:t>=</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
G) t wx:val="Cambria Math"/><w:i/><w:highlight w:val="yellow"/><w:lang w:val="KZ"/></w:rPr><m:t>1</m:t></m:r></m:e></m:d><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:highlight w:val="yellow"/><w:lang w:val="KZ"/></w:rPr><m:t>=</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 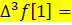 0.5
0.5
Дан график решетчатой функции  A) прямая разность второго порядка равна
A) прямая разность второго порядка равна 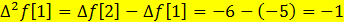 D) прямая разность третьего порядка равна
D) прямая разность третьего порядка равна 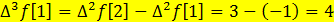
Дан график решетчатой функции  B) первая прямая разность равна
B) первая прямая разность равна  G) прямая разность третьего порядка равна
G) прямая разность третьего порядка равна 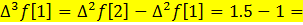 0.5
0.5
Дан график решетчатой функции  C)
C)  D)
D) 
Дан график решетчатой функции  D) прямая разность третьего порядка равна
D) прямая разность третьего порядка равна 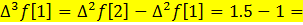 0.5 G) прямая разность четвертого порядка равна
0.5 G) прямая разность четвертого порядка равна 
Дан график решетчатой функции 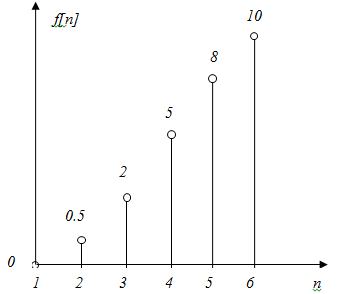 F)
F) 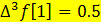 G)
G) 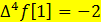
Дана любая решетчатая функция  A) первая прямая разность равна
A) первая прямая разность равна  D) прямая разность второго порядка равна
D) прямая разность второго порядка равна  G) прямая разность третьего порядка равна
G) прямая разность третьего порядка равна 
Даны значения решетчатой функции  ,
,  ,
,  ,
,  . B) первая прямая разность равна
. B) первая прямая разность равна 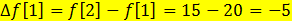
Даны значения решетчатой функции  ,
,  ,
,  ,
,  ,
, 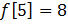 A)
A) 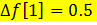 G) t wx:val="Cambria Math"/><w:i/><w:highlight w:val="yellow"/><w:lang w:val="KZ"/></w:rPr><m:t>1</m:t></m:r></m:e></m:d><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:highlight w:val="yellow"/><w:lang w:val="KZ"/></w:rPr><m:t>=</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
G) t wx:val="Cambria Math"/><w:i/><w:highlight w:val="yellow"/><w:lang w:val="KZ"/></w:rPr><m:t>1</m:t></m:r></m:e></m:d><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:highlight w:val="yellow"/><w:lang w:val="KZ"/></w:rPr><m:t>=</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 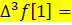 0.5
0.5
Даны значения решетчатой функции  ,
,  ,
,  ,
,  ,
, 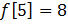 B) первая прямая разность равна
B) первая прямая разность равна  G) ) прямая разность третьего порядка равна
G) ) прямая разность третьего порядка равна 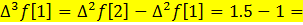 0.5
0.5
Даны значения решетчатой функции  ,
,  ,
,  ,
,  ,
, 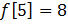 ,
, 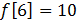 D ) прямая разность третьего порядка равна
D ) прямая разность третьего порядка равна 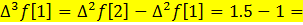 0.5G) прямая разность четвертого порядка равна
0.5G) прямая разность четвертого порядка равна 
Даны значения решетчатой функции  ,
,  ,
,  ,
,  ,
, 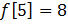 ,
, 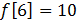 F)
F) 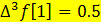 G)
G) 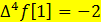
Даны значения решетчатой функции  ,
,  ,
,  ,
,  ,
, 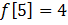 . A)
. A)  D) t wx:val="Cambria Math"/><w:i/><w:highlight w:val="yellow"/><w:lang w:val="KZ"/></w:rPr><m:t>1</m:t></m:r></m:e></m:d><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:highlight w:val="yellow"/><w:lang w:val="KZ"/></w:rPr><m:t>=4</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
D) t wx:val="Cambria Math"/><w:i/><w:highlight w:val="yellow"/><w:lang w:val="KZ"/></w:rPr><m:t>1</m:t></m:r></m:e></m:d><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:highlight w:val="yellow"/><w:lang w:val="KZ"/></w:rPr><m:t>=4</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 
Даны значения решетчатой функции  ,
,  ,
,  ,
,  ,
, 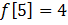 . A) прямая разность второго порядка равна
. A) прямая разность второго порядка равна 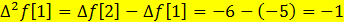 D) ) прямая разность третьего порядка равна
D) ) прямая разность третьего порядка равна 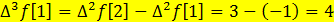
Даны значения решетчатой функции  ,
,  ,
,  ,
,  ,
, 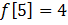 . B) первая прямая разность равна
. B) первая прямая разность равна 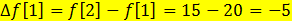 D) прямая разность второго порядка равна
D) прямая разность второго порядка равна 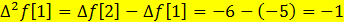
Даны значения решетчатой функции  ,
,  ,
,  ,
,  ,
, 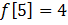 . C)
. C)  D)
D) 
Даны значения решетчатой функции  ,
,  ,
,  ,
,  . A) первая прямая разность равна
. A) первая прямая разность равна  D) первая прямая разность равна
D) первая прямая разность равна 
Динамика системы описывается следующей системой дифференциальных уравнений  тогдаХарактеристическое уравнение
тогдаХарактеристическое уравнение  D) Корни характеристического уравнения равны
D) Корни характеристического уравнения равны 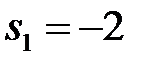 ,
, 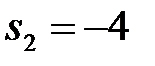 .G) Особая точка устойчивый узел
.G) Особая точка устойчивый узел
Динамика системы описывается следующей системой дифференциальных уравнений 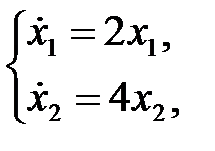 тогдаC) Характеристическое уравнение
тогдаC) Характеристическое уравнение  F) Корни характеристического уравнения равны
F) Корни характеристического уравнения равны 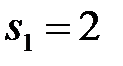 ,
,  .H) Особая точка неустойчивый узел
.H) Особая точка неустойчивый узел
Динамика системы описывается следующей системой дифференциальных уравнений 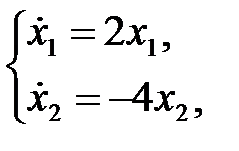 тогдаB) Характеристическое уравнение
тогдаB) Характеристическое уравнение  E) Корни характеристического уравнения равны
E) Корни характеристического уравнения равны 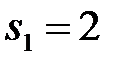 ,
,  .G) Особая точка седло
.G) Особая точка седло
Динамика системы описывается следующей системой дифференциальных уравнений  тогда B) Характеристическое уравнение
тогда B) Характеристическое уравнение  E) Корни характеристического уравнения равны
E) Корни характеристического уравнения равны  ,
, 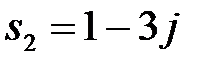 . H) Особая точка неустойчивый фокус
. H) Особая точка неустойчивый фокус
Динамика системы описывается следующей системой дифференциальных уравнений  тогдаC) Характеристическое уравнение
тогдаC) Характеристическое уравнение  F) Корни характеризующего уравнения равно
F) Корни характеризующего уравнения равно  ,
,  .G) Особая точка центр
.G) Особая точка центр
Если процессы, происходящие в нелинейной системе выглядят  то B) Неустойчивые автоколебания системы с амплитудой а, F) Если начальные условия будут в промежутке а, то при уменьшении амплитуды колебаний система будет «устойчива в малом» , H) Если начальные условия будут вне промежутка а, то система будет «неустойчива в большом»
то B) Неустойчивые автоколебания системы с амплитудой а, F) Если начальные условия будут в промежутке а, то при уменьшении амплитуды колебаний система будет «устойчива в малом» , H) Если начальные условия будут вне промежутка а, то система будет «неустойчива в большом»
Если процессы, происходящие в нелинейной системе выглядят 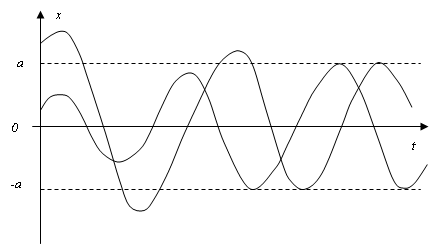 то D) В равновесном состоянии колебательно неустойчива,E) Если начальные условия будут в промежутке а, то при увеличении амплитуды колебаний в системе имеют место устойчивые автоколебания с амплитудой а, G) Если начальные условия будут вне промежутка а, то при уменьшении амплитуды автоколебаний в системе имеют место устойчивые автоколебания с амплитудой а
то D) В равновесном состоянии колебательно неустойчива,E) Если начальные условия будут в промежутке а, то при увеличении амплитуды колебаний в системе имеют место устойчивые автоколебания с амплитудой а, G) Если начальные условия будут вне промежутка а, то при уменьшении амплитуды автоколебаний в системе имеют место устойчивые автоколебания с амплитудой а
Исследуя устойчивость нелинейной системы по теореме В.М.Попова на абсолютную устойчивость, по известной передаточной функции  линейной части надо выполнить следующееA) Действительную часть видоизмененной частотной характеристики находим следующим образом
линейной части надо выполнить следующееA) Действительную часть видоизмененной частотной характеристики находим следующим образом  F) Действительную часть видоизмененной частотной характеристики находим следующим образом
F) Действительную часть видоизмененной частотной характеристики находим следующим образом 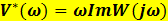 G) Условие абсолютной устойчивости системы :
G) Условие абсолютной устойчивости системы : 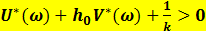
Корни характеристического уравнения системы второго порядка на комплексной плоскости расположены следующим образом 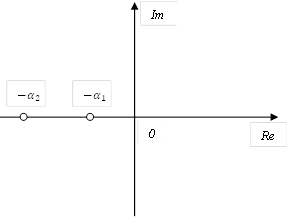 A) Уравнение выходной величины
A) Уравнение выходной величины  E) Выходная величина изменяется следующим образом
E) Выходная величина изменяется следующим образом 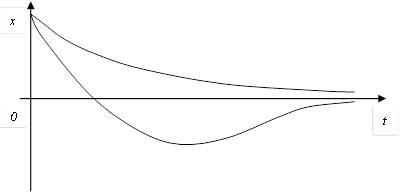 G) Особая точка устойчивый узел
G) Особая точка устойчивый узел
Корни характеристического уравнения системы второго порядка на комплексной плоскости расположены следующим образом 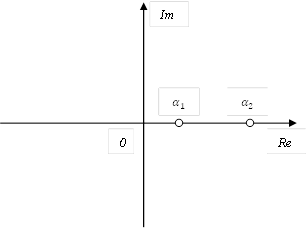 A) Уравнение выходной величины
A) Уравнение выходной величины  F) ) Выходная величина изменяется следующим образом
F) ) Выходная величина изменяется следующим образом 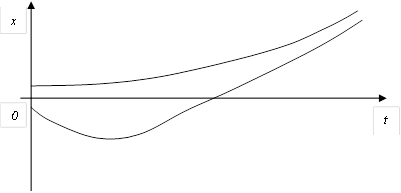 H) Особая точка неустойчивый узел
H) Особая точка неустойчивый узел
Корни характеристического уравнения системы второго порядка на комплексной плоскости расположены следующим образом  B) Уравнение выходной величины
B) Уравнение выходной величины  D) Выходная величина изменяется следующим образом
D) Выходная величина изменяется следующим образом 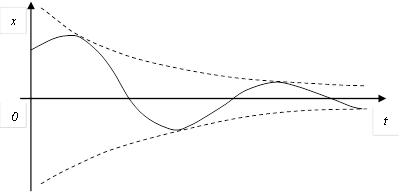 G) ) Особая точка устойчивый фокус
G) ) Особая точка устойчивый фокус
Корни характеристического уравнения системы второго порядка на комплексной плоскости расположены следующим образом  C) Уравнение выходной величины
C) Уравнение выходной величины 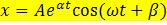 F) Выходная величина изменяется следующим образом
F) Выходная величина изменяется следующим образом  H) Особая точка неустойчивый фокус
H) Особая точка неустойчивый фокус
Корни характеристического уравнения системы второго порядка на комплексной плоскости расположены следующим образом  C) Уравнение выходной величины
C) Уравнение выходной величины  D) Выходная величина изменяется следующим образом
D) Выходная величина изменяется следующим образом 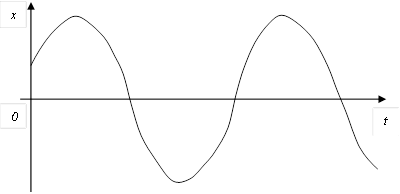 G) Особая точка центр
G) Особая точка центр
Корни характеристического уравнения системы второго порядка на комплексной плоскости расположены следующим образом  B) Уравнение выходной величины
B) Уравнение выходной величины  E) Выходная величина изменяется следующим образом
E) Выходная величина изменяется следующим образом  G) Особая точка седло
G) Особая точка седло
Корни характеристического уравнения системы второго порядка на комплексной плоскости расположены следующим образом 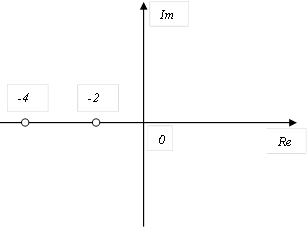 A) Уравнение выходной величины
A) Уравнение выходной величины  E) Выходная величина изменяется следующим образом
E) Выходная величина изменяется следующим образом  G) Особая точка устойчивый узел
G) Особая точка устойчивый узел
Корни характеристического уравнения системы второго порядка на комплексной плоскости расположены следующим образом 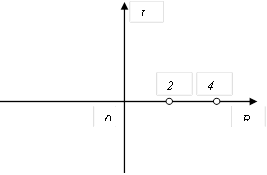 A) Уравнение выходной величины
A) Уравнение выходной величины  F) Выходная величина изменяется следующим образом
F) Выходная величина изменяется следующим образом  H) Особая точка неустойчивый узел
H) Особая точка неустойчивый узел
Корни характеристического уравнения системы второго порядка на комплексной плоскости расположены следующим образом  B) Уравнение выходной величины
B) Уравнение выходной величины  D) Выходная величина изменяется следующим образом
D) Выходная величина изменяется следующим образом  G) Особая точка устойчивый фокус
G) Особая точка устойчивый фокус
Корни характеристического уравнения системы второго порядка на комплексной плоскости расположены следующим образом 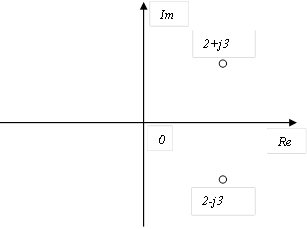 C) Уравнение выходной величины
C) Уравнение выходной величины  F) Выходная величина изменяется следующим образом
F) Выходная величина изменяется следующим образом  H) Особая точка неустойчивый фокус
H) Особая точка неустойчивый фокус
Корни характеристического уравнения системы второго порядка на комплексной плоскости расположены следующим образом 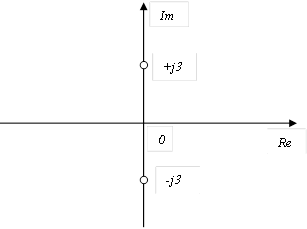 C) Уравнение выходной величины
C) Уравнение выходной величины 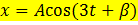 D) Выходная величина изменяется следующим образом
D) Выходная величина изменяется следующим образом  G) Особая точка центр
G) Особая точка центр
Корни характеристического уравнения системы второго порядка на комплексной плоскости расположены следующим образом  B) Уравнение выходной величины
B) Уравнение выходной величины 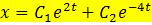 E) Выходная величина изменяется следующим образом
E) Выходная величина изменяется следующим образом  G) Особая точка седло
G) Особая точка седло
Корни характеристического уравнения системы второго порядка равны  ,
, 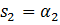 , тогда А) Уравнение выходной величины
, тогда А) Уравнение выходной величины  F) Выходная величина изменяется следующим образом
F) Выходная величина изменяется следующим образом 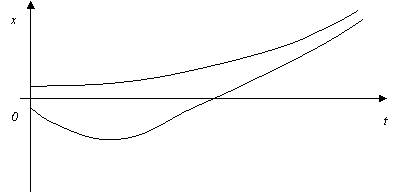 H) Особая точка неустойчивый узел
H) Особая точка неустойчивый узел
Корни характеристического уравнения системы второго порядка равны  ,
,  , тогда B)Уравнение выходной величины
, тогда B)Уравнение выходной величины  E)Выходная величина изменяется следующим образом
E)Выходная величина изменяется следующим образом 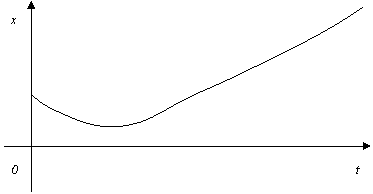 G) Особая точка седло
G) Особая точка седло
Корни характеристического уравнения системы второго порядка равны 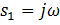 ,
,  , тогда C)Уравнение выходной величины
, тогда C)Уравнение выходной величины  D)Выходная величина изменяется следующим образом
D)Выходная величина изменяется следующим образом 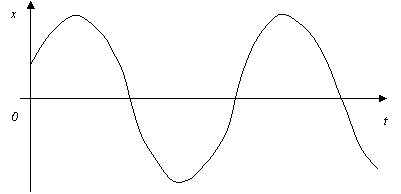 G)Особая точка центр
G)Особая точка центр
Корни характеристического уравнения системы второго порядка равны 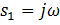 ,
,  , тогдаC) Уравнение выходной величины
, тогдаC) Уравнение выходной величины  D) Выходная величина изменяется следующим образом
D) Выходная величина изменяется следующим образом  G) Особая точка центр
G) Особая точка центр
Корни характеристического уравнения системы второго порядка равны  ,
, 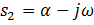 , тогдаC) Уравнение выходной величины
, тогдаC) Уравнение выходной величины 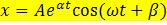 F) Выходная величина изменяется следующим образом
F) Выходная величина изменяется следующим образом  H) Особая точка неустойчивый фокус
H) Особая точка неустойчивый фокус
Корни характеристического уравнения системы второго порядка равны  ,
, 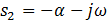 , тогда B) Уравнение выходной величины
, тогда B) Уравнение выходной величины  D) Выходная величина изменяется следующим образом
D) Выходная величина изменяется следующим образом  G) Особая точка устойчивый фокус
G) Особая точка устойчивый фокус
Корни характеристического уравнения системы второго порядка равны 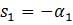 ,
,  , тогда A) Уравнение выходной величины
, тогда A) Уравнение выходной величины  E) Выходная величина изменяется следующим образом
E) Выходная величина изменяется следующим образом 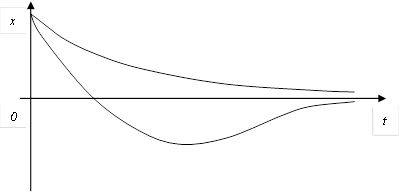 G) Особая точка устойчивый узел
G) Особая точка устойчивый узел
Корни характеристического уравнения системы второго порядка равны  ,
, 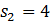 , тогда A) Уравнение выходной величины
, тогда A) Уравнение выходной величины  F) Выходная величина изменяется следующим образом
F) Выходная величина изменяется следующим образом 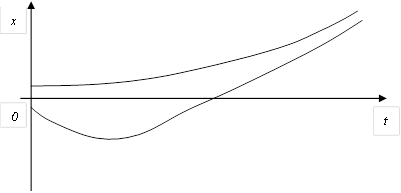 H) Особая точка неустойчивый узел
H) Особая точка неустойчивый узел
Корни характеристического уравнения системы второго порядка равны  ,
,  , тогда B) Уравнение выходной величины
, тогда B) Уравнение выходной величины 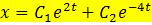 E) Выходная величина изменяется следующим образом
E) Выходная величина изменяется следующим образом  G) Особая точка седло
G) Особая точка седло
Корни характеристического уравнения системы второго порядка равны 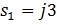 ,
, 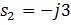 , тогдаC) Уравнение выходной величины
, тогдаC) Уравнение выходной величины 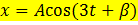 D) Выходная величина изменяется следующим образом
D) Выходная величина изменяется следующим образом  G) Особая точка центр
G) Особая точка центр
Корни характеристического уравнения системы второго порядка равны  ,
,  , онда C) Уравнение выходной величины
, онда C) Уравнение выходной величины  F) Выходная величина изменяется следующим образом
F) Выходная величина изменяется следующим образом 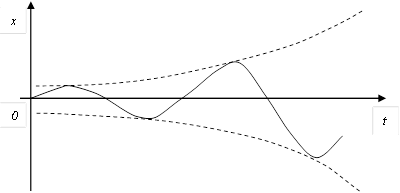 H) Особая точка неустойчивый фокус
H) Особая точка неустойчивый фокус
Корни характеристического уравнения системы второго порядка равны 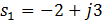 ,
,  , тогдаB) Уравнение выходной величины
, тогдаB) Уравнение выходной величины  D) Выходная величина изменяется следующим образом
D) Выходная величина изменяется следующим образом  G) Особая точка устойчивый фокус
G) Особая точка устойчивый фокус
Корни характеристического уравнения системы второго порядка равны 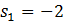 ,
,  , тогда A) Уравнение выходной величины
, тогда A) Уравнение выходной величины  E) Выходная величина изменяется следующим образом
E) Выходная величина изменяется следующим образом  G) Особая точка устойчивый узел
G) Особая точка устойчивый узел
Нелинейная система описывается системой дифференциальных уравнений  Функцию Ляпунова выбираем такой
Функцию Ляпунова выбираем такой 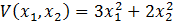 , Устойчивость системы исследуется следующим образом A) Производная функции Ляпунова вычисляется следующим образом
, Устойчивость системы исследуется следующим образом A) Производная функции Ляпунова вычисляется следующим образом  E) Производная функции Ляпунова равна
E) Производная функции Ляпунова равна 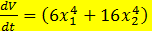 H) Функция Ляпунова положительная знакоопределенная, а ее производная положительная знакоопределенная функция, поэтому система неустойчива
H) Функция Ляпунова положительная знакоопределенная, а ее производная положительная знакоопределенная функция, поэтому система неустойчива
Нелинейная система описывается системой дифференциальных уравнений 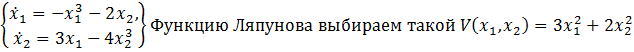 , Устойчивость системы исследуется следующим образом A) Производная функции Ляпунова вычисляется следующим образом
, Устойчивость системы исследуется следующим образом A) Производная функции Ляпунова вычисляется следующим образом  D) Производная функции Ляпунова равна
D) Производная функции Ляпунова равна  G) Функция Ляпунова положительная знакоопределенная, а ее производная отрицательная знакоопределенная функция, поэтому система асимптотически устойчива
G) Функция Ляпунова положительная знакоопределенная, а ее производная отрицательная знакоопределенная функция, поэтому система асимптотически устойчива
Нелинейная система описывается системой дифференциальных уравнений 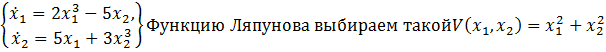 ,Устойчивость системы исследуется следующим образом A) Производная функции Ляпунова вычисляется следующим образом
,Устойчивость системы исследуется следующим образом A) Производная функции Ляпунова вычисляется следующим образом  E) Производная функции Ляпунова равна
E) Производная функции Ляпунова равна  H) Функция Ляпунова положительная знакоопределенная, а ее производная положительная знакоопределенная функция, поэтому система неустойчива
H) Функция Ляпунова положительная знакоопределенная, а ее производная положительная знакоопределенная функция, поэтому система неустойчива
Нелинейная система описывается системой дифференциальных уравнений  Функцию Ляпунова выбираем такой >
Функцию Ляпунова выбираем такой > 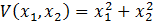 , Устойчивость системы исследуется следующим образом A) Производная функции Ляпунова вычисляется следующим образом
, Устойчивость системы исследуется следующим образом A) Производная функции Ляпунова вычисляется следующим образом  D) Производная функции Ляпунова равна
D) Производная функции Ляпунова равна  G) Функция Ляпунова положительная знакоопределенная, а ее производная отрицательная знакоопределенная функция, поэтому система асимптотически устойчива
G) Функция Ляпунова положительная знакоопределенная, а ее производная отрицательная знакоопределенная функция, поэтому система асимптотически устойчива
Нелинейная система описывается системой дифференциальных уравнений 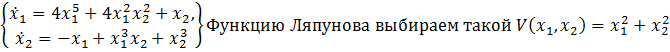 , Устойчивость системы исследуется следующим образом A) Производная функции Ляпунова вычисляется следующим образомr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
, Устойчивость системы исследуется следующим образом A) Производная функции Ляпунова вычисляется следующим образомr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 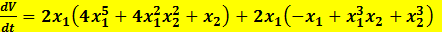 E) Производная функции Ляпунова равна
E) Производная функции Ляпунова равна  H) Функция Ляпунова положительная знакоопределенная, а ее производная положительная знакопостоянная функция, поэтому система неустойчива
H) Функция Ляпунова положительная знакоопределенная, а ее производная положительная знакопостоянная функция, поэтому система неустойчива
Нелинейная система описывается системой дифференциальных уравнений 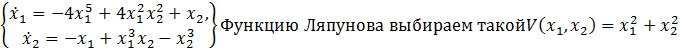 , Устойчивость системы исследуется следующим образомA)Производная функции Ляпунова вычисляется следующим образом
, Устойчивость системы исследуется следующим образомA)Производная функции Ляпунова вычисляется следующим образом  D) Производная функции Ляпунова равна
D) Производная функции Ляпунова равна  G) Функция Ляпунова положительная знакоопределенная, а ее производная отрицательная знакопостоянная функция, поэтому система устойчива
G) Функция Ляпунова положительная знакоопределенная, а ее производная отрицательная знакопостоянная функция, поэтому система устойчива
Нелинейная система описывается системой дифференциальных уравнений  ,Устойчивость системы исследуется следующим образом B) Производная функции Ляпунова вычисляется следующим образом
,Устойчивость системы исследуется следующим образом B) Производная функции Ляпунова вычисляется следующим образом  E) Производная функции Ляпунова равна
E) Производная функции Ляпунова равна 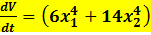 H) Функция Ляпунова положительная знакоопределенная, а ее производная положительная знакоопределенная функция, поэтому система неустойчива
H) Функция Ляпунова положительная знакоопределенная, а ее производная положительная знакоопределенная функция, поэтому система неустойчива
Нелинейная система описывается системой дифференциальных уравнений  , Устойчивость системы исследуется следующим образом A) Производная функции Ляпунова вычисляется следующим образом
, Устойчивость системы исследуется следующим образом A) Производная функции Ляпунова вычисляется следующим образом  D) Производная функции Ляпунова равна
D) Производная функции Ляпунова равна 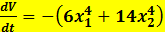 G) Функция Ляпунова положительная знакоопределенная, а ее производная отрицательная знакоопределенная функция, поэтому система асимптотически устойчива
G) Функция Ляпунова положительная знакоопределенная, а ее производная отрицательная знакоопределенная функция, поэтому система асимптотически устойчива
Об импульсной системе можно сказать следующее B) в структуре имеется импульсное звено C) импульсное звено преобразует непрерывный сигнал в дискретный сигнал E) описываются обыкновенными дифференциальными уравнениями
При исследовании устойчивости нелинейной системы по теореме В.М.Попова на абсолютную устойчивость передаточная функция линейной части  , тогда о системе можно сказать следующееA) Действительная часть видоизмененной частотной характеристики равна
, тогда о системе можно сказать следующееA) Действительная часть видоизмененной частотной характеристики равна 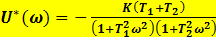 D) Мнимая часть видоизмененной частотной характеристики равна
D) Мнимая часть видоизмененной частотной характеристики равна  G) Условие абсолютной устойчивости системы :
G) Условие абсолютной устойчивости системы : 
При исследовании устойчивости нелинейной системы по теореме В.М.Попова на абсолютную устойчивость передаточная функция линейной части  , тогда о системе можно сказать следующееA) Действительная часть видоизмененной частотной характеристики равна
, тогда о системе можно сказать следующееA) Действительная часть видоизмененной частотной характеристики равна  D) Мнимая часть видоизмененной частотной характеристики равна
D) Мнимая часть видоизмененной частотной характеристики равна 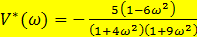 G) Условие абсолютной устойчивости системы :
G) Условие абсолютной устойчивости системы : 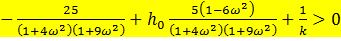
При исследовании устойчивости нелинейной системы функция Ляпунова  Тогда можно сказать следующее: A) Функция Ляпунова положительная знакоопределенная функция D) Производная функции Ляпунова положительная знакоопределенная функция H) Функция Ляпунова положительная знакоопределенная, а ее производная положительная знакоопределенная функция, поэтому система неустойчива
Тогда можно сказать следующее: A) Функция Ляпунова положительная знакоопределенная функция D) Производная функции Ляпунова положительная знакоопределенная функция H) Функция Ляпунова положительная знакоопределенная, а ее производная положительная знакоопределенная функция, поэтому система неустойчива
При исследовании устойчивости нелинейной системы функция Ляпунова 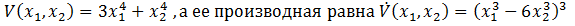 . Тогда можно сказать следующее:A) Функция Ляпунова положительная знакоопределенная функция F) Производная функции Ляпунова знакопеременная функция H) Функция Ляпунова положительная знакоопределенная, а ее производная знакопеременная функция, поэтому мы не можем определить система устойчива или неустойчива
. Тогда можно сказать следующее:A) Функция Ляпунова положительная знакоопределенная функция F) Производная функции Ляпунова знакопеременная функция H) Функция Ляпунова положительная знакоопределенная, а ее производная знакопеременная функция, поэтому мы не можем определить система устойчива или неустойчива
При исследовании устойчивости нелинейной системы функция Ляпунова  Тогда можно сказать следующее: A) Функция Ляпунова положительная знакоопределенная функцияD) Производная функции Ляпунова положительная знакоопределенная функция H) Функция Ляпунова положительная знакоопределенная, а ее производная положительная знакопостоянная функция, поэтому система неустойчива
Тогда можно сказать следующее: A) Функция Ляпунова положительная знакоопределенная функцияD) Производная функции Ляпунова положительная знакоопределенная функция H) Функция Ляпунова положительная знакоопределенная, а ее производная положительная знакопостоянная функция, поэтому система неустойчива
При исследовании устойчивости нелинейной системы функция Ляпунова  Тогда можно сказать следующее: A) Функция Ляпунова положительная знакоопределенная функцияF) Производная функции Ляпунова положительная знакопостоянная функция G) Функция Ляпунова положительная знакоопределенная, а ее производная отрицательная знакопостоянная функция, поэтому система устойчива
Тогда можно сказать следующее: A) Функция Ляпунова положительная знакоопределенная функцияF) Производная функции Ляпунова положительная знакопостоянная функция G) Функция Ляпунова положительная знакоопределенная, а ее производная отрицательная знакопостоянная функция, поэтому система устойчива
При исследовании устойчивости нелинейной системы функция Ляпунова  , Тогда можно сказать следующее:A) Функция Ляпунова положительная знакоопределенная функция E) Производная функции Ляпунова отрицательная знакоопределенная функция G) Функция Ляпунова положительная знакоопределенная, а ее производная отрицательная знакоопределенная функция, поэтому система асимптотически устойчива
, Тогда можно сказать следующее:A) Функция Ляпунова положительная знакоопределенная функция E) Производная функции Ляпунова отрицательная знакоопределенная функция G) Функция Ляпунова положительная знакоопределенная, а ее производная отрицательная знакоопределенная функция, поэтому система асимптотически устойчива
При исследовании устойчивости нелинейной системы функция Ляпунова 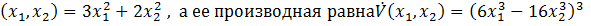 Тогда можно сказать следующее:A) Функция Ляпунова положительная знакоопределенная функция F) Производная функции Ляпунова знакопеременная функция H) Функция Ляпунова положительная знакоопределенная, а ее производная знакопеременная функция, поэтому мы не можем определить система устойчива или неустойчива
Тогда можно сказать следующее:A) Функция Ляпунова положительная знакоопределенная функция F) Производная функции Ляпунова знакопеременная функция H) Функция Ляпунова положительная знакоопределенная, а ее производная знакопеременная функция, поэтому мы не можем определить система устойчива или неустойчива
При исследовании устойчивости нелинейной системы функция Ляпунова  Тогда можно сказать следующее:A) Функция Ляпунова положительная знакоопределенная функция D) Производная функции Ляпунова положительная знакопостоянная функция H) Функция Ляпунова положительная знакоопределенная, а ее производная положительная знакопостоянная функция, поэтому система неустойчива
Тогда можно сказать следующее:A) Функция Ляпунова положительная знакоопределенная функция D) Производная функции Ляпунова положительная знакопостоянная функция H) Функция Ляпунова положительная знакоопределенная, а ее производная положительная знакопостоянная функция, поэтому система неустойчива
При исследовании устойчивости нелинейной системы функция Ляпунова 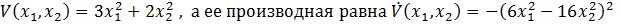 Тогда можно сказать следующее: A) Функция Ляпунова положительная знакоопределенная функция E) Производная функции Ляпунова отрицательная знакопостоянная функция G) Функция Ляпунова положительная знакоопределенная, а ее производная отрицательная знакопостоянная функция, поэтому система устойчива
Тогда можно сказать следующее: A) Функция Ляпунова положительная знакоопределенная функция E) Производная функции Ляпунова отрицательная знакопостоянная функция G) Функция Ляпунова положительная знакоопределенная, а ее производная отрицательная знакопостоянная функция, поэтому система устойчива
При исследовании устойчивости нелинейной системы функция Ляпунова 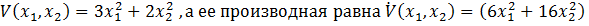 Тогда можно сказать следующее:A) Функция Ляпунова положительная знакоопределенная функция D) Производная функции Ляпунова положительная знакоопределенная функция H) Функция Ляпунова положительная знакоопределенная, а ее производная положительная знакоопределенная функция, поэтому система неустойчива
Тогда можно сказать следующее:A) Функция Ляпунова положительная знакоопределенная функция D) Производная функции Ляпунова положительная знакоопределенная функция H) Функция Ляпунова положительная знакоопределенная, а ее производная положительная знакоопределенная функция, поэтому система неустойчива
При исследовании устойчивости нелинейной системы функция Ляпунова  Тогда можно сказать следующее: A) Функция Ляпунова положительная знакоопределенная функция E) Производная функции Ляпунова отрицательная знакоо
Тогда можно сказать следующее: A) Функция Ляпунова положительная знакоопределенная функция E) Производная функции Ляпунова отрицательная знакоо
|
из
5.00
|
Обсуждение в статье: Теория нелинейных систем автоматического управления_каз |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

