 |
Главная |
Нормальное уравнение плоскости в координатной форме
|
из
5.00
|
Приведем общее уравнение плоскости Ax + By + Cz + D = 0 (*) к нормальному виду. Рассмотрим векторы 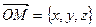 и
и 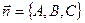 . Тогда (*) можно записать в векторной форме:
. Тогда (*) можно записать в векторной форме:
 (**).
(**).
Разделим обе части уравнения на n: 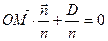 или
или
 (9').
(9').
Возможны два случая.
1. D<0. Чтобы (9') совпало с (9), уравнение (**) делим на  .
.
2. D>0. В этом случая делим на  (
(  ).
).
Т.о., чтобы уравнение (8) привести к нормальному виду, надо умножить на нормирующий множитель  , знак которого выбирается противоположным знаку D:
, знак которого выбирается противоположным знаку D:  .
.
Пример. Привести к нормальному виду: x – 2y + 2z + 12 = 0.
Т.к. D=12>0, то м<0:  ,
, 
 ;
;  ,
,  ,
,  ,
, 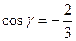 .
.
Отклонение и расстояние от точки до плоскости.
 Пусть дана точка М0(x0, y0, z0) и плоскость
Пусть дана точка М0(x0, y0, z0) и плоскость  . Найдем расстояние от точки до данной плоскости.
. Найдем расстояние от точки до данной плоскости.
1. Пусть точки О и М0 лежат по разные стороны данной плоскости. Через точку М0 проведем плоскость, параллельную данной.
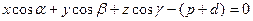 (*)
(*)
Точка М0 лежит на этой плоскости, поэтому
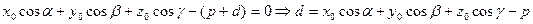
2. Если т. М0 и т. О0 находятся по одну сторону плоскости, то в (*) свободный член будет (p – d) и
 . Поэтому общая формула:
. Поэтому общая формула:
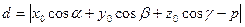 ,
, 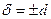 .
.
Отклонением д точки М0 от плоскости называется расстояние d, если точка М0 и начало координат лежат по разные стороны плоскости и (-d), если они лежат по одну сторону плоскости.
Пример. Найти расстояние от точки М0(-2, -4, 3) до плоскости 2x – y + 2z + 3 = 0. Приводим уравнение к нормальному виду и подставляем координаты точки:
 ,
, 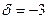 ,
,  .
.
Точка М0 и точка О лежат по одну сторону плоскости (д<0).
Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей.
 Пусть даны две плоскости:
Пусть даны две плоскости:  . Нормальные векторы их:
. Нормальные векторы их:  и
и  . Тогда
. Тогда  или
или 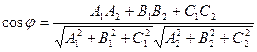 . Если плоскости перпендикулярны, то
. Если плоскости перпендикулярны, то  и А1А2 + В1В2 + С1С2 = 0,
и А1А2 + В1В2 + С1С2 = 0, 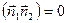 - условие перпендикулярности.
- условие перпендикулярности.
Если плоскости параллельны, то  и
и  , т.е. они коллинеарны.
, т.е. они коллинеарны.
Условие параллельности плоскостей в координатной форме:
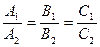 .
.
Пример 1. Определить угол между плоскостями: 3x + 2y – 2z =0 и x + 2y + 6z – 12 = 0.
 .
.
Пример 2. Определить при каких значениях l и m уравнения mx + 3y – 2z – 1 =0 и 2x – 5y – lz = 0 определяют параллельные плоскости.
 ,
,  ,
,  .
.
Пример 3. Через точку М0(1, -3, -2) провести плоскость, параллельную данной: 2x – 3y + 4z – 2 = 0.
A(x – x0) + B(y – y0) + C(z – z0) = 0, A(x – 1) + B(y + 3) + C(z + 2) = 0
 , A = 2k, B = -3k, C = 4k (k=1)
, A = 2k, B = -3k, C = 4k (k=1)
 , 2x – 3y + 4z – 3 = 0.
, 2x – 3y + 4z – 3 = 0.
Задание линии в пространстве.
 Линию L в пространстве можно задать как пересечение двух поверхностей. Пусть точка M(x, y, z), лежащая на линии L, принадлежит как поверхности Р1, так и поверхности Р2. Тогда координаты этой точки должны удовлетворять уравнениям обеих поверхностей. Поэтому под уравнением линии L в пространстве понимают совокупность двух уравнений, каждое из которых является уравнением соответствующей поверхности:
Линию L в пространстве можно задать как пересечение двух поверхностей. Пусть точка M(x, y, z), лежащая на линии L, принадлежит как поверхности Р1, так и поверхности Р2. Тогда координаты этой точки должны удовлетворять уравнениям обеих поверхностей. Поэтому под уравнением линии L в пространстве понимают совокупность двух уравнений, каждое из которых является уравнением соответствующей поверхности:

Линии L принадлежат те и только те точки, координаты которых удовлетворяют обоим уравнениям в (*). Позже мы рассмотрим и другие способы задания линий в пространстве.
Пример.

 - уравнение оси OZ.
- уравнение оси OZ.
|
из
5.00
|
Обсуждение в статье: Нормальное уравнение плоскости в координатной форме |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

