 |
Главная |
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
|
из
5.00
|
Задачи по определению температурного поля решаются на основании дифференциального уравнения теплопроводности, выводы которого даны в специальной литературе. Ниже приводятся варианты дифференциальных уравнений без выводов.
При решении задач теплопроводности в движущихся жидкостях, характеризующих нестационарное трехмерное температурное поле с внутренними источниками теплоты, используется уравнение

Выражение (2.10) является дифференциальным уравнением энергии в декартовой системе координат (уравнение Фурье - Кирхгофа). В этом виде оно применяется при изучении процесса теплопроводности в любых телах.
При 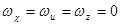 , т.е. когда рассматривается твердое
, т.е. когда рассматривается твердое
тело без внутренних источников теплоты (  = 0), уравнение энергии (2.10) переходит в уравнение теплопроводности для твердых тел (уравнение Фурье):
= 0), уравнение энергии (2.10) переходит в уравнение теплопроводности для твердых тел (уравнение Фурье):

Величину  =а (м2/с) в уравнении (2.10) называют коэффициентом температуропроводности, который является физическим параметром вещества, характеризующим скорость изменения температуры в теле при неустановившихся процессах.
=а (м2/с) в уравнении (2.10) называют коэффициентом температуропроводности, который является физическим параметром вещества, характеризующим скорость изменения температуры в теле при неустановившихся процессах.
Если коэффициент теплопроводности характеризует способность тел проводить теплоту, то коэффициент температуропроводности является мерой теплоинерционных свойств тела. Из уравнения (2.10) следует, что изменение температуры во времени  для любой точки пространства пропорционально величине а, т.е. скорость изменения температуры в любой точке тела будет тем выше, чем больше коэффициент температуропроводности. Поэтому при прочих равных условиях выравнивание температур во всех точках пространства будет происходить быстрее в том теле, которое обладает большим коэффициентом температуропроводности. Коэффициент температуропроводности зависит от природы вещества. Например, жидкости и газы обладают большой тепловой инерционностью и, следовательно, малым коэффициентом температуропроводности. Металлы имеют малую тепловую инерционность, так как характеризуются большим коэффициентом температуропроводности.
для любой точки пространства пропорционально величине а, т.е. скорость изменения температуры в любой точке тела будет тем выше, чем больше коэффициент температуропроводности. Поэтому при прочих равных условиях выравнивание температур во всех точках пространства будет происходить быстрее в том теле, которое обладает большим коэффициентом температуропроводности. Коэффициент температуропроводности зависит от природы вещества. Например, жидкости и газы обладают большой тепловой инерционностью и, следовательно, малым коэффициентом температуропроводности. Металлы имеют малую тепловую инерционность, так как характеризуются большим коэффициентом температуропроводности.
Для обозначения суммы вторых производных по координатам в уравнениях (2.10) и (2.11) можно использовать символ 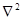 - называемый оператор Лапласа. Тогда в декартовой системе координат
- называемый оператор Лапласа. Тогда в декартовой системе координат

Выражение 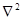 t в цилиндрической системе координат имеет вид
t в цилиндрической системе координат имеет вид
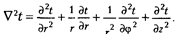
Для твердого тела в стационарных условиях с внутреннимисточником теплоты уравнение (2.10) преобразуется в уравнение Пуассона:

Наконец, для стационарной теплопроводности и при отсутствии внутренних источников теплоты уравнение (2.10) принимает вид уравнения Лапласа:

Дифференциальное уравнение теплопроводности в цилиндрических координатах с внутренним источником теплоты
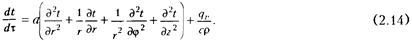
2.1.6. УСЛОВИЯ ОДНОЗНАЧНОСТИ ДЛЯ
ПРОЦЕССОВ ТЕПЛОПРОВОДНОСТИ
Так как дифференциальное уравнение теплопроводности выведено на основе общих законов физики, то оно характеризует явление теплопроводности в самом общем виде. Поэтому можно сказать, что приведенные дифференциальные уравнения характеризуют целый класс явлений теплопроводности. Чтобы из бесчисленного количества выделить конкретно рассматриваемый процесс и дать его полное математическое описание, к дифференциальному уравнению необходимо присоединить математическое описание всех частных особенностей рассматриваемого процесса. Эти частные особенности, которые совместно с дифференциальным уравнением дают полное математическое описание конкретного процесса теплопроводности, называются условиями однозначности или краевыми условиями и включают в себя:
а) геометрические условия, характеризующие форму и размеры тела, в которых протекает процесс;
б) физические условия, характеризующие физические свойства среды и тела ( 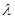 ,
, 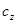 ,
,  ,а и др.);
,а и др.);
в) временные (начальные) условия, характеризующие распределение температур в изучаемом теле в начальный момент времени;
г) граничные условия, характеризующие взаимодействие рассматриваемого тела с окружающей средой.
Начальные условия необходимы при рассмотрении нестационарных процессов и состоят в задании закона распределения температуры внутри тела в начальный момент времени. В общем случае начальное условие аналитически может быть записано следующим образом: при 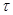 = О
= О

В случае равномерного распределения температуры в теле начальное условие упрощается: при 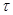 = 0 t = t
= 0 t = t  = idem.
= idem.
Граничные условия могут быть заданы несколькими способами.
1. Граничные условия первого рода, задающие распределение температуры на поверхности тела t  для каждого момента времени:
для каждого момента времени:

В частном случае, когда температура на поверхности постоянна на протяжении всего времени протекания процессов теплообмена, уравнение (2.16) упрощается и принимает вид t  = idem.
= idem.
2. Граничные условия второго рода, задающие величину плотности теплового потока для каждой точки поверхности и любого момента времени. Аналитически это можно представить следующим образом:

где q - плотность теплового потока на поверхности тела.
В простейшем случае плотность теплового потока по поверхности и во времени остается постоянной: q = idem. Такой случай теплообмена имеет место, например, при нагревании различных металлических изделий в высокотемпературных печах.
3. Граничные условия третьего рода, задающие температуру окружающей среды  и закон теплообмена между поверхностью тела и окружающей средой. Для описания процесса теплообмена между поверхностью тела и средой используется закон Ньютона.
и закон теплообмена между поверхностью тела и окружающей средой. Для описания процесса теплообмена между поверхностью тела и средой используется закон Ньютона.
Согласно закону Ньютона количество теплоты, отдаваемое единицей поверхности тела в единицу времени, пропорционально разности температур тела t  и окружающей среды
и окружающей среды  :
:

Коэффициент теплоотдачи характеризует интенсивность теплообмена между поверхностью тела и окружающей средой.
Численно он равен количеству теплоты, отдаваемому (или воспринимаемому) единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой, равной одному градусу.
Согласно закону сохранения энергии количество теплоты, которое отводится с единицы поверхности в единицу времени вследствие теплоотдачи (2.18), должно равняться теплоте, подводимой к единице поверхности в единицу времени вследствие теплопроводности из внутренних объемов тела (2.7):

где п - нормаль к поверхности тела; индекс "с" указывает, что температура и градиент относятся к поверхности тела (при п = 0).
Окончательное граничное условие третьего рода можно записать в следующем виде:

Уравнение (2.20) по существу является частным выражением закона сохранения энергии для поверхности тела.
4. Граничные условия четвертого рода, характеризующие условия теплообмена системы тел или тела с окружающей средой по закону теплопроводности. Предполагается, что между телами осуществляется идеальный контакт (температуры соприкасающихся поверхностей одинаковы). В рассматриваемых условиях имеет место равенство тепловых потоков, проходящих через поверхность соприкосновения:

|
из
5.00
|
Обсуждение в статье: ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

