 |
Главная |
Напряжений и деформаций
|
из
5.00
|
Следует различать два вида концентрации напряжений в сварных соединениях, которые могут быть использованы в расчетах.
1. Концентрация напряжений, вызываемая формой шва.
2. Концентрация напряжений, вызываемая видом соединения и формой детали (имеется в виду концентрация погонных нагрузок, передаваемых отдельными участками шва, например, в случае фланговых швов).
Опыт показывает, что одновременное определение двух видов коэффициентов концентрации требует огромного числа предварительных экспериментов, а расчет с применением ЭВМ по методу конечных элементов в отношении сварных соединений делает эту задачу недоступной даже с использованием вычислительных машин.
Коэффициент концентрации напряжений может быть определен по формуле:

где smax- максимальное напряжение; scp- средние напряжения.
Помимо концентрации напряжений также может иметь место концентрация деформаций, которая характеризуется коэффициентом

При расчетах на статические нагрузки as, ae в явном виде не входят, т.к. инженерный метод исходит из модели абсолютно жесткого твердого тела. При переменных нагрузках расчет тот же, что и при статических, но вводятся новые коэффициенты запаса. Однако не учитывается тот факт, что предел выносливости сильно зависит от концентрации напряжений.
Для выполнения более достоверных расчетов необходимо пользоваться методами, включающими податливость материала, его упругость и даже пластическое течение.
В настоящее время существуют два принципиальных подхода к оценю влияния концентрации напряжений:
а) метод, учитывающий концентрацию напряжений as и радиус концентратора (r), причем радиус (r) является одним из существенных факторов;
б) аппарат линейной механики разрушения, который исходит из того, что в концентраторах (трещинах) r®0.
Рассмотрим нагружение пластины с надрезами (рисунок 2.11).
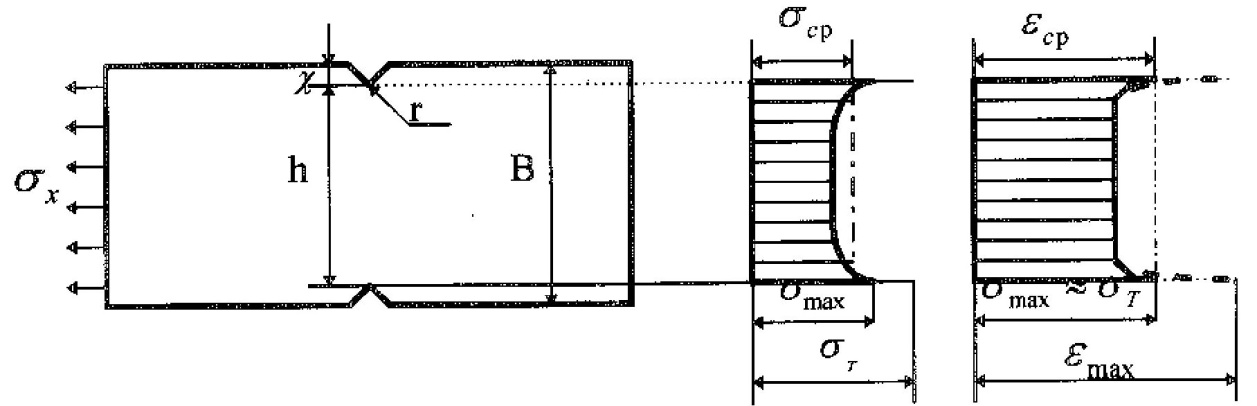
Рисунок 2.11 – Напряжения и деформации в пластине с надрезами
Когда напряжение smax достигает sT, у вершины концентратора начинает появляться пластическая деформация, в результате чего коэффициент концентрации напряжений as будет уменьшаться.
Но поскольку пластическая деформация происходит неравномерно и сосредоточена на локальных участках (у надреза), коэффициент концентрации деформаций ae будет расти. Существуют понятия мелкого и глубокого надрезов, которые используются в обоих подходах.
Мелкий надрез, когда h>>t и изменение h при постоянном t мало влияет на коэффициент концентрации напряжений:

Глубокий надрез - когда h<t и as зависит от изменения h и практически не зависит от t:

где А и Д - постоянные коэффициенты.
Ввиду того, что при r®0, as®¥, а фактическое поведение металла в плане прочности перестает зависеть от as, то взамен коэффициента концентрации напряжений в линейной механике разрушения применяется коэффициент интенсивности напряжений К.
В общем виде
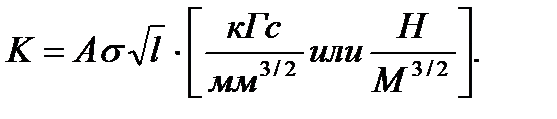
Критерий К применим при r®0 (для трещин), кроме того для трещин с углом раскрытия j=0 (рисунок 2.12).
Строго говоря, у вершины трещин почти всегда возникает хотя бы небольшая зона пластических деформаций, но применительно к трещиноподобным дефектам можно пользоваться линейной механикой разрушения пока эти зоны малы по сравнению с размером трещины и толщиной металла.
Более универсальным критерием является критерий G (энергия, затраченная на работу по увеличению длины трещины) в виду того, что он может обслуживать и концентраторы с углом раскрытия надреза (трещины) неравном нулю (j¹0) (рисунок 2.13).

Рисунок 2.12 – Применимость критерия К

Рисунок 2.13 – Поведение критерия G1 в начале движения трещины
В момент начала движения трещины длиной l с места (увеличения длины трещины на Dl) при j ¹ 0, значение G быстро возрастает от 0 до G1, соответствующего значению критерия при плоской деформации (j = 0).
С энергетической точки зрения острые концентраторы (r»0) с углами j£30-45° при подрастании от их вершин трещин ведут себя почти как трещины.
Между механическими и энергетическими критериями существует тесная взаимосвязь. Для трещин при угле раскрытия равном нулю(j=0) и плоского напряженного состояния

При плоском деформированном состоянии (объемном напряженном)

где Е - модуль упругости, m - коэффициент Пуассона.
Также для описания напряженно-деформированного состояния применяется коэффициент интенсивности деформаций V. При угле раскрытия дефекта равном нулю:
V = εmax √r = εср αε √r.
Значение  слабо зависит от величины r , т.к. в случае параллельных граней надреза коэффициент концентрации
слабо зависит от величины r , т.к. в случае параллельных граней надреза коэффициент концентрации  .
.
При радиусе в вершине концентратора r=0 (трещина) значение V с точностью до постоянного коэффициента совпадает с К.

По аналогии с законом Гука:
 s=Еe.
s=Еe.
2.4. Характеристики сопротивляемости металла разрушению в присутствии концентраторов
Традиционным приемом оценки механических свойств металла является нагружение образца или детали до разрушения с регистрацией в процессе испытаний и (или) после него каких-либо характеристик напряженно-деформированного состояния, например, при растяжении стандартных гладкие образцов - предела текучести sT(s0,2), временного сопротивления sB, относительного удлинения и т.д. Существует несколько различных способов определения деформированного состояния и методов испытаний, которые с различной степенью достоверности позволяют делать выводы о работоспособности деталей и конструкций.
|
из
5.00
|
Обсуждение в статье: Напряжений и деформаций |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

