 |
Главная |
Список использованных обозначений
|
из
5.00
|
А.И. Кобрунов
Математические основы теории интерпретации геофизических данных.
Ухта 2007
УДК 550 830
Кобрунов А.И. Математические основы теории интерпретации геофизических данных. Учебное пособие, - Ухта: УГТУ, 2007. - с.: ил.
ISSN
Учебное пособие является междисциплинарным в том отношении, что обеспечивает углубленное изучение целого ряда дисциплин, при подготовке бакалавров, специалистов, магистров и аспирантов. Оно обеспечивает изучение дисциплин «Теоретические основы решения обратных задач геофизики», «Теоретические основы обработки геофизической информации», углубленное изучение интерпретационных разделов геофизических спецкурсов и, прежде всего, «Гравиразведка», «Магниторазведка», «Комплексная интерпретация», а также разделов, связанных с современным математическим аппаратом геофизики. Приложения к учебному пособию будут полезны при изучении математического цикла дисциплин при подготовке геофизиков.
Учебное пособие предназначено для студентов, магистрантов и аспирантов, обучающихся по специальностям 130201 «Геофизические методы поисков и разведки месторождений полезных ископаемых» и 130202 «Геофизические методы исследования скважин», специализирующихся на вопросах теории интерпретации геофизических данных. Предполагается его активное использование при подготовке курсовых, дипломных работ, а также магистерских диссертаций по программе 130121 «Автоматизированные методы обработки и интерпретации геолого-геофизической информации». Оно будет полезно при подготовке аспирантов по специальностям 25.00.10 «Геофизика, геофизические методы поисков полезных ископаемых», 25.00.16 «Горнопромышленная и нефтегазопромысловая геология, геофизика, маркшейдерское дело и геометрия недр» и 05.13.18 «Математическое моделирование, численные методы и комплексы программ» с приложениями в области геофизики.
В учебном пособии рассмотрены информационные и интерпретационные модели анализа геофизических данных, математические постановки задач, обеспечивающих разные информационные уровни интерпретационного процесса в геофизике а также принципы и методы их решения. Рассматриваются методы решения некорректных задач геофизики в условиях максимально полного учета особенностей и специфики геофизических задач и геофизических данных. Более подробно изложены современная теория и методы построения сложных плотностных моделей геологических сред с использованием гравиметрических данных.
Рецензенты: зав. кафедрой разведочной геофизики и компьютерных систем РГУНГ им. И.М. Губкина, доктор технических наук, профессор Серкеров С.А.; зав. кафедрой ядерно-радиометрических методов и геоинформатики МГГРУ, доктор физ. – мат. наук, профессор Никитин А.А.
Редактор
Имей мужество пользоваться
собственнымумом!
Эммануил Кант.
Предисловие.
Девиз, вынесенный в эпиграф отражает стиль учебного пособия, направленного, прежде всего на решение задачи геофизического просвещения. Но что это такое? Следуя Иммануилу Канту - немецкому философу XVIII в. - просвещение — это выход человека из состояния несовершеннолетия, в котором он находится по собственной вине. Несовершеннолетие — это неспособность пользоваться своим рассудком без руководства со стороны кого-то другого. Несовершеннолетие по собственной вине имеет причиной не недостаток рассудка, а недостаток мужества пользоваться им без руководства со стороны кого-то другого. Геофизическое просвещение – типичный пример такого свойства просвещения. Это привитие умения не просто следовать рекомендованным технологиям, приемам и способам, а выработка мужества пользоваться собственным умом в оценке и конструировании методов и технологий. В данном случае – методов и технологий извлечения информации из геофизических данных.
Учебное пособие предназначено для студентов, магистрантов и аспирантов, обучающихся по специальностям геофизические методы поисков и разведки месторождений полезных ископаемых, и геофизические методы исследования скважин, специализирующихся на вопросах теории интерпретации геофизических данных. Оно будет полезно также инженерам геофизикам и научным работникам как краткий обзор математических моделей и постановок задач извлечения информации из геофизических данных. Спецификой материала, собранного в учебном пособии является рассмотрение недоопределенных обратных задач геофизики и связанных с этим особенностей. Акцент делается не на вычислительных и технологических проблемах, связанных с решением соответствующих уравнений, а прежде всего, на смысловых, содержательных вопросах. Важнейший из них состоит в выработке постановки обратных задач адекватной задачам геолого – геофизической интерпретации, смыслу, содержанию и форме реально имеющейся информации об изучаемом объекте. Другой особенностью учебного пособия служит возможность его использования как своего рода трамплина для самостоятельных научных исследований. Читатель вплотную подводится к «грани изученного». Это делает пособие полезным для аспирантов не только геофизических специальностей но и специальности «прикладная математика и математическое моделирование», выбравших в качестве приложения геофизические методы. В настоящее время уровень развития стандартных и специализированных общедоступных математических библиотек таков, что решить практически любую из реально возникающих обратных задач на уже достигнутых вычислительных мощностях не составляет существенных проблем. Дальнейшее наращивание вычислительных мощностей и развитие программного обеспечения будет делать эту задачу все более рутинной и просто реализуемой. В этой связи акцент в изучении методов интерпретации должен быть сделан на глубоком осмыслении постановок обратных задач, их системной организации, встраивании процедур анализа полей в интегрированные методы комплексной интерпретации, в том числе и с использованием информации о генезисе изучаемых объектов. Настоящее учебное пособие посвящено указанным вопросам и призвано восполнить имеющийся сегодня пробел в учебной литературе по математическим основам теории интерпретации геофизических данных.
Специфика рассматриваемого предмета такова, что она требует активного и постоянного использования математической символики, математических понятий и методов. Следует помнить, что язык математики, это прежде всего язык. Язык, позволяющий недвусмысленно и точно выражать свои мысли. Нет другого способа точно сказать о том, что задано, как установлены связи и что следует найти. Здесь то, чаще всего и скрыта основная трудность. Недостаточный объем математической подготовки, отсутствие в учебных планах важнейших разделов математики, на которых «стоит» теория и методы решения обратных задач – основы математической теории интерпретации, приводит к существенным трудностям. Студенты готовы очень внимательно слушать о принципах интегрированного анализа геолого – гофизических данных, о совместной интерпретации сейсмо-гравиметрических материалов на основе решения обратных задач. Но как только дело доходит до записи волновых уравнений для неоднородных сред и краевых задач для уравнений эллиптического типа, дело двигается тяжелее. Но есть и еще одна проблема – если можно выразиться – проблема второго этажа. Она касается уже не боящихся математической символики аспирантов, студентов и магистрантов. Модные и доступные вычислительные приемы, позволяющие быстро и просто провести преобразование над полем создают, в купе с красивыми средствами визуализации, иллюзию простоты решаемой задачи. Например, выполнив вейвлет преобразование или красиво звучащую, например «адаптивную в живом окне», фильтрацию получим распределение источников поля или, на худой конец распределение его эффективных параметров. Далее этот результат передается «на вход» геологического осмысления и строятся просто сногосшибающие выводы. Но есть фундаментальные результаты более глубокого этажа характеризующие эффекты неединственности и доказывающие бесполезность таких простых решений. Шапочное владение новыми информационными и компью.терными технологиями не отменяет действие фундаментальных законов извлечения информации из физических полей. Их надо знать. К сожаленю в учебной литературе они отражены крайне слабо и сама эта литература уже стала библиографической редкостью. Настоящее учебное пособие нацелено, в том числе и на эту проблематику.
Теперь о том, как следует читать настоящее пособие. Если читатель считает, что он достаточно владеет математическим аппаратом, ему следует убедиться в этом, просмотрев приложения 1-2, и приступить к чтению собственно разделов основной части. В противном случае, рекомендую после того как будет проработано введение, прочитать приложение 1. После этого смело можно читать главы 1 и 2. Перед главой 3 следует прочитать приложение 2, возможно опуская те его части, которые помечены звездочкой. Они приведены для полноты и носят «внутренний характер». Это значить, что они нужны для более четкой формулировки других утверждений, которые уже активно используются. Особо важны разделы - линейные операторы, дифференцирование. Перед чтением главы 5 следует вернуться к приложению 2 и внимательно еще раз вспомнить вопросы теории оптимизации – раздел «Экстремальные задачи». Перед чтением главы 6 следует ознакомиться с приложением 3. Что же касается приложения 4 – это самостоятельный раздел, не используемый в основной части и направленный на «приглашение к сотрудничеству». Он направлен на развитие идей связанных с построением эффективных моделей и может служить основой для выполнения самостоятельных научных исследований. Это хорошая тема длдя выполнения курсовых, дипломных работ, подготовки магистрских диссертаций.
Список использованных обозначений
Все обозначения определяются там, где они впервые используются. Однако для удобства наведения справок ниже приводится их основная сводка. Определение понятий в тексте помечено курсивом.
В каждом разделе геофизики и математической физики при введении обозначений есть свои традиции. В теории упругости  обозначают упругую константу, в электрометрии – проводимость а в гравиметрии – плотность. Ту же плотность в теории распространения волн обозначают
обозначают упругую константу, в электрометрии – проводимость а в гравиметрии – плотность. Ту же плотность в теории распространения волн обозначают  , а скорость – символом
, а скорость – символом 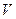 . Но этим символом обозначают и область определения функции пространственных переменных также как и сами пространственные переменные обозначают перечнем координат, символами с и индексами и просто буквой
. Но этим символом обозначают и область определения функции пространственных переменных также как и сами пространственные переменные обозначают перечнем координат, символами с и индексами и просто буквой  . Поскольку в этом пособии собраны сведения из различных разделов и предполагается, что читатель более подробные сведения будет получать из специальной литературы, где сильны упоминавшиеся специфические традиции в обозначениях, мы их по возможности придерживаемся. При этом каждый раз, где это может привести к разночтениям, оговариваемпозволяет избежать путаницы.
. Поскольку в этом пособии собраны сведения из различных разделов и предполагается, что читатель более подробные сведения будет получать из специальной литературы, где сильны упоминавшиеся специфические традиции в обозначениях, мы их по возможности придерживаемся. При этом каждый раз, где это может привести к разночтениям, оговариваемпозволяет избежать путаницы.
Пространственные координаты чаще всего обозначаются символами  либо
либо  . Для обозначения всей совокупности пространственных переменных используется либо символ v, либо
. Для обозначения всей совокупности пространственных переменных используется либо символ v, либо  , либо
, либо 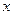 . Все определяется текущими потребностями, удобствами письма и каждый раз оговаривается. Для времени используются обозначение
. Все определяется текущими потребностями, удобствами письма и каждый раз оговаривается. Для времени используются обозначение 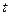 либо
либо 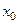 .
.
γ – гравитационная постоянная = 6,674•10-11м3/кг•с2 ;
 – принадлежит;
– принадлежит;
 – не принадлежит;
– не принадлежит;
 - пересечение;
- пересечение;
 - пересечение множеств Bi , i=1+n;
- пересечение множеств Bi , i=1+n;
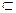 - включение;
- включение;
/ - дополнение;
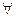 - квантор всеобщности;
- квантор всеобщности;
 - квантор существования;
- квантор существования;
 – замыкание множества
– замыкание множества 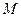 (если не оговорено противное);
(если не оговорено противное);
 – множество значений отображения A;
– множество значений отображения A;
A(N) – образ множества N при отображении A;
DA – область определения отображения A;
 – ядро отображения A: (
– ядро отображения A: (  ={
={  }) ;
}) ;
 - класс эквивалентности для отображения A;
- класс эквивалентности для отображения A;
 - производная Фреше оператора
- производная Фреше оператора  в точке
в точке 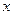 ;
;
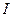 - единичный оператор. Иногда используется запись
- единичный оператор. Иногда используется запись  . В последнем случае это связано с традициями обозначений в теории матрицю;
. В последнем случае это связано с традициями обозначений в теории матрицю;
 – прямая сумма;
– прямая сумма;
 –верхняя грань значений выражения
–верхняя грань значений выражения 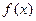 по всем
по всем 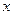 принадлежащим множеству
принадлежащим множеству 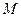 ;
;
 - существенная верхняя грань (верхняя грань по множеству
- существенная верхняя грань (верхняя грань по множеству 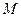 за исключением подмножества меры нуль);
за исключением подмножества меры нуль);
 –нижняя грань значений выражения
–нижняя грань значений выражения 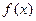 по всем
по всем 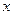 принадлежащим множеству
принадлежащим множеству 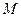 ;
;
 - сопряженное к
- сопряженное к 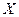 пространство;
пространство;
 - значение линейного ограниченного функционала, определяемого элементом
- значение линейного ограниченного функционала, определяемого элементом 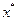 из двойственного к
из двойственного к 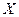 пространства наэлементе
пространства наэлементе 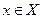 ;
;
 - скалярное произведение векторов
- скалярное произведение векторов  и
и  ;
;
 - векторное произведение векторов
- векторное произведение векторов  и
и  ;
;
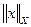 – норма элемента
– норма элемента 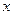 в пространстве X;
в пространстве X;
N┴ - аннулятор множества N (ортогональное дополнение в случае гильбертова пространства);
[X→Y] – множество линейных замкнутых операторов из X в Y;
A* - оператор, сопряженный к A;
A-1 – обратный к A оператор;
 - модуль непрерывности оператора
- модуль непрерывности оператора 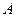 , действующего из
, действующего из  в Y ;
в Y ;
 - модуль непрерывности обратного оператора к A в норме пространств X, Y на множестве M;
- модуль непрерывности обратного оператора к A в норме пространств X, Y на множестве M;
 – гильбертово пространство функций
– гильбертово пространство функций  пространственная переменная) с нормой;
пространственная переменная) с нормой;
 ;
;
 – множество неперерывных в V функций с нормой:
– множество неперерывных в V функций с нормой:
 ;
;
 – множество функций в V, непрерывных вместе со всеми своими частными производными до порядка r и с конечной нормой, определенной соотношением:
– множество функций в V, непрерывных вместе со всеми своими частными производными до порядка r и с конечной нормой, определенной соотношением:
 ;
;
 - суммирование по всевозможным комбинациям индексов k таких, что: k1, k2, k3≥0; k1+k2+k3=k;
- суммирование по всевозможным комбинациям индексов k таких, что: k1, k2, k3≥0; k1+k2+k3=k;
 - множество бесконечно дифференцируемых и непрерыывных вместе со всеми своими производными функций, равных нулю, на границе области V;
- множество бесконечно дифференцируемых и непрерыывных вместе со всеми своими производными функций, равных нулю, на границе области V;
 – множество функций в V с конечной нормой:
– множество функций в V с конечной нормой:
 ;
;
 ;
;
 ;
;
 - норма оператора A, действующего из Lp в Lq;
- норма оператора A, действующего из Lp в Lq;
X\M – фактор-пространство пространства X по подпространству M;
[X] – классы смежности (элементы фактор-пространства);
sign – функция знака:

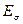 - разложение единицы оператора A;
- разложение единицы оператора A;
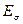 представляет собой для каждого значения параметра
представляет собой для каждого значения параметра  , оператор проектирования на подпространство, образованное из собственных функций, соответствующих собственным значениям, не превосходящим величины
, оператор проектирования на подпространство, образованное из собственных функций, соответствующих собственным значениям, не превосходящим величины  . Если A – линейный, ограниченный, самосопряженный и положительный оператор, то:
. Если A – линейный, ограниченный, самосопряженный и положительный оператор, то:
 ;
;
Wr(v) – соболевское пространствообразованное пополнением  по норме:
по норме:
 ;
;
 - множество числовых последовательностей длины n с нормой:
- множество числовых последовательностей длины n с нормой:

 множество последовательностей
множество последовательностей  из бесконечного числа элементов, сходящихся относительно нормы
из бесконечного числа элементов, сходящихся относительно нормы

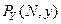 - операция проектирования элемента
- операция проектирования элемента  на множество
на множество  в норме пространства
в норме пространства  ;
;
 - то же, что и
- то же, что и 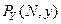 при ясном из контекста виде пространства
при ясном из контекста виде пространства  ;
;
 - образ множества
- образ множества 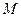 при проектировании на множество
при проектировании на множество  в норме пространства
в норме пространства 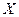 ;
;
 - то же что и
- то же что и  при ясном из контекста виде пространства
при ясном из контекста виде пространства 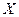 ;
;
 оператор проектирования функции
оператор проектирования функции  имеющей носитель
имеющей носитель  на функцию с носителем
на функцию с носителем  ;
;
mes(V) – мера множества V (площадь, объем) ;
E_ - область нижнего полупространства (z>0);
E0 – горизонтальная плоскость z=0;
E+ - верхнее полупространство (z<0);
П – горизонтальная полоса в E_;
 – экстремальный класс. Символ используется для обозначения полных или идеальных экстремальных классов;
– экстремальный класс. Символ используется для обозначения полных или идеальных экстремальных классов;
 – почти идеальный экстремальный класс;
– почти идеальный экстремальный класс;
 – идеальные экстремальные классы распределения плотности ;
– идеальные экстремальные классы распределения плотности ;
 – почти идеальные экстремальные классы распределения плотности ;
– почти идеальные экстремальные классы распределения плотности ;
 - экстремальные классы для плотностных границ;
- экстремальные классы для плотностных границ;
 – характеристическая функция множества M :
– характеристическая функция множества M :

 - прямое преобразование Фурье функции
- прямое преобразование Фурье функции  по переменным x,y;
по переменным x,y;
 - обратное преобразование Фурье функции
- обратное преобразование Фурье функции  по переменным
по переменным  .
.
Если функция  зависит от координат
зависит от координат  то для
то для  используется сокращенная запись
используется сокращенная запись 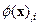 .
.
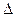 - оператора Лапласа, имеющий в прямоугольной декартовой системе координат вид
- оператора Лапласа, имеющий в прямоугольной декартовой системе координат вид
 ;
;
 - оператор векторного дифференцирования;
- оператор векторного дифференцирования;
 .
.
ОЗ – Обратная задача;
ОЗГ – обратная задача гравиметрииЖД
ФГМ – физико геологическая модель;
СГ – структурная гравиметрия;
ОЗСГ – обратные задачи структурной гравиметрии.
Введение
Интерпретация геофизических данных насквозь пронизана понятием модели. Это понятие столь часто и по разному поводу используется, что потеряло свое однозначное определение. Модель понимается как наше представление об окружающем мире и смысл вкладываемый в это понятие столь же разнообразен как и окружающий мир. В этом определении самое важное, видимо то, что всякое представление о каком либо предмете – это всего лишь субъективная модель этого предмета. Отсюда и вывод – познание невозможно вне введения моделей. Но для количественных определений такая широта вредна. Необходимо сообразно рассматриваемым задачам сузить это понятие, выявив его конструктивные и важные для построения математической теории интерпретации геофизических данных компоненты. Понятие модели может относиться к изучаемой среде, геофизическому полю, с помощью которого эта среда изучается и, наконец, связи между средой и полем. Извлечение информации из геофизических данных есть тоже модель. Но эта модель особого сорта. Она отражает используемый метод и характер извлекаемой информации. Конкретизация понятия модели относится к объекту описания. Описывается среда, дается описание поля и связи между моделями среды и поля, дается описание процессу извлечения информации. Далее, свойство модели – это конечно ее более простой чем реальность характер. Да и сама реальность доступная размышлению над ней это также всего лишь модель . В этой связи для каждой из объектных моделей могут быть введены многочисленные конкретизации отображающие желаемую для изучения объекта сторону. Модели вводятся для того, чтобы изучить конкретные свойства. Когда они изучены, следует без сожаления переходить к новой модели, отражающей иные свойство но неизбежно также неполной. Однако в методах интерпретации геофизических данных используемые модели – это не философские понятия. Они носят конкретный конструктивный характер и часто предопределяют самую возможность постановки интерпретационных задач и их математические свойства. Более того, сам процесс извлечения информации из геофизических данных – это процесс взаимной увязки моделей среды, поля, связей и потому основан на информационной модели геофизики и является потому моделью извлечения информации. Задачам реконструкции тех либо иных моделей среды по имеющимся моделям поля и связям между ними соответствуют конкретные интерпретационные уровни – модели извлечения информации из геолого – геофизических данных. В этой ситуации различным задачам геофизической интерпретации сопоставляются преобразования из конкретных уровней информационной модели геофизики.
Постановка интерпретационных задач состоит в определении моделей для изучаемой среды, модели для имеющегося поля и модели связи между этими объектами. Далее следует по двум последним моделям выделить элемент из первой. Это общая формулировка и она имеет многочисленные свои характерные черты в конкретных задачах. При этом различие в формах записи конкретных соотношений связи, типе используемых моделей оставляет неизменными эти элементы интерпретационной модели. Для каждого из метода, задача геофизической интерпретации имеет свой математический образ: задано поле 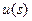 из класса возможных, определен класс моделей для характеристики свойств среды – это множество
из класса возможных, определен класс моделей для характеристики свойств среды – это множество 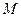 и конкретный элемент этого множества, конкретизирующий изучаемый объект обозначается
и конкретный элемент этого множества, конкретизирующий изучаемый объект обозначается 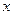 . Задано правило
. Задано правило 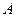 , связывающее элементы из
, связывающее элементы из 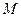 и
и 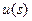 . Это правило записывается так:
. Это правило записывается так:  . Следует по известному
. Следует по известному 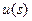 и «оператору»
и «оператору» 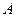 реконструировать
реконструировать  . Такова общая задача. Она возникает при обработке данных, она же возникает и при реконструкции содержательных физико – геологических моделей. Однако за этой общностью стоят существенные особенности при переходе к конкретным – содержательным вопросам. Один из этих вопросов состоит вот в чем. Модель для характеристики среды вводилась для того, чтобы с ее помощью описать, аппроксимировать изучаемый объект и это означает, что в
. Такова общая задача. Она возникает при обработке данных, она же возникает и при реконструкции содержательных физико – геологических моделей. Однако за этой общностью стоят существенные особенности при переходе к конкретным – содержательным вопросам. Один из этих вопросов состоит вот в чем. Модель для характеристики среды вводилась для того, чтобы с ее помощью описать, аппроксимировать изучаемый объект и это означает, что в 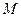 есть подходящий для этого элемент. Будет ли «похож» на него тот, который найден в результате реконструкции и что означает «похож»? Ответ далеко не очевиден.
есть подходящий для этого элемент. Будет ли «похож» на него тот, который найден в результате реконструкции и что означает «похож»? Ответ далеко не очевиден.
Без существенных изменений задача реконструкции элемента  по условию
по условию  возникает и в физике при обработке экспериментальных данных и имеет различные названия. Она называется обратной задачей, задачей редукции измерений. Эта задача относится к числу задач обработки данных, в отличие от интерпретационных задач, где проявляются более тонкие и сложно контролируемые эффекты. Ей посвящена обширная литература. Главная проблема, связанная с ее решением состоит в том, что из – за ошибок во входных данных и субъективизма в выборе моделей, ее решение может просто не существовать. Далее это решение может оказаться неединственным. И это последнее – характерная черта интерпретационных задач геофизики. Но даже если удастся обойти эти две трудности, может случиться так (и случается чаще всего), что небольшие погрешности в исходных данных влекут за собой несоизмеримо большие ошибки в результате реконструкции. Это явление называется неустойчивостью решения, а все в целом ( несуществование, неединственность, неустойчивость) и каждое по отдельности – некорректностью. Что касается существования, то эта трудность обходится проще всего. Достигается это просто заменой, в какой то мере формального требования
возникает и в физике при обработке экспериментальных данных и имеет различные названия. Она называется обратной задачей, задачей редукции измерений. Эта задача относится к числу задач обработки данных, в отличие от интерпретационных задач, где проявляются более тонкие и сложно контролируемые эффекты. Ей посвящена обширная литература. Главная проблема, связанная с ее решением состоит в том, что из – за ошибок во входных данных и субъективизма в выборе моделей, ее решение может просто не существовать. Далее это решение может оказаться неединственным. И это последнее – характерная черта интерпретационных задач геофизики. Но даже если удастся обойти эти две трудности, может случиться так (и случается чаще всего), что небольшие погрешности в исходных данных влекут за собой несоизмеримо большие ошибки в результате реконструкции. Это явление называется неустойчивостью решения, а все в целом ( несуществование, неединственность, неустойчивость) и каждое по отдельности – некорректностью. Что касается существования, то эта трудность обходится проще всего. Достигается это просто заменой, в какой то мере формального требования  , на более мягкое - осмысленное с физической точки зрения: разность между
, на более мягкое - осмысленное с физической точки зрения: разность между  и
и  для искомого элемента должна достигать наименьшего возможного значения. Этот результат уже нельзя назвать решением в строгом смысле. Он служит квазирешением – т.е. почти решением. Это лучшее что можно сделать и мы это делаем. Возникает теперь другой вопрос – вопрос о единственности и устойчивости обратной задачи. Поскольку связи между моделями среды и поля определены операторами
для искомого элемента должна достигать наименьшего возможного значения. Этот результат уже нельзя назвать решением в строгом смысле. Он служит квазирешением – т.е. почти решением. Это лучшее что можно сделать и мы это делаем. Возникает теперь другой вопрос – вопрос о единственности и устойчивости обратной задачи. Поскольку связи между моделями среды и поля определены операторами 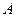 , а последние в качестве свого фундамента имеют уравнения математической физики, то исследование свойств корректности постановки обратных задач включает в себя исследование свойств устойчивой и однозначной разрешимости сооветствующих уравнений математической физии. Именно включают в себя а не исчерпываются этим. Оказывается что даже в таком идеализированном случае уравнений математической физики, идеально определенных данных, обратные задачи оказываются и неустойчивыми и чаще всего имеющими неединственное решение. Таково положение дел в физике при обработке экспериментальных данных, для которых и развиты в основном методы решения некорректных задач. Однако интерпретационные задачи геофизики имеют свою особую специфику. Здесь есть принципиальные отличия от задач физики да и от задач геофизики, связанных с обработкой данных. Этой особенностью служит с одной стороны неединственность их решения в достаточно общей постановке и сложноформализуемая дополнительная информация об искомом решении призванная компенсировать эффект неединственности с другой. При этом неединственность решения проистекает не только из неединственности решений соответствующих фундаментальных уравнений, что характерно и для уравнений математической физики. Таковы, например, обратные задачи теории потенциала. Она возникает также и из специфики соотношений между масштабами изучаемых объектов и допустимыми масштабами и характером систем наблюдений даже при условии, что соответствующие фундаментальные уравнения однозначно разрешимы, если разрешимы вообще. Мы не можем уйти от дискретного характера измерений в относительно небольшом числе точек на небольшой базе, определенной измерительной установкой. Соотношение: объект изучения - измерительный прибор оказывается принципиально отличным от того что формули руется в теоремах единственности где должны быть заданы непрерывные данных «от минус до плюс бесконечности». Мы не в состоянии точно учесть влияние целого ряда факторов, своих для каждого метода, но одинаково фатальных для свойств решаемой задачи. Таковы влияние рельефа, незнания физических параметров поверхностных участков. Все это влечет дополнительную неопределенность в решении задач реконструкции модели среды и делает еще более определяющим, выдвигает на передний план влияние на свойства решений особенностей используемых моделей и принципов, положенных в основу реконструкции. Одним из наиболее значимых отрицательных эффектов, возникающих в связи с неединственностью решений исходной задачи служит эффект скрытой эквивалентности. Это специфический для геофизики эффект и его надо обязательно учитывать при осмыслении результатов. О нем уже упоминалось и суть его состоит в том, что получаемое единственное и возможно даже устойчивое казирешение на
, а последние в качестве свого фундамента имеют уравнения математической физики, то исследование свойств корректности постановки обратных задач включает в себя исследование свойств устойчивой и однозначной разрешимости сооветствующих уравнений математической физии. Именно включают в себя а не исчерпываются этим. Оказывается что даже в таком идеализированном случае уравнений математической физики, идеально определенных данных, обратные задачи оказываются и неустойчивыми и чаще всего имеющими неединственное решение. Таково положение дел в физике при обработке экспериментальных данных, для которых и развиты в основном методы решения некорректных задач. Однако интерпретационные задачи геофизики имеют свою особую специфику. Здесь есть принципиальные отличия от задач физики да и от задач геофизики, связанных с обработкой данных. Этой особенностью служит с одной стороны неединственность их решения в достаточно общей постановке и сложноформализуемая дополнительная информация об искомом решении призванная компенсировать эффект неединственности с другой. При этом неединственность решения проистекает не только из неединственности решений соответствующих фундаментальных уравнений, что характерно и для уравнений математической физики. Таковы, например, обратные задачи теории потенциала. Она возникает также и из специфики соотношений между масштабами изучаемых объектов и допустимыми масштабами и характером систем наблюдений даже при условии, что соответствующие фундаментальные уравнения однозначно разрешимы, если разрешимы вообще. Мы не можем уйти от дискретного характера измерений в относительно небольшом числе точек на небольшой базе, определенной измерительной установкой. Соотношение: объект изучения - измерительный прибор оказывается принципиально отличным от того что формули руется в теоремах единственности где должны быть заданы непрерывные данных «от минус до плюс бесконечности». Мы не в состоянии точно учесть влияние целого ряда факторов, своих для каждого метода, но одинаково фатальных для свойств решаемой задачи. Таковы влияние рельефа, незнания физических параметров поверхностных участков. Все это влечет дополнительную неопределенность в решении задач реконструкции модели среды и делает еще более определяющим, выдвигает на передний план влияние на свойства решений особенностей используемых моделей и принципов, положенных в основу реконструкции. Одним из наиболее значимых отрицательных эффектов, возникающих в связи с неединственностью решений исходной задачи служит эффект скрытой эквивалентности. Это специфический для геофизики эффект и его надо обязательно учитывать при осмыслении результатов. О нем уже упоминалось и суть его состоит в том, что получаемое единственное и возможно даже устойчивое казирешение на 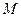 может оказаться приближением не к тому под что строился класс
может оказаться приближением не к тому под что строился класс 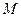 , а к чему то эквивалентному по полю но бессмысленному по своим содержательным, прежде всего физико – геологическим свойствам. Это может произойти и происходит за счет того что
, а к чему то эквивалентному по полю но бессмысленному по своим содержательным, прежде всего физико – геологическим свойствам. Это может произойти и происходит за счет того что  позволяет этот эффективный, эквивалентный элемент аппроксимировать ( т.е. приблизить) еще лучше чем тот на который мы рассчитывали. Это может быть совершенно неожиданным и побочным эффектом. Но самое печальное состоит в том, что в значительном числе случаев этот эффект не контролируем.
позволяет этот эффективный, эквивалентный элемент аппроксимировать ( т.е. приблизить) еще лучше чем тот на который мы рассчитывали. Это может быть совершенно неожиданным и побочным эффектом. Но самое печальное состоит в том, что в значительном числе случаев этот эффект не контролируем.
Решение интерпретационных геофизических задач происходит в условиях «проклятия эквивалентности» - эквивалентности явной или скрытой. В этой ситуации не менее важным, чем формирование модельных представлений является использование принципов извлечения информации. Принцип квазирешений на множестве обладающем свойством единственности решения имеет в качестве ограничения возможные эффекты скрытой эквивалентности. Недостаточность принципа квазирешений для интерпретационных геофизических задач вынуждает к введению иных подходов. Важнейшие из них состоят в дополнительном введении критериев, характеризующих свойства допустимых моделей с точки зрения их соответствия имеющимся комплексам геолого – геофизических сведений об изучаемом объекте. Эта последняя информация может быть двух видов.
Во – первых, это система предпочтений (термин В.Н. Страхова) отражающая информацию относительно состояния изучаемого объекта. Эта система предпочтений имеет вид критерия оптимальности – вычисляемого значения качества той либо иной модели Например, в качестве такого критерия может выступать критерий максимума меры подобия между изучаемым объектом и некоторыми эталонами. Другим критерием может служить требование минимальности корректив, которые следует внести в некоторую заданную, известную модель среды. Этот критерий легко обобщается на случай, когда коррективы допустимо вводить только в выделенных частях модели, а на допустимых коррективах определена система «предпочтений». Эти методы имеют одно общее начало – критериальный принцип доопределения в постановке обратных задач. Конечно каждый вид критерия оптимальности порождает свои свойства в решении также, как отсутствие критерия порождает эффект скрытой эквивалентности. Однако эти свойства определены и процесс управляем. Вопросы этого направления разбираются в гл. 5.
Иной вид информации о модели, выражающий ее приемлемость или не приемлемость это эволюционно – динамическая информация. Она представляет собой совокупность предположений и гипотез о схеме формирования изучаемого объекта. Отражает его генезис и выражается в виде принятия эволюционных законов, которым подчинена модель – современное состояние есть конечное значение в этой эволюционной цепочке. Оно должно быть введено из нее при соответствующем подборе геодинамических параметров, управляющих процессом эволюции. Эти последние параметры могут быть связаны с моделями наблюдаемых физических полей, и вся система оказывается вполне определенной. По сути это та же упоминавшаяся выше система предпочтений, но порожденная соответствием реконструируемой модели явно сформулированным эволюционным законам формирования и развития изучаемого геологического объекта. Конечно, говоря об формулируемых эволюционных законах следует учитывать два обстоятельства. Во первых, сами за
|
из
5.00
|
Обсуждение в статье: Список использованных обозначений |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

