 |
Главная |
Интерпретационная модель геофизических исследований
|
из
5.00
|
Процесс интерпретации исходных геофизических данных – наблюдаемых, это процесс движения от низшего информационного уровня к высшему с использованием связей между разноуровенными моделямиобъектов, составляющих информационную модель. Этот процесс складывается из системы последовательных переходов от наблюдаемых физическим полям, от них далее к физическим моделям, и в конечном итоге к геологической модели. Каждый из этих переходов сопровождается процедурами решением задач реконструкции параметров верхнего информационного уровня по параметрам нижнего и заданным связям (рис.4).

На одном конце информационной модели геофизики находятся геологические параметры T,подлежащие определению, а на другом наблюдаемые  ,которые измерены, кроме того, с ошибкой
,которые измерены, кроме того, с ошибкой  , так что реально задано:
, так что реально задано: 
 это символическая запись погрешностей, осложняющих некоторые точно заданные данные, и наличие которых неизбежно ведет к погрешностям в реконструкции как физической, так и геологической модели. Они выделяются из состава величин, входящих в наблюдаемые для того, чтобы подчеркнуть дальнейшее поэтапное влияние погрешностей, возникающих при продвижении в процессе реконструкции геологической модели.
это символическая запись погрешностей, осложняющих некоторые точно заданные данные, и наличие которых неизбежно ведет к погрешностям в реконструкции как физической, так и геологической модели. Они выделяются из состава величин, входящих в наблюдаемые для того, чтобы подчеркнуть дальнейшее поэтапное влияние погрешностей, возникающих при продвижении в процессе реконструкции геологической модели.
Интерпретациярезультатов геофизических наблюдений состоит в переходе от наблюдаемых  к геологическим параметрам
к геологическим параметрам  . Этот переход осуществляется поэтапно с помощью процедур, являющихся элементами интерпретационной модели. Они имеют содержательный смысл:
. Этот переход осуществляется поэтапно с помощью процедур, являющихся элементами интерпретационной модели. Они имеют содержательный смысл:
· обработка (реконструкция физических полей);
· реконструкция физических моделей;
· реконструкция геологических моделей.
Элементарные процедуры группируются в схемы геофизической и геологической интерпретации. Процедурно они реализуются операциями обратными к установленным связям и составляют содержание постановок обратных задач. Набор элементов и процедур, обеспечивающий переход от нижних этажей информационной модели к верхним и сопутствующие ему оценки возникающих погрешностей, составляет содержание интерпретационной модели геофизики.
В соответствии с построенной информационной моделью этот переход предполагает:
1. Переход от наблюдаемых  к физическим полям
к физическим полям  Этотэтап называется обработкой геофизических данныхи реализуется оператором обработки
Этотэтап называется обработкой геофизических данныхи реализуется оператором обработки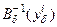 :
:

| (1.1) |
Этот оператор применяется к исходным данным и включает в себя две компоненты. Первая  – это некоторая операция строго обратная к точному (но возможно неизвестному точно) эталонирующему преобразованию.
– это некоторая операция строго обратная к точному (но возможно неизвестному точно) эталонирующему преобразованию.  – единичное преобразование:
– единичное преобразование:  .Вторая компонента
.Вторая компонента 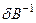 ответственна за погрешности, связанные с отличием реально используемых процедур расчета от требуемых. Целью операции обработки является исключение разного рода погрешностей: аппаратурных, калибровочных, а также приведение наблюдаемых к виду и форме, пригодных для последующего использования при восстановлении физических параметров – модели физического поля. В частности оператор обработки может конструироваться из принципов компенсации мультипликативных (искажающих) и аддитивных помех. Характер обработки зависит и от того, какие модельные представления о характере физического поля, физических параметрах и их взаимосвязи на последующих этапах предстоит использовать. Процедурно, операция обработки - это решение обратной задачи для эталонирующего преобразования. Содержательно - это приближенная реконструкция модели физического поля, подлежащего последующему анализу.
ответственна за погрешности, связанные с отличием реально используемых процедур расчета от требуемых. Целью операции обработки является исключение разного рода погрешностей: аппаратурных, калибровочных, а также приведение наблюдаемых к виду и форме, пригодных для последующего использования при восстановлении физических параметров – модели физического поля. В частности оператор обработки может конструироваться из принципов компенсации мультипликативных (искажающих) и аддитивных помех. Характер обработки зависит и от того, какие модельные представления о характере физического поля, физических параметрах и их взаимосвязи на последующих этапах предстоит использовать. Процедурно, операция обработки - это решение обратной задачи для эталонирующего преобразования. Содержательно - это приближенная реконструкция модели физического поля, подлежащего последующему анализу.
Запись (1) является символической и предназначена для пояснения характера возникающих в процессе реконструкции моделей погрешностей. В линейном приближении к процедурам обработки можно записать:

Откуда:
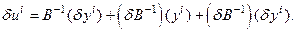
| (1.2) |
Таким образом, погрешность, возникающая в результате применения процедур обработки в подлежащих интерпретации физических полях, складывается как из исходных погрешностей в наблюдаемых  ,так и погрешности процедур обработки, которые переводят в разряд погрешности точные компоненты наблюдаемых
,так и погрешности процедур обработки, которые переводят в разряд погрешности точные компоненты наблюдаемых  и увеличивают исходные погрешности наблюдаемых
и увеличивают исходные погрешности наблюдаемых 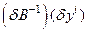 .
.
2. Переход от найденных приближений к модели физических полей  к физическим параметрам
к физическим параметрам  , которые также будут неизбежно осложнены погрешностями:
, которые также будут неизбежно осложнены погрешностями:  . Этот переход называется решением обратных задачгеофизики и реализуется с помощью операторов
. Этот переход называется решением обратных задачгеофизики и реализуется с помощью операторов  приближенногокточномуобратному
приближенногокточномуобратному 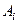 . Оператор
. Оператор  также складывается из компонент – некоторого, неизвестного точного обратного
также складывается из компонент – некоторого, неизвестного точного обратного  и погрешности
и погрешности  ответственной за неточное знание и неумение правильно вычислять оператор, обратный к уравнениям математической физики:
ответственной за неточное знание и неумение правильно вычислять оператор, обратный к уравнениям математической физики:

| (1.3) |
Использование записи  – достаточно условно, поскольку в строгом смысле обратного к
– достаточно условно, поскольку в строгом смысле обратного к 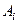 может просто не существовать, либо он может быть неограниченным - невычисляемым оператором. Эту запись можно понимать в том смысле, что для некоторых характерных для данной геолого-геофизической ситуации точных данных - физических полей
может просто не существовать, либо он может быть неограниченным - невычисляемым оператором. Эту запись можно понимать в том смысле, что для некоторых характерных для данной геолого-геофизической ситуации точных данных - физических полей  и физических параметров
и физических параметров  , таких что
, таких что .Тогда
.Тогда  представляет собой совокупную погрешность, связанную с использованием приближенного оператора решения обратной задачи. Это многокомпонентная величина, включающая в себя погрешности, связанные с заменой точных формул решения прямой задачи их приближенными аналогами, использованием специальных алгоритмов для обеспечения устойчивости решения, степени соответствия используемой модели физических параметров их реальному распределению. В реальных ситуациях величина
представляет собой совокупную погрешность, связанную с использованием приближенного оператора решения обратной задачи. Это многокомпонентная величина, включающая в себя погрешности, связанные с заменой точных формул решения прямой задачи их приближенными аналогами, использованием специальных алгоритмов для обеспечения устойчивости решения, степени соответствия используемой модели физических параметров их реальному распределению. В реальных ситуациях величина  может быть весьма значительной и самым фатальным образом влиять на результат решения обратной задачи.
может быть весьма значительной и самым фатальным образом влиять на результат решения обратной задачи.
Также как это было сделано выше для процедур обработки в линейном приближении к операторам прямых задач, можно записать:


| (1.4) |
Последовательное применение процедур обработки и решения обратных задач называется геофизической интерпретацией данных. Целью геофизической интерпретации служит восстановление физических параметров геологических объектов. Как видно из формулы (4) погрешности реконструкции физических параметров резко возрастают.
3. Переход от физических параметров  к геологическим
к геологическим  .Этот этап называется обращением физико-геологических зависимостейи состоит в расчете с использованием приближенной зависимости
.Этот этап называется обращением физико-геологических зависимостейи состоит в расчете с использованием приближенной зависимости  . Для простоты изложения предполагается, что уравнение
. Для простоты изложения предполагается, что уравнение  , определяющее петрофизические связи может быть разрешено относительно параметров
, определяющее петрофизические связи может быть разрешено относительно параметров  и представлено в форме
и представлено в форме 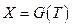 . Это конечно очень сильное допущение, но для текущих демонстрационных целей оно вполне допустимо. Следуя уже дважды описанной схеме, легко получаем:
. Это конечно очень сильное допущение, но для текущих демонстрационных целей оно вполне допустимо. Следуя уже дважды описанной схеме, легко получаем:  , где
, где

Подставляя в последнее выражение вместо 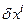 выражение (4), далее заменяя
выражение (4), далее заменяя  на его значение в соответствии с (2), получим состав компонент, влияющих на погрешность в построении геологической модели. Исходная погрешность в наблюдаемых разрастается «как снежный ком».
на его значение в соответствии с (2), получим состав компонент, влияющих на погрешность в построении геологической модели. Исходная погрешность в наблюдаемых разрастается «как снежный ком».
Переход от наблюдаемых к геологическим параметрам называется геологической интерпретацией геофизических данных. Она включает в себя последовательность:
· обработку геофизических данных;
· решение обратных задач геофизики;
· обращение физико-геологических зависимостей.
В интерпретационной геофизической модели ее элементы не являются полностью независимыми. Они образуют единое взаимосвязанное целое. Способ, характер и погрешность измерения наблюдаемых в значительной степени определяет последующие используемые процедуры обработки. Найденные физические поля, а точнее интерпретируемые его компоненты, полученные в результате обработки, определяют последующие постановки обратных задач геофизики. Характер определяемых физических параметров предопределяет и допустимые процедуры нахождения геологических параметров. Таким образом, окончательная погрешность реконструкции геологической модели складывается из комбинации погрешностей на всех этапах реконструкции параметров.
Погрешность измерений  представляет собой первичную погрешность в результатах измерений как аппаратурного, так и методического происхождения. Ее снижение осуществляется, во-первых, совершенствованием аппаратурной базы, повышением ее точности, чувствительности, во-вторых, наращиванием кратности наблюдений, в-третьих, совершенствованием методических приемов производства полевых работ. Сюда, например, относится повышение детальности геофизической съемки, переход от профильных к площадным наблюдениям (переход от двухмерной к трехмерной сейсморазведке). Эти погрешности передаются обрабатывающим процедурам и могут быть в значительной степени погашены ими. Так происходит, например, при подавлении нерегулярных компонент волнового поля интерференционными системами. Однако снижение этой погрешности само по себе, даже при полном сведении ее к нулю, не избавляет от погрешностей в последующих этапах. Оно может быть эффективным лишь тогда, когда сопровождается повышением точности всех последующих этапов геологической интерпретации.
представляет собой первичную погрешность в результатах измерений как аппаратурного, так и методического происхождения. Ее снижение осуществляется, во-первых, совершенствованием аппаратурной базы, повышением ее точности, чувствительности, во-вторых, наращиванием кратности наблюдений, в-третьих, совершенствованием методических приемов производства полевых работ. Сюда, например, относится повышение детальности геофизической съемки, переход от профильных к площадным наблюдениям (переход от двухмерной к трехмерной сейсморазведке). Эти погрешности передаются обрабатывающим процедурам и могут быть в значительной степени погашены ими. Так происходит, например, при подавлении нерегулярных компонент волнового поля интерференционными системами. Однако снижение этой погрешности само по себе, даже при полном сведении ее к нулю, не избавляет от погрешностей в последующих этапах. Оно может быть эффективным лишь тогда, когда сопровождается повышением точности всех последующих этапов геологической интерпретации.
Погрешность обрабатывающих процедур  не только трансформирует погрешности в наблюдаемых, но и переводит в разряд погрешностей сами наблюдаемые. Большое число примеров погрешностей в обрабатывающих процедурах дает сейсморазведка. Ошибки в коррекции статики, выборе параметров фильтрации, величин скоростей миграционных преобразований может привести к полной перестройке волновой картины относительно истинной. Значительные погрешности в обрабатывающих процедурах содержаться и при обработке данных геофизических исследований скважин. Сюда относятся недоучет влияния скважины, промытой зоны и многое другое. Минимизация погрешностей обрабатывающих процедур, чаще всего, осуществляется на этапе опытно - методических работ. Это одна из их основных задач. Главной целью использования обрабатывающих процедур служит формирование из наблюдаемых параметров физического поля, соответствующих последующей модели, положенной в основу методов решения обратных задач и обращения физико-геологических зависимостей. В этой связи снижение погрешностей обрабатывающих процедур будет иметь смысл лишь в том случае, когда оно согласовано с точностью последующих процедур получения из обработанного поля физических и геологических параметров изучаемого объекта.
не только трансформирует погрешности в наблюдаемых, но и переводит в разряд погрешностей сами наблюдаемые. Большое число примеров погрешностей в обрабатывающих процедурах дает сейсморазведка. Ошибки в коррекции статики, выборе параметров фильтрации, величин скоростей миграционных преобразований может привести к полной перестройке волновой картины относительно истинной. Значительные погрешности в обрабатывающих процедурах содержаться и при обработке данных геофизических исследований скважин. Сюда относятся недоучет влияния скважины, промытой зоны и многое другое. Минимизация погрешностей обрабатывающих процедур, чаще всего, осуществляется на этапе опытно - методических работ. Это одна из их основных задач. Главной целью использования обрабатывающих процедур служит формирование из наблюдаемых параметров физического поля, соответствующих последующей модели, положенной в основу методов решения обратных задач и обращения физико-геологических зависимостей. В этой связи снижение погрешностей обрабатывающих процедур будет иметь смысл лишь в том случае, когда оно согласовано с точностью последующих процедур получения из обработанного поля физических и геологических параметров изучаемого объекта.
Погрешность оператора решения обратной задачи 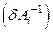 является наиболее значимой. Она проявляется не только из погрешностей вычислений, но в главном состоит в эффектах, могущих привести к бессодержательности с геологической точки зрения сами получаемые решения даже при отсутствии собственно вычислительных погрешностей. Это погрешности иного рода – погрешности, связанные с эффектами эквивалентности, в том числе и скрытой эквивалентности. Они связаны с ошибками в модельных представлениях, положенных в основу процедур решения обратных задач. Описание и анализ такого рода эффектов приводится в разделах 1.4.3 и 3.3.
является наиболее значимой. Она проявляется не только из погрешностей вычислений, но в главном состоит в эффектах, могущих привести к бессодержательности с геологической точки зрения сами получаемые решения даже при отсутствии собственно вычислительных погрешностей. Это погрешности иного рода – погрешности, связанные с эффектами эквивалентности, в том числе и скрытой эквивалентности. Они связаны с ошибками в модельных представлениях, положенных в основу процедур решения обратных задач. Описание и анализ такого рода эффектов приводится в разделах 1.4.3 и 3.3.
Погрешность, допускаемая при формировании и использовании физико-геологических зависимостей, определяется, во-первых, соответствием геолого-геофизической ситуации, при которой эти зависимости были получены той, для которой они используются, а во-вторых, собственно погрешностью прогноза. Общей закономерностью является увеличение точности прогноза при использовании большего числа определенных физических параметров. С увеличением числа используемых и известных физических параметров снижается влияние на точность прогноза неучтенных геолого-геофизических факторов.
Приведенная интерпретационная модель основана на объективных взаимосвязях между различными компонентами геофизических данных, нашедших отражение в информационной модели геофизики. Неучет ее, попытка “забежать вперед”, “перескочить” отдельные элементы при построении процедур интерпретации геофизических данных, например, при попытке геологической интерпретации непосредственно компонент, полученных после обработки наблюдаемых, без перехода к физическим параметрам, неизбежно приведут к искажению и потере объективной информации заложенной в геофизических данных.
Модели и их свойства
В зависимости от описываемых классов объектов выделяют три типа моделей – модели, относящиеся к описанию среды, модели, относящиеся к описанию поля и модели связей между моделями среды и поля. К первому типу относятся геологические и физические модели. Ко второму – модели физического поля и наблюдаемой, к третьему – геолого-геофизические связи, уравнения математической физики и эталонирующие преобразования.

Рис.1.5 Типы моделей.
1.3.1 Модели среды по своему назначению подразделяются на аппроксимационные и динамические.
Аппроксимационные модели, как это следует из названия, предназначены для аппроксимации среды набором элементарных объектов из заданного класса. Этот класс обозначаем M. Чаще всего, в качестве аппроксимирующих элементов выступают элементарные геометрические объекты. Например, это система призм, уступов, многоугольников, предназначенных для аппроксимации плотностной модели геологического объекта. Каждый элемент аппроксимирующей системы имеет свои параметры – размеры, глубину залегания, плотность, если речь идет о плотностной модели. Перечень этих параметров составляет параметризацию модели, а ограничения, накладываемые на их значения в связи с дополнительной информацией, в том числе и в связи с другими моделями, требованиями согласованности с геофизическими полями, образуют систему связей. Важной характеристикой аппроксимационной модели служит погрешность аппроксимации множеством M элемента  . Элемент
. Элемент  принадлежит некоторой более общей модели
принадлежит некоторой более общей модели 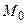 , например, распределению плотности как функции координат. Если заранее известно, что изучаемый объект принадлежит некоторому множеству
, например, распределению плотности как функции координат. Если заранее известно, что изучаемый объект принадлежит некоторому множеству  , то
, то  характеризует аппроксимационную способность M для описания
характеризует аппроксимационную способность M для описания  .
.
Динамические моделипредназначены для характеристики процессов, происходящих в изучаемой среде. Типичным примером такого рода моделей служат тектонофизические модели, системы палеореконструкций, следующих из рассмотрений обратных задач геодинамики, модели переноса вещества в термогравитационных и термохимических мантийных конвекций. Динамические модели определяются заданием уравнений, которым подчиняется процесс и системой параметров, его характеризующих – например, распределениями напряжений, физико-механическими свойствами среды. Типичным примером динамической модели служит уравнение Навье – Стокса, характеризующего вязкое течение жидкости (например, Ньютоновой и несжимаемой) и его частные случаи – приближение Буссинеска и др. Параметрами служат система внешних сил, коэффициенты вязкости, плотность. Наряду с однофазными движениями, могут быть рассмотрены многофазные, подчиняющиеся более сложным уравнениям, следующих из законов фазовых превращений. Динамические модели имеют своей целью с той либо иной степенью точности описать эволюцию рассматриваемой геосистемы, прежде всего с позиций механики сплошных сред. Однако чаще всего удается с большей либо меньшей долей подобия описать лишь фрагменты этой эволюции и оправдать выдвижение гипотез о развитии и формировании современного вида системы.
Модели среды по характеру используемых параметров подразделяются на содержательные и эффективные.
Содержательные моделинаиболее ясные и пригодные для физико-геологических выводов. Они имеют своей целью описание объекта в традиционных физических или геологических терминах. Сюда относятся: конкретные физические параметры, такие как плотность, упругие параметры, электрические, магнитные свойства и многое другое; физико-геологические параметры, такие как литологические возрастные (стратиграфические), емкостные, коллекторские; геометрические параметры используемых моделей, характеризующие взаиморасположение компонент модели. Вопрос о перечне параметров в содержательных моделях чаще всего тривиален, поскольку он предопределен видом выбранной физико-геологической модели. Однако, весьма существенен вопрос о связях между параметрами и их проявлениями в физических полях.
Эффективные моделивводятся и используются, чаще всего, для построения и изучения содержательных физико-геологических моделей. Среди эффективных моделей выделяются модели эффективного параметра, формально эквивалентные и комплексные модели.
Модели эффективного параметрапредставляют собой результат применения эвристических, чаще всего, нелинейных преобразований к наблюдаемым или физическим полям. Результат такого преобразования дает распределение некоторой величины, для которой экспериментально установлены случаи связи между особенностями ее пространственного распределения и некоторыми элементами физико-геологической модели среды. Яркими представителями этих приемов служат метод полного нормированного градиента В. М. Березкина, метод яркого пятна при решении задач выделения аномальных зон в геологической модели. Эффективный параметр не имеет размерность конкретного физического параметра, а даже если и имеет, то рассчитанное от него с помощью уравнений математической физики поле не соответствует исходному. Это принципиально важное свойство эффективных моделей. Этот параметр подобен изображению объекта в инфракрасном диапазоне излучения – несет о нем полезную информацию, но отличается от того, что видно в обычном – видимом диапазоне спектра. Эту аналогию можно продолжить, считая модели эффективного параметра некоторыми специального вида изображениями реальной среды, возможно и в некотором «экзотическом» свете.
Формально эквивалентные моделипредставляют собой особый класс моделей среды. Как уже указывалось при обсуждении интерпретационной модели, характерной чертой обратных задач геофизики является неоднозначность их решения. Это фундаментальное свойство, называемое эквивалентностью, состоит в том, что одному и тому же полю соответствует бесконечно много распределений физического параметра, различающихся существенно между собой, но эквивалентных по полю. Это формально эквивалентные модели. Их бесконечно много, даже в том случае, если конкретная вычислительная технология построения распределения физического параметра приводит лишь к одному решению. Это может достигаться особенностями алгоритма либо выбором аппроксимирующей модели. Технология, приводящая к построению единственного решения, не сопровождающаяся тщательным геолого-геофизическим осмыслением и увязкой принципов, приводящих к выделению единственного решения, приводит к формально эквивалентной модели. Получаемая в результате решения обратной задачи формально эквивалентная модель, ни в коем случае не должна рассматриваться как итоговая, но должна быть рассмотрена как трансформация поля в распределение параметра с размерностью физического свойства, результат расчета поля от которого приводит к исходному полю. Формально – эквивалентная модель, в отличие от модели эффективного параметра, даже визуально может не напоминать «истинную» и отличаться от нее принципиально во всех отношениях, кроме эквивалентности по полю.
Комплексные моделипредставляют собой симбиоз различных моделей, приведенных к единому параметру (правильно говорить об интегрированной модели) либо систему содержательных и эффективных моделей.
1.3.2. Модели поляв содержательном отношении определены связями, положенными в основу интерпретационной модели между средой и полем. Что же касается формы, то модель поля может быть дискретной, что включает в себя описание поля в виде дискретных массивов значений, либо аппроксимационной.
Дискретная модельэто простейшая модель, требующая уточнения лишь в том, что означают дискретные отсчеты и куда они отнесены. Параметрами этой модели служат область задания значений, координаты точек.
Аппроксимационная модель поляэто способ его описания с помощью некоторого набора элементарных объектов – например элементарных полей. Исходное поле, заданное массивом своих значений заменяется набором элементарных объектов, с небольшим числом параметров – меньшим, чем число элементов массива, но так, что эта совокупность аппроксимирует исходные значения с точностью не хуже заданной. Этим приемом достигается решение трех задач: сжатие информации – описание большого числа элементов с помощью небольшого числа параметров; анализ структуры поля по распределению значений параметров аппроксимирующих элементарных полей (это может быть полезным для формирования модели среды); фильтрация и борьба с помехами.
Приведенные способы описания поля могут быть применены для описания собственно модели физического поля или наблюдаемой, некоторой трансформанты – преобразования поля, которое используется в уравнениях связи и в последующих процедурах реконструкции моделей среды либо атрибутов.
Атрибуты поля– понятие, более всего используемое в сейсморазведке [1]. К атрибутам поля относятся специального типа наблюдаемые, пересчитываемые в параметры модели среды по заданным экспериментально зависимостям. Это собирательное понятие. Для сложных многокомпонентных наблюдаемых атрибуты – это выделенные характеристики поля или его трансформант, которые составляют лишь часть наблюдаемых, используемых далее в специализированной для этих атрибутов технологии анализа. Цель этого анализа – оценка некоторых параметров введенной эффективной модели среды. Именно для характеристики этой части используется понятие атрибут с последующим его наименованием – например, атрибуты преобразования Гильберта
1.3.3. Модель связейпредставляет собой стержень конструируемого интерпретационного процесса. Эти связи предопределяют суть процедур обработки, решения обратных задач и реконструкции модели среды – содержательной либо эффективной. Связи могут быть детерминированными, статистическими и эвристическими.
Детерминированные связиимеют вид интегральных, дифференциальных уравнений. Это связи между физическими моделями среды и моделями физического поля - уравнения математической физики. Они составляют вычислительную основу при реконструкции физических моделей и построении формально эквивалентных моделей.
Статистические связиоснованы на выявленных корреляционно-регрессионных зависимостях между параметрами среды и, чаще всего, атрибутами поля. Статистические связи используются для построения моделей эффективного параметра, а при дополнительных условиях проверки и корректировки результата моделированием могут использоваться и для получения содержательных моделей.
Эвристические связидают широкий простор для конструирования эффективных моделей среды. Типичным и, по видимому, непревзойденным по эффективности примером эвристических связей дает метод полного нормированного градиента В.М. Березкина. Он основан на том, что эффективный параметр, называемый полным нормированным градиентом гравитационного поля , отображает характеристики среды. Эта эвристическая связь основана на экспериментально установленном факте, состоящем в том, что экстремумы полного нормированного градиента пространственно приурочены к аномальным зонам в изучаемой физико-геологической модели среды.
Другими примерами эвристических преобразований могут служить многочисленные процедуры параметрической фильтрации поля, основанные на таком же постулируемом предположении.
|
из
5.00
|
Обсуждение в статье: Интерпретационная модель геофизических исследований |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

