 |
Главная |
Итерационная регуляризация
|
из
5.00
|
Решение уравнения
 (4.39)
(4.39)
может быть осуществлено методом итерацийи этот достаточно простой прием, в определенных ситуациях служит регуляризующим алгоритмом. Простейшая итерационная схема:
 (4.40)
(4.40)
сходится к точному решению задачи (39) [3, стр.92] при любом выборе  , если : А- самосопряженный, положительно определенный оператор в гильбертовом пространстве Х;
, если : А- самосопряженный, положительно определенный оператор в гильбертовом пространстве Х;  - существует и, кроме того,
- существует и, кроме того,  , где
, где  - наибольшее собственное число оператора А. Если у задано с погрешностью
- наибольшее собственное число оператора А. Если у задано с погрешностью 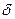 (задано
(задано  ), и процессе остановлен на шаге N, то обозначим полученный при итерации элемент
), и процессе остановлен на шаге N, то обозначим полученный при итерации элемент 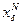 . Если предположить, что при точных данных
. Если предположить, что при точных данных 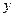 - аналогичное –
- аналогичное –  приближение есть
приближение есть  то, в силу неравенства треугольника
то, в силу неравенства треугольника 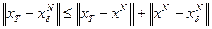 , где
, где  - гипотетическое точное решение (39) при точных данных.
- гипотетическое точное решение (39) при точных данных.
При 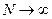 , в силу сходимости итерационного процесса
, в силу сходимости итерационного процесса  и, следовательно, алгоритм (40) будет регуляризирующим тогда, когда
и, следовательно, алгоритм (40) будет регуляризирующим тогда, когда  .
.
Перепишем схему (40) для точных и приближенных данных:

Кроме того, будем считать для простоты 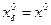 . Тогда получим:
. Тогда получим:
 (3.41)
(3.41)
Если выбрать N-число итераций так, чтобы N=N(δ),
 ,
,
то  , и алгоритм (40) является регуляризирующим. Последовательность
, и алгоритм (40) является регуляризирующим. Последовательность 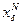 является регуляризованной последовательностью приближений.
является регуляризованной последовательностью приближений.
Нетрудно заметить, что величина 
как функция номера итерации n является возрастающей. Отсюда, в частности, следует вывод, что при заданном уровне погрешности δ в правой части (39) увеличивать число итераций выше уровня  , обеспечивающего достижение заданной невязки неоправданно. Начиная с номера
, обеспечивающего достижение заданной невязки неоправданно. Начиная с номера  , это приведет не к улучшению, а к ухудшению свойств решения, т.е. его удалению решения с приближенными данными от точного. Поэтому число итераций в процессе (40) должно быть регламентировано реально имеющейся оценкой погрешности в правой части уравнения (39). Возрастание функции С(n) приводит и к рекомендации по выбору этого числа требуемых итераций. Итерационный процесс (40) должен быть прерван, когда достигнута заданная невязка. В частности, при точно заданном операторе А выполнено неравенство:
, это приведет не к улучшению, а к ухудшению свойств решения, т.е. его удалению решения с приближенными данными от точного. Поэтому число итераций в процессе (40) должно быть регламентировано реально имеющейся оценкой погрешности в правой части уравнения (39). Возрастание функции С(n) приводит и к рекомендации по выбору этого числа требуемых итераций. Итерационный процесс (40) должен быть прерван, когда достигнута заданная невязка. В частности, при точно заданном операторе А выполнено неравенство:
 .
.
В этом состоит реализация выбора числа итераций по принципу невязки. Роль параметра регуляризации играет величина обратная к номеру итерационного процесса. В том случае, когда оператор 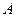 задан с погрешностью h, следует воспользоваться уже описанным выше принципом обобщенной невязки.
задан с погрешностью h, следует воспользоваться уже описанным выше принципом обобщенной невязки.
Применимость простейшей итерационной схемы (40) ограничена требованием самосопряженности и положительной определенность оператора 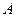 . В том случае, когда этот оператор не является самосопряженным и положительным, умножая на сопряженный к нему правую и левую части уравнения (39), приходим к итерационной процедуре:
. В том случае, когда этот оператор не является самосопряженным и положительным, умножая на сопряженный к нему правую и левую части уравнения (39), приходим к итерационной процедуре:

Все рассуждения о сходимости для (40) дословно повторяют приведенные выше с заменой оператора А на А*А. При этом оценка (41) примет вид:
 .
.
Выводы.
Приведенные конспективно результаты по методам решения некорректных задач не охватывают даже малой части того, что сделано полезного сегодня в этом направлении. Однако изложенного все же вполне достаточно, чтобы усвоить идеологию подхода, построить принципиальную схему регуляризации для широкого круга задач, а самое главное, понять, как работают те либо иные реализованные процедуры. Для дальнейшего, углубленного ознакомления с предметом рекомендую, например, книги [1-4]. В геофизических приложениях и, в частности гравимагнитометрии, развитию методов решения неустойчивых задач посвящено исключительно много работ В.Н. Страхова. Приведем одну из них, наиболюю позднюю на момент написания этих строк [5]. П приведенной в ней библиографии легко отследить остальные работы. Особенностью рассмотрений служит предположение о том, что помеха и полезный сигнал ортогональны. Его введение позволяет построить эффективные алгоритмы решения некорректных задач, однако само оно, как всякое предположение имеет свой круг применимости.
Следующее обстоятельство является общим при рассмотрении неустойчивых задач описанными методами. Предполагается, что задача
 (4.42)
(4.42)
при некоторых точных данных имеет одно и только решение 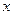 . Способы конструирования регуляризирующих алгоритмов состоят в приближенном расчете по приближенным данным (Аh, yδ) некоторого элемента
. Способы конструирования регуляризирующих алгоритмов состоят в приближенном расчете по приближенным данным (Аh, yδ) некоторого элемента 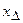 , такого, что при
, такого, что при 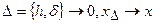 . Еще раз подчеркнем, что
. Еще раз подчеркнем, что 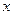 – это решение (42), соответствующее точным данным
– это решение (42), соответствующее точным данным 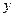 (отвлечемся от погрешностей в операторе
(отвлечемся от погрешностей в операторе 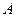 и предположим, что все они сконцентрированы в
и предположим, что все они сконцентрированы в  ). Существование этого точного элемента предполагает, что
). Существование этого точного элемента предполагает, что  , и последнее обстоятельство является принципиальным. С самого начала М – это конструкция для приближенного описания объекта и, предполагая
, и последнее обстоятельство является принципиальным. С самого начала М – это конструкция для приближенного описания объекта и, предполагая  , мы искажаем смысл понятия точно правой части
, мы искажаем смысл понятия точно правой части 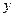 в (42).
в (42).
Если на М решение (42) неединственно, то схема регуляризации вообще нуждается в доработке. Представим, что условие единственности на М выполнено, но существует множество  , и на Х решение уравнения (42) неединственно. Реальное, точное решение принадлежит Х, но лишь приближенно (хотя и с высокой точностью) описывается некоторым элементом из М. Спрашивается, какой смысл приобретает понятия “точная правая часть” в (42) и “точное решение” в этой распространенной в приложениях ситуации. Найдя единственное квазирешение на М, соответствующее реальным входным данным и, получив в результате элемент, лежащий в
, и на Х решение уравнения (42) неединственно. Реальное, точное решение принадлежит Х, но лишь приближенно (хотя и с высокой точностью) описывается некоторым элементом из М. Спрашивается, какой смысл приобретает понятия “точная правая часть” в (42) и “точное решение” в этой распространенной в приложениях ситуации. Найдя единственное квазирешение на М, соответствующее реальным входным данным и, получив в результате элемент, лежащий в 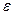 – окрестности гипотетического “точного” решения, соответствующего гипотетической “точной” правой части, мы ничего определенного не можем сказать о его близости к реальному и, следовательно, о степени соответствия полученного квазирешения реальной среде.
– окрестности гипотетического “точного” решения, соответствующего гипотетической “точной” правой части, мы ничего определенного не можем сказать о его близости к реальному и, следовательно, о степени соответствия полученного квазирешения реальной среде.
Сказанное еще раз повторяет тот вывод, к которому мы пришли в гл.3, состоящей в том, что к применению формальных схем регуляризации задачам, имеющим расширение до неединственных, следует относиться исключительно осторожно. Следует для таких задач развивать свои, учитывающие неоднозначность исходных постановок, методы.
Литература
1. Тиханов А.Н., Арсенин В.Я. Методы решения некорректных задач. – М.: Наука, 1979 –285с.
2. Некорректные задачи математической физики и анализа / М.М. Лаврентьев и др. – М.: Наука, 1980. – 286с.
3. Теория линейных некорректных задач и её приложения / В.К. Иванов и др. – М.: Наука, 1978. – 206с.
4. Латтес Р., Лионс Ж-Л. Метод квазиобращения и его приложения. – М.: Мир, 1970. – 336с.
5. Страхов В.Н. О центральной вычислительной задаче гравиметрии, магнитометрии, геодезии и геоинформатики. В сб. «Вопросы теории и практики геологической интерпретации гравитационных, магнитных и электрических полей .Материалы 34-й сессии Международного семинара им. Д.Г. Успенского» Москва ИФЗ РАН 2007, стр. 239-262.
Глава 5. КРИТЕРИАЛЬНЫЕ ПРИНЦИПЫ ДООПРЕДЕЛЕНИЯ ОБРАТНЫХ ЗАДАЧ ГЕОФИЗИКИ.
|
из
5.00
|
Обсуждение в статье: Итерационная регуляризация |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

