 |
Главная |
Глава 6. Эволюционно-динамические модели интегрированной интерпретации
|
из
5.00
|
6.1. Общие рассмотрения.
Использование критериев оптимальности как способа отбора единственного элемента из множества эквивалентных по заданному геофизическому полю составляет физико-математическую основу для постановки обратных задач интегрированной интерпретации. В этой постановке все иные, кроме заданного поля, данные выражены в виде критерия оптимальности, который реализует принцип построения сбалансированных моделей. Отсюда происхождение термина – «интегрированная интерпретация».
Принцип построения сбалансированных моделейдостаточно универсален и очевиден. Он состоит в том, что реконструируемые физико-геологические модели в конечном итоге должны быть сбалансированы относительно всех имеющихся геофизических полей и геомеханических законов. Это означает, в частности, что реконструируемая физико-геологическая модель среды должна иметь соответствующие геофизическим полям содержательные физические модели. Моделируемые физические поля должны соответствовать наблюдаемым. Если моделируемое поле, например, гравитационное, не совпадает в пределах требуемой точности, с наблюдаемым, то плотностная модель самым решительным образом должна быть пересмотрена. Различные содержательные физические модели единой геологической среды должны быть согласованы между собой и отражать различные стороны одного и того же объекта. Если они не согласованы, противоречат друг другу, то следует от них отказаться, и среди им эквивалентных по полю, искать другие, согласованные между собой. Наконец, требование сбалансированности означает, что физико-геологические модели должны быть согласованы с эволюционно–динамических позиций. Они должны иметь согласованные с геомеханическими законами параметры и отражать предполагаемую эволюционно- геодинамическую модель. Каждая структура и каждое образование имеют свой генезис – свое происхождение. В формировании структуры принимало участие множество сил, как внешних – тектонические движения структур более высокого порядка, катастрофические события, так и внутренних, диктуемых законами механики сплошных сред - взаимодействие элементов структуры между собой и окружающими образованиями, что, впрочем, входит составной частью в законы механики сплошных сред. Картину геологического строения можно считать завершенной только тогда, когда помимо согласования со всеми наблюдаемыми физическими полями, она количественно проанализирована с механико-геологических позиций, является непротиворечивой, устойчивой на своих геологических масштабах времени, выяснен ее количественный генезис – породившая ее динамика сил и соответствующая ей динамика перемещений. В этом и состоит принцип сбалансированных моделей в его широком понимании. Однако его конкретная реализация предполагает поэтапную, пометодную балансировку.
Использование введенных выше критериев оптимальности при реконструкции физически содержательной модели обеспечивает корректировку начальной модели – нулевого приближения, являющегося несбалансированной моделью метом минимальных корректив(ММК) по введенному критерию. В этом методе следует выполнить минимальные движения модели нулевого приближения , относительно введенного критерия, до ее сбалансированного по физическому полю аналога. Критерий оптимальности в этих методах определяет направление движения при трансформации начальной модели в процессе ее балансировки[24]. Например, направление балансировки начальной модели может определяться требованием минимальных энергетических потерь при трансформации модели из одного состояния к другому – сбалансированному. Именно такую трактовку можно придать процессам выделения оптимального решения из класса эквивалентных, которые реализованы с помощью итерационных процедур (например, 5.73). Важно отметить то обстоятельство, что в процессе итераций (5.73) критерий оптимальности не изменяется и направление внесения корректив остается в пределах всей процедуры решения обратной задачи неизменным.
В том случае, когда изучаемая физико-геологическая модель должна быть сбалансирована по двум или более физическим полям, направление трансформации модели определено принципами согласованности, близости между собой различных физических моделей единой геологической среды. Например, если требуется, чтобы различные физические модели были наиболее близкими между собой в корреляционном смысле, то направление внесения корректив до получения наиболее согласованной системы моделей определяется критерием наилучшей корреляционной связи, и следующими отсюда квадратичными принципами. Этот процесс реализуется итерационной схемой (5.92), и называется методом комплексных минимальных корректив(МКМК). Он схематично иллюстрируется рис. 1,

Рис. 6.1. Иллюстрация сходимости итерационного процесса для совместногоя решения двух обратных задач – метод комплексных минимальных корректив.  – начальное приближение к первой модели;
– начальное приближение к первой модели;  - очередное j-ое приближение к i-ой модели на различных этапах итерационного процесса;
- очередное j-ое приближение к i-ой модели на различных этапах итерационного процесса;  класс эквивалентных по полю
класс эквивалентных по полю  моделей для первого метода (
моделей для первого метода (  );
);  класс эквивалентных по полю
класс эквивалентных по полю  моделей для второго метода (
моделей для второго метода (  ).Движение осуществляется по направлению, определенному видом критероия оптимальности
).Движение осуществляется по направлению, определенному видом критероия оптимальности  .
.
которым подчеркивается, что сбалансированная модель по комплексу полей на самом деле есть система сбалансированных моделей каждая по своему физическому полю и взаимно увязанная между собой по принципу наилучшего взаимного согласования. Это система, вообще говоря, отличающихся между собой моделей. Балансировочные принципы обеспечивали их максимальную взаимную согласованность. Здесь также важно отметить, что критерий близости в процессе решения задачи внесения комплексных минимальных корректив не изменяется на протяжении решения задачи. Это проявляется в том, что параметры критерия оптимальности в итерационном процессе, как (5.73), так и (5.92) не меняются от шага к шагу итерационного процесса. При этом сам критерий оптимальности, как в ММК, так и МКМК вводится априори. По сути своей, результативность решения обратных задач в значительной степени определяется вводимыми явно, как в критериальных методах, или неявно, как в аппроксимационных, принципами балансировки, и это происходит в тем большей мере, чем выше эквивалентность в общей формулировке для рассматриваемых обратных задач. Нуждается в уточнении сам термин «обратные задачи» - это специфика геофизики. Различие между физическими моделями, до решения обратной задачи и после нее, определено, возможно, в большей мере, критериями оптимальности, являющимися выражением балансировочных правил, чем собственно информацией, заложенной в поле. Эта последняя информация характеризует меру разбалансированности и необходимость внесения дальнейших корректив по правилам балансировки, например, минимальных движений.
Направление трансформации модели от некоторого начального состояния к конечному - это его эволюция, подчиненная тому, либо иному, эволюционному принципу - минимальных энергетических затрат, наилучших корреляций и т.д. Однако эволюционно-динамические принципы трансформации физической модели, от несбалансированной в ее начальном состоянии к сбалансированной в конечном, могут быть введены из геодинамических законов развития изучаемого объекта.
Принцип моделирования динамики развитиягеологического объекта, например, седиментационного бассейна, состоит в реконструкции и моделировании фрагментов его развития, исходя из некоторого начального положения к очередному, при заданных параметрах, определяющих динамику процесса. Геодинамические параметры могут быть заданы априори или уточняться в процессе моделирования. В первом случае, такое моделирование основано на решении уравнений вязкого течения жидкости (уравнений движения Навье - Стокса), конвективных потоков, и одной из главных его целей служит построение генерализованной модели движений, приводящей к современному состоянию объекта, сравнительный анализ сценариев его развития. Для этого следует задать модель среды и перечень геодинамических параметров, определяющих эволюцию системы. Определяющим фактором, влияющим на величину скорости перемещений, служит вязкость. Она определяется из внешних условий – экспериментов, сопоставления скоростей распространения продольных и поперечных сейсмических волн. Однако распределение этого параметра определяется крайне ненадежно. Исключительная зависимость вязкости от слабо поддающихся измерению и учету, и потому, неконтролируемых внешних условий, видна из материалов, приведенных на рис.3.

|
| Рис.2. Зависимость эффективной вязкости толщ горных пород h3 от интенсивности касательных напряжений t при атмосферном давлении и температуре 200 (по материалам Гзовского []). |
I категория – толщи глин, солей, гипсов, тонкослоистых алевролито-глинистых пород; II категория – тонкослоистые известняково-мергелистые, песчано-глинистые, флишевые толщи; III категория – слабослоистые песчаниковые, конгломератовые, карбонатные, вулканогенные, а также в прошлом сильно дислоцированные и слабо метаморфизованные песчано-глинистые толщи; IV категория – граниты и другие интрузивные породы (кроме ультраосновных), гнейсы, кристаллические сланцы. А – область условно-мгновенного разрушения. 1 и 2 – зависимость h от t для гипса при всестороннем давлении 1000 и 1 кг/см2.
Как видно, незначительные изменения величин касательных напряжений, действующих на горную породу, приводит к изменению значений вязкости на порядки, что влечет за собой существенное изменениям скорости течений. Причем коэффициенты вязкости, характеризующие среду, сами зависят от напряжений, что еще более усугубляет неопределенность ситуации.
Второй путь (рис. 3) основан на уточнении геодинамических параметров, в частности, скорости течений на основе требования эволюции реконструируемой модели к сбалансированной, согласованной по геофизическому полю. Этот путь, который называется методом эволюционно–динамического продолжения, в равной степени, следует отнести, как к принципам сбалансированных моделей на основе геодинамических методов, так и принципам моделирования динамики развития объектов.
 Сущность метода эволюционно–динамического продолжения состоит в реконструкции физической модели геологического объекта на основе использования в качестве балансировочных принципов законов его эволюции, регулируемой геодинамическими параметрами от начального времени и начальной модели к настоящему (текущему) состоянию. Требования к геодинамическим параметрам и, тем самым, выбору сценария эволюции, состоят в том, чтобы эволюционирующая модель вела к современным, наблюдаемым физическим полям. Такой подход позволяет соединить процесс реконструкции физической модели с созданием непротиворечивой модели его формирования. Причем управляющие процессом параметры, а это, прежде всего, распределение скоростей движения и характер внешних источников, конструируются как интегральные параметры, объединяющие в себе всю информацию о свойствах изучаемой среды. Таким образом, исходя из заданного начального распределения физического параметра и общих представлений о механизме его трансформации к современному состоянию, может быть смоделирован процесс эволюции.
Сущность метода эволюционно–динамического продолжения состоит в реконструкции физической модели геологического объекта на основе использования в качестве балансировочных принципов законов его эволюции, регулируемой геодинамическими параметрами от начального времени и начальной модели к настоящему (текущему) состоянию. Требования к геодинамическим параметрам и, тем самым, выбору сценария эволюции, состоят в том, чтобы эволюционирующая модель вела к современным, наблюдаемым физическим полям. Такой подход позволяет соединить процесс реконструкции физической модели с созданием непротиворечивой модели его формирования. Причем управляющие процессом параметры, а это, прежде всего, распределение скоростей движения и характер внешних источников, конструируются как интегральные параметры, объединяющие в себе всю информацию о свойствах изучаемой среды. Таким образом, исходя из заданного начального распределения физического параметра и общих представлений о механизме его трансформации к современному состоянию, может быть смоделирован процесс эволюции.
Рассмотрим общие эволюционные уравнения для моделей распределения физического параметра и модели системы границ, разделяющих пласты с заданными свойствами внутри. Предварительно эти вопросы рассматривались в разделе 2.5.
Произвольная величина, имеющая распределение  , движение которой происходит в зависимости от пространственных
, движение которой происходит в зависимости от пространственных  и временной
и временной 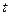 координат, подчиняется основному кинетическому уравнению для любого элемента объема
координат, подчиняется основному кинетическому уравнению для любого элемента объема 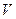 :
:
 .
.
 Здесь
Здесь 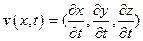 - вектор скорости движений, зависящий, как от пространственных координат, так и от времени
- вектор скорости движений, зависящий, как от пространственных координат, так и от времени  ,
,  - элемент объема:
- элемент объема: 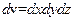 . Если величина
. Если величина  в процессе движения сохраняется, то
в процессе движения сохраняется, то  и
и  . В том случае, если в точке
. В том случае, если в точке  в момент времени
в момент времени 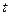 величина
величина  изменяется, и это изменение есть
изменяется, и это изменение есть  , то закон сохранения для
, то закон сохранения для  будет иметь вид:
будет иметь вид:

| (6.1) |
Величина  , входящая в уравнение (1), трактуется как положительные, либо отрицательные внешние источники. Они обеспечивают динамику параметра
, входящая в уравнение (1), трактуется как положительные, либо отрицательные внешние источники. Они обеспечивают динамику параметра  за счет внешнего притока либо оттока вещества. Например, рассматривая в качестве величины
за счет внешнего притока либо оттока вещества. Например, рассматривая в качестве величины  распределение плотности
распределение плотности  , уравнение (1) примет вид закона сохранения:
, уравнение (1) примет вид закона сохранения:
 . .
| (6.2) |
Здесь  ‑ внешние источники масс, ассоциирующиеся с процессами седиментации или притока извне (положительные значения), эрозией, размывом (отрицательные значения). Введение этого параметра достаточно условно. Его истинное значение и физический смысл состоит в том, чтобы в «конечной точке» эволюционирующей системы обеспечить то полное количество вещества, которое соответствует наблюдаемому полю, компенсировать дисбаланс полной массы, существующий в «начальной» модели. Эволюционно-динамическое продолжениезаданной модели
‑ внешние источники масс, ассоциирующиеся с процессами седиментации или притока извне (положительные значения), эрозией, размывом (отрицательные значения). Введение этого параметра достаточно условно. Его истинное значение и физический смысл состоит в том, чтобы в «конечной точке» эволюционирующей системы обеспечить то полное количество вещества, которое соответствует наблюдаемому полю, компенсировать дисбаланс полной массы, существующий в «начальной» модели. Эволюционно-динамическое продолжениезаданной модели  - из начального положения в момент времени
- из начального положения в момент времени 
 к конечному, соответствующему некоторому моменту времени
к конечному, соответствующему некоторому моменту времени  , должно подчиняться требованию, состоящему в том, чтобы окончательная модель должна быть сбалансирована по физическому полю. Это значит, что:
, должно подчиняться требованию, состоящему в том, чтобы окончательная модель должна быть сбалансирована по физическому полю. Это значит, что:
 , ,
| (6.3) |
где  - оператор решения прямой задачи для параметра
- оператор решения прямой задачи для параметра  ,
, 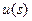 - заданное геофизическое поле – его современное состояние. Требование (3) означает, что окончательная, к моменту времени
- заданное геофизическое поле – его современное состояние. Требование (3) означает, что окончательная, к моменту времени  , модель распределение
, модель распределение 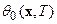 , должна соответствовать интерпретируемому полю. Таким образом, объединяя сформулированные условия, получим задачу эволюционно–динамического продолжения:
, должна соответствовать интерпретируемому полю. Таким образом, объединяя сформулированные условия, получим задачу эволюционно–динамического продолжения:

 ; ;
 . .
| (6.4) |
Механизм эволюции величины  контролируется величиной вектора скорости
контролируется величиной вектора скорости  и законом поступления или оттока вещества, контролируемым функцией для внешних источников
и законом поступления или оттока вещества, контролируемым функцией для внешних источников  , которые следует считать компенсационными параметрами. Если эти параметры заданы, то задача (4) переопределена. Условие (3) в ней излишне. Но эти геодинамические параметры реально никогда точно не известны. В лучшем случае, известны достаточно грубые оценки для их возможных величин – направление, диапазон допустимых значений. Поэтому они должны подбираться и уточняться так, чтобы было выполнено условие (3). В результате задача (4) оказывается непротиворечивой.
, которые следует считать компенсационными параметрами. Если эти параметры заданы, то задача (4) переопределена. Условие (3) в ней излишне. Но эти геодинамические параметры реально никогда точно не известны. В лучшем случае, известны достаточно грубые оценки для их возможных величин – направление, диапазон допустимых значений. Поэтому они должны подбираться и уточняться так, чтобы было выполнено условие (3). В результате задача (4) оказывается непротиворечивой.
Рассмотрим теперь модель эволюции структурных элементов. Эти модели частный, но исключительно важный и распространенный тип рассмотренных выше моделей среды с пространственно распределенными параметрами. Также как и в задачах гравиметрии структурного типа, под структурными моделями понимается геометрическая модель среды, описываемая системой поверхностей, разделяющих некоторые моно-, либо гетерогенные комплексы. Физические свойства внутри этих комплексов, например, плотностные, скоростные известны. Они могут быть постоянны, либо переменны, но принципиально важно, что они заданы. Именно этим отличаются структурные задачи от общих задач реконструкции моделей с распределенными параметрами, в частности, рассмотренных выше моделей распределения параметра  как функции пространственно-временных координат. Необходимо, как и для распределений
как функции пространственно-временных координат. Необходимо, как и для распределений  построить уравнения эволюционирующей системы границ так, чтобы, подчиняясь общим законам движения, контролируемым геодинамическими параметрами, они приводили к сбалансированным, относительно геофизического поля, результатам. Иллюстрация этого принципа приведена на рис. 4.
построить уравнения эволюционирующей системы границ так, чтобы, подчиняясь общим законам движения, контролируемым геодинамическими параметрами, они приводили к сбалансированным, относительно геофизического поля, результатам. Иллюстрация этого принципа приведена на рис. 4.
Предполагаемое первоначальное состояние (верхний разрез) отражает представление о ранних стадиях эволюции фрагмента осадочного бассейна. Рассчитанное от этой модели гравитационное поле существенно отличается от современного. Предполагая тенденцию к погружению фундамента и контролируя скорость перемещения границ по фактору приближения рассчитанного и наблюдаемого поля, последовательно переходим от промежуточной к окончательной модели среды (нижний рисунок).
Модель среды в стационарном состоянии представляет собой систему уравнений для глубин залегания плотностных границ:  в зависимости от горизонтальных координат
в зависимости от горизонтальных координат  , с известным распределением физического параметра
, с известным распределением физического параметра  , например, плотности
, например, плотности  , между ними (см. 2.5). Наиболее распространенный случай, не требующий дополнительных определений в случае изменения конфигурации границ, – это случай постоянных значений параметра, имеющего чаще всего смысл значения параметра эффективного (обобщенного), служащего своего рода идентификатором эволюционирующего элемента рассматриваемого комплекса.
, между ними (см. 2.5). Наиболее распространенный случай, не требующий дополнительных определений в случае изменения конфигурации границ, – это случай постоянных значений параметра, имеющего чаще всего смысл значения параметра эффективного (обобщенного), служащего своего рода идентификатором эволюционирующего элемента рассматриваемого комплекса.
|

Принципиально важно для последующего анализа рассмотрение введенных границ одновременно, как геодинамических так и физических. Геодиномические . эволюционируют в зависимости от внешних воздействий и внутренних геологических свойств, характерных для рассматриваемого региона, а физические – отображаеются в физическом поле 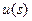 с помощью оператора прямой задачи
с помощью оператора прямой задачи  . Рассматривая процесс эволюции, необходимо к уравнениям границ добавить эволюционный параметр– время t:
. Рассматривая процесс эволюции, необходимо к уравнениям границ добавить эволюционный параметр– время t:  . Сама эволюция начинается с нулевого момента времени и некоторой начальной модели
. Сама эволюция начинается с нулевого момента времени и некоторой начальной модели  и продолжается до «момента времени»
и продолжается до «момента времени»  , заканчиваясь состоянием
, заканчиваясь состоянием  .
.
Структурные геодинамические модели и уравнения, описывающие их эволюцию, рассматривались в разделе 2.5. Там приведена и начальная библиография по вопросу. Напомним, что для того, чтобы получить уравнение эволюционирующей границыиз общего уравнения (2) следует определить понятие внутренних границ. Граница - это сохраняющаяся в процессе эволюции компонента, которая меняет свою форму, поднимается, либо опускается, но остается границей раздела для заданных физических параметров. Это означает, что в процессе эволюции движение вещества через границу не происходит, и она определяется как поверхность, через которую отсутствует поток вещества – параметра  . Следовательно, для каждой из границ системы
. Следовательно, для каждой из границ системы  полная производная по времени для частиц, расположенных на этой поверхности, равна нулю:
полная производная по времени для частиц, расположенных на этой поверхности, равна нулю:  , а последняя, в свою очередь, складывается из производных по времени к пространственной нормальной и частной по времени производных. Это приводит к уравнению движения:
, а последняя, в свою очередь, складывается из производных по времени к пространственной нормальной и частной по времени производных. Это приводит к уравнению движения:
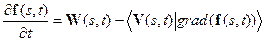 ; ;
 . .
|
Здесь  - начальное положение границ, с которого «начинается» эволюция.
- начальное положение границ, с которого «начинается» эволюция.  ;
;  - управляющие геодинамические параметры, имеющие смысл соответственно вертикальной и горизонтальной составляющих вектора скорости перемещения для каждой из границ.
- управляющие геодинамические параметры, имеющие смысл соответственно вертикальной и горизонтальной составляющих вектора скорости перемещения для каждой из границ.
В дополнение к движениям материала с теми, либо иными, векторами скорости происходит разрушение, переотложение терригенного материала, слагающего изучаемые массивы, что называется денудацией рельефа границ и поступление дополнительного материала из источников вне области рассматриваемых границ – процесс осадконакопления. Дополнительный учет членов, ответственных за денудацию и осадконакопление в процессе эволюции границ (см. цитированную ранее в гл. 2 работу Михайлова В.О. и др. [2.7]), приводит к уравнениям:
 ; ;
 . .
| (6.5) |
Здесь  - оператор, ответственный за модель денудации рельефа;
- оператор, ответственный за модель денудации рельефа;  - сложная векторнозначная функция, ответственная за дивергентную компоненту(привнесение дополнительного материала) в эволюции каждой из границ системы, и определяемая особенностями процессов осадконакопления и метаморфизма. Она зависит от большого числа факторов, включая геологические свойства пород. Однако, именно в силу сложности, равнозначной многофакторности, среди которых нельзя выделить главные, эту компоненту следует рассматривать как отдельное аддитивное слагаемое, определяемое по результатам соответствия, моделирования динамических процессов и сопоставления результатов с наблюдаемыми физическими полями. Ее можно объединить с вертикальной компонентой скорости движения границы и считать ответственной за ее вертикальные движения.
- сложная векторнозначная функция, ответственная за дивергентную компоненту(привнесение дополнительного материала) в эволюции каждой из границ системы, и определяемая особенностями процессов осадконакопления и метаморфизма. Она зависит от большого числа факторов, включая геологические свойства пород. Однако, именно в силу сложности, равнозначной многофакторности, среди которых нельзя выделить главные, эту компоненту следует рассматривать как отдельное аддитивное слагаемое, определяемое по результатам соответствия, моделирования динамических процессов и сопоставления результатов с наблюдаемыми физическими полями. Ее можно объединить с вертикальной компонентой скорости движения границы и считать ответственной за ее вертикальные движения.
Анализ модели формирования структур показывает, что любая произвольная по рельефу слоев структура может быть получена за счет чисто вертикальных движений, с включением дивергентного члена, а при дополнительно заданных внутренних напряжениях, сочетанием дивергентных членов, вертикальных и горизонтальных движений, при том бесконечным множеством способов. Это означает, что процесс денудации может быть включен в дивергентный член, ответственный за характер осадконакопления и метаморфизма, и по характеру своего влияния, на поведение модели в рамках (5), объединен с вертикальной компонентой действующих нагрузок. В этом случае может быть введена интегрированная математическая модель эволюции структур:

 . .
|
Смысл интегрированного параметра  аналогичен тому, какой имеет и величина
аналогичен тому, какой имеет и величина  в эволюционном уравнении (1). Это прирост изучаемой компоненты – в данном случае, вертикальное приращение, которое получает граница за счет суммарных факторов. Также как и в задаче об эволюции распределения параметра, модель эволюции системы границ должна быть доопределена условием, чтобы процесс эволюции вел к заданным, «современным» физическим полям. Это означает дополнительное введение требования:
в эволюционном уравнении (1). Это прирост изучаемой компоненты – в данном случае, вертикальное приращение, которое получает граница за счет суммарных факторов. Также как и в задаче об эволюции распределения параметра, модель эволюции системы границ должна быть доопределена условием, чтобы процесс эволюции вел к заданным, «современным» физическим полям. Это означает дополнительное введение требования:
 , ,
|
Это требование уточняет величины и снижает неопределенность в значениях управляющих геодинамических параметров. Окончательно, задача эволюционно-динамического продолжения для системы границ формулируется следующим образом:


 . .
| (6.6) |
Уравнения (4) и (6) служат исходными для методов эволюционно-динамического продолжения при эволюционно-динамическом интегрированном анализе геолого–геофизических данных.
|
из
5.00
|
Обсуждение в статье: Глава 6. Эволюционно-динамические модели интегрированной интерпретации |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

