 |
Главная |
Вычислительная схемас использованием спектральной формы решения обратной задачи структурной гравиметрии на экстремальных классах
|
из
5.00
|
Соотношением (92) определен неограниченный оператор. Это полностью аналогичное (42) соотношение для устойчивого вычисления значения которого, следует пользоваться методами теории регуляризации. Применим для решения этой задачи приемы, развитые для устойчивого вычисления (42). Это оправдано в силу близости между собой этих задач.
Перепишем выражение для решения (92) в форме:
 (7.95)
(7.95)
 (7.96)
(7.96)
Спектр функций, входящих в (95, 96) будем вычислять с помощью дискретного преобразования Фурье (ДПФ).


Здесь 
Используются те же обозначения, что и для рассмотренной выше задачи о распределении плотности.
Пусть

Обозначим  область ненулевых коэффициентов Фурье функций
область ненулевых коэффициентов Фурье функций  ,
, 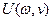 ,
,  .
.
Введем обозначения


 (7.97)
(7.97)
 .
.
Далее, будем рассматривать нормы:
 . (7.98)
. (7.98)
Теперь можно записать:

Следовательно, норма оператора (97) ограничена величиной  . Далее, уклонение
. Далее, уклонение  от
от  , соответствующего решению
, соответствующего решению  :
:
 ,
,
вычисляется следующим образом:

Тогда
 .
.
Следовательно, выбор  из условия:
из условия:
 , (7.99)
, (7.99)
обеспечивает согласованность погрешности, с которой задано  (в смысле (98)), и величины параметра регуляризации
(в смысле (98)), и величины параметра регуляризации  .
.
Далее, так же, как и в задаче, для выделения решения в классе распределений плотности при выборе параметра  следует учитывать два, в общем, противоречивых обстоятельства. С одной стороны, увеличение
следует учитывать два, в общем, противоречивых обстоятельства. С одной стороны, увеличение  приводит к повышению устойчивости решения. Оценка для
приводит к повышению устойчивости решения. Оценка для  из (99), обеспечивая заданную величину невязки, может не обеспечивать требуемую устойчивость, и наоборот. Фактически это означает лишь то, что регуляризующее слагаемое в знаменателе
из (99), обеспечивая заданную величину невязки, может не обеспечивать требуемую устойчивость, и наоборот. Фактически это означает лишь то, что регуляризующее слагаемое в знаменателе  выбрано не лучшим образом. Для обеспечения заданного типа устойчивости и минимизации невязки воспользуемся итерационным процессом:
выбрано не лучшим образом. Для обеспечения заданного типа устойчивости и минимизации невязки воспользуемся итерационным процессом:

 (7.100)
(7.100)
где 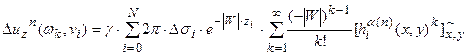 (7.101)
(7.101)
- рассчитанное поле от регуляризованного, с параметром регуляризации 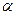 , приближением на
, приближением на 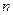 -ом шаге итерационного процесса.
-ом шаге итерационного процесса.
Пусть  Тогда, повторяя рассуждения приведенные получении оценок (59) и (60) получим, что процесс (100) сходится к элементу из
Тогда, повторяя рассуждения приведенные получении оценок (59) и (60) получим, что процесс (100) сходится к элементу из  [34] с гравитационным эффектом, равным
[34] с гравитационным эффектом, равным  , причем:
, причем:
 (7.102)
(7.102)
 (7.103)
(7.103)
Приведем двухмерные аналогивыведенных соотношений для решения в спектральной форме обратной задачи структурной гравиметрии. Напомним (см. гл. 2.1.3) , что двухмерные аналоги – это случай, когда параметры среды и, следовательно, поля не зависят от одной из горизонтальных координат, например, от координаты 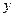 . В этом случае, соотношение между параметрами среды и полем интегрируется в бесконечных пределах по оси
. В этом случае, соотношение между параметрами среды и полем интегрируется в бесконечных пределах по оси  . Модели рассматриваются в сечении плоскостью
. Модели рассматриваются в сечении плоскостью  и все уравнения не зависят от этой координаты. Следует понимать, что речь идет не о «разрезанной в плоскости
и все уравнения не зависят от этой координаты. Следует понимать, что речь идет не о «разрезанной в плоскости  произвольной трехмерной модели, а именно о трехмерной модели, все сечения которой любой из плоскостей
произвольной трехмерной модели, а именно о трехмерной модели, все сечения которой любой из плоскостей  совпадают между собой и дают исчерпывающее представление обо всей модели. Связь между конфигурацией плотностных границ и интерпретируемой компонентой поля задана соотношением:
совпадают между собой и дают исчерпывающее представление обо всей модели. Связь между конфигурацией плотностных границ и интерпретируемой компонентой поля задана соотношением:

которое обозначаем  , или
, или  , если поле задано на горизонтальной линии – оси
, если поле задано на горизонтальной линии – оси  , которую также будем обозначать
, которую также будем обозначать 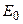 . Аналогом критерия оптимальности (75) будет
. Аналогом критерия оптимальности (75) будет

Представлением решения этой задачи и элементом из экстремального класса  будет
будет
 ,
,
где  непрерывная функция, одна и та же для всех
непрерывная функция, одна и та же для всех  . Теоретическая формула для решения имеет вид:
. Теоретическая формула для решения имеет вид:
 .
.
В спектральной форме прямая задача рассчитывается по формуле:

Итерационный процесс для решения, аналогичный (100) записывается так:

| (7.104) |

| (7.105) |
|
из
5.00
|
Обсуждение в статье: Вычислительная схемас использованием спектральной формы решения обратной задачи структурной гравиметрии на экстремальных классах |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

