 |
Главная |
Приложение 3. Непрерывные группы и их представления
|
из
5.00
|
Есть довольно много веских причин для того, чтобы внимательно изучить те следствия, которые проистекают от факта симметрии объектов относительно некоторых движений в пространстве, или более обще – некоторых типов преобразований. Одна из них состоит в том, что симметрия связана с законом сохранения в физике. Собственно это и понятно. Если под действием преобразования нечто не изменяется – т.е. симметрично относительно этого преобразования, то по другому это произносится – нечто сохраняется при преобразованиях. Например, с течением времени не меняется полная энергия системы – система симметрична относительно преобразований сдвига по времени. Оказывается, однако, что сам факт записи дифференциальных уравнений часто означает ничего иного, как перечень минимального числа тех преобразований, которым подвергаются начальные данные этого уравнения. Но отсюда возможны и алгоритмические следствия – проще моделировать сами эти движения, чем искать сеточными или иными приемами решения дифференциальных уравнений. Результат один и тот же, но достигается разными по трудоемкости и прозрачности средствами. Понятие движения подразумевает нечто, непрерывно связанное с некоторым параметром, например, временем, хотя это не единственный и даже не лучший параметр. Например, роль такого параметра может играть пространственная координата или некоторый формальный параметр.
Другая веская причина рассмотрения симметрий - специфическая для геофизических методов исследования неоднородных сред. Она состоит в том, что факт симметрии какого- либо процесса или явления в пространстве времени свидетельствует и воспринимается как однородность пространственно–временного многообразия относительно этого процесса. Наоборот, неоднородности среды воспринимаются как неоднородности лишь постольку, и в том объеме, поскольку и как рельефно проявляются в виде нарушения симметрии распространения в пространственно–временном многообразии физического поля. Поскольку геофизические методы направлены на изучение неоднородностей среды, то локальные нарушения симметрий – их основной предмет изучения.
Группой(преобразований, действующих на некотором пространстве) называется такое множество 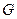 ,
,
для каждых двух элементов  и
и  которой определено понятие их композиции
которой определено понятие их композиции 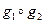 (умножения, последовательного применения), так что результат композиции есть снова элемент из
(умножения, последовательного применения), так что результат композиции есть снова элемент из 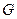
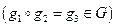 .
.
Существует единичный элемент  е со свойством:
е со свойством:  .
.
Для каждого элемента g из G существует принадлежащий G элемент  , называемый обратным к g, такой, что:
, называемый обратным к g, такой, что: 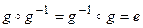 .[40]
.[40]
Непрерывной группойназывается множество 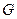 , элементы которого есть непрерывные функции параметра
, элементы которого есть непрерывные функции параметра 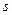 со значении в некотором пространстве
со значении в некотором пространстве  . Для того, чтобы это сделать, надо, как минимум, ввести на множестве
. Для того, чтобы это сделать, надо, как минимум, ввести на множестве  топологии или метрику, а лучше норму[41], и показать, что любые два элемента
топологии или метрику, а лучше норму[41], и показать, что любые два элемента  группы
группы 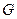 соответствуют значениям параметра
соответствуют значениям параметра  и
и  , и их можно непрерывным образом соединить, двигаясь по кривой соединяющей точки
, и их можно непрерывным образом соединить, двигаясь по кривой соединяющей точки  и
и  в
в  . Понятие непрерывной группы может быть введено и исследовано в самых общих предположениях. Это красивая, содержательная теория. Однако далее для иллюстративных целей вполне достаточно иметь аналоги пространственно-временных трансформаций (понятия трансформации и преобразования являются синонимами), куда относятся: сдвиги (трансляции), вращения, растяжения-сжатия. Другой тип преобразований дают преобразование зеркального отражения. Они не является непрерывным. Действительно, нельзя отразиться в бесконечном зеркале наполовину или, скажем, на две трети. Несмотря на это, преобразование играет большую роль при классификации непрерывных пространственно-временных трансформаций. Подгруппой группы
. Понятие непрерывной группы может быть введено и исследовано в самых общих предположениях. Это красивая, содержательная теория. Однако далее для иллюстративных целей вполне достаточно иметь аналоги пространственно-временных трансформаций (понятия трансформации и преобразования являются синонимами), куда относятся: сдвиги (трансляции), вращения, растяжения-сжатия. Другой тип преобразований дают преобразование зеркального отражения. Они не является непрерывным. Действительно, нельзя отразиться в бесконечном зеркале наполовину или, скажем, на две трети. Несмотря на это, преобразование играет большую роль при классификации непрерывных пространственно-временных трансформаций. Подгруппой группы 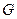 называется подмножество
называется подмножество  в
в 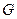 , обладающее всеми свойствами группы
, обладающее всеми свойствами группы 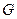 и замкнутое относительно групповой операции. Последнее означает, что для любых двух элементов из
и замкнутое относительно групповой операции. Последнее означает, что для любых двух элементов из  , их произведения и обратные элементы принадлежат
, их произведения и обратные элементы принадлежат  .
.
Пусть на пространстве  осуществлено линейное преобразование, сохраняющее длины всех векторов. Это преобразование от координат
осуществлено линейное преобразование, сохраняющее длины всех векторов. Это преобразование от координат  к координатам
к координатам  задается соотношением[42]:
задается соотношением[42]:
 (1)
(1)
Здесь  - компоненты матрицы, характеризующей преобразование,
- компоненты матрицы, характеризующей преобразование,  - компоненты характеризующие вектор сдвига.
- компоненты характеризующие вектор сдвига.
Используется правило суммирования Эйнштейна, в соответствии с которым по дважды повторяющемся индексу происходит суммирование. Если индекс греческий, суммирование происходит от 0 до 3; если индекс латинский – от 1 до 3. Мы не следим за балансом нижних и верхних индексов, используя только нижние, только верхние, или те, и иные, лишь из соображений удобства письма. Поскольку длина векторов при преобразованиях остается неизменной, то исключая сдвиг получим:  и, следовательно:
и, следовательно:

Как обычно, через  обозначен символ Кронекера– дискретный аналог дельта импульса Дирака.
обозначен символ Кронекера– дискретный аналог дельта импульса Дирака. 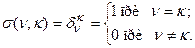
Поскольку  то матрица
то матрица  ортогональна и
ортогональна и  . Следовательно, типы преобразования, осуществляемые матрицей
. Следовательно, типы преобразования, осуществляемые матрицей  , разбиваются на два класса: с положительным и отрицательным детерминантом. Их совокупность обозначается O(4). Ту их часть, которая обладает положительным единичным детерминантом, обозначим SO(4). Понятно, что SO(4)есть подгруппа в O(4). Часть преобразования (1), связанную со смещением вектора
, разбиваются на два класса: с положительным и отрицательным детерминантом. Их совокупность обозначается O(4). Ту их часть, которая обладает положительным единичным детерминантом, обозначим SO(4). Понятно, что SO(4)есть подгруппа в O(4). Часть преобразования (1), связанную со смещением вектора  на вектор
на вектор  , с компонентами
, с компонентами  обозначим Т(4). Эта подгруппа группы преобразований (1) (но не подгруппа в O(4)) называется подгруппой трансляций рассматриваемой группы преобразований.
обозначим Т(4). Эта подгруппа группы преобразований (1) (но не подгруппа в O(4)) называется подгруппой трансляций рассматриваемой группы преобразований.
Введенные преобразования являются непрерывными. Это следует понимать в том смысле, что какое бы из рассматриваемых преобразований не было бы осуществлено, можно осуществить и другое, сколь угодно близкое к нему. Для каждой из таких непрерывных групп преобразований полезно ввести понятие связанного с ней множества, бесконечно близких к единичному, преобразований. Это даст возможность описывать преобразования бесконечно близкие к заданному. Опишем это множество.
Сдвиг по координате  на величину
на величину  описывается самой величиной
описывается самой величиной  . Таким образом, для Т(4), бесконечно близкое к единичному, преобразование описывается так:
. Таким образом, для Т(4), бесконечно близкое к единичному, преобразование описывается так:
 ,
,
где  .
.
Рассмотрим теперь бесконечно малые преобразования для S0(4). Преобразования, бесконечно близкие к единичному, могут быть описаны с помощью суммы единичной матрицы  , оставляющей вектор
, оставляющей вектор  без изменений, и матрицы с компонентами
без изменений, и матрицы с компонентами  , обеспечивающей бесконечно малое преобразование вектора
, обеспечивающей бесконечно малое преобразование вектора  . Тогда преобразование из окрестности единицы задается условием:
. Тогда преобразование из окрестности единицы задается условием:
 .
.
Длина результирующего вектора легко вычисляется:
 +члены квадратичные по
+члены квадратичные по  .
.
Пренебрегая квадратичными членами, в силу их малости, получаем из условия равенства длин исходного и преобразованного векторов, что матрица  кососимметрична:
кососимметрична:
 .
.
Действительно, из 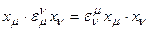 следует
следует  =
= 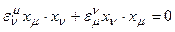 при
при  .
.
Таким образом, только 6 независимых параметров характеризуют бесконечно малое преобразование на SO(4), причем, само это преобразование задается кососимметричной матрицей. Её определитель, равен нулю, поскольку диагональные элементы кососимметричной матрицы тождественно равны нулю.
Общее число параметров, характеризующих преобразование векторов в четырехмерном пространстве (пространстве-времени) без изменения их длин и сохранения ориентации (определитель положителен) оказывается равным десяти. Оно складывается из вращений, характеризуемых шестью независимыми параметрами кососиметричной матрицы и трансляций, характеризуемых четырьмя параметрами. Легко убедиться в том, что эти преобразования образуют непрерывную группу.
Действительно, групповые свойства для каждого из множеств преобразований SО(4) и Т(4) очевидны:
1. Определена операция умножения (композиции двух преобразований). Произведение (последовательное применение) двух преобразований из этого множества преобразований дает новое преобразование из того же множества;
2. Существует единичное преобразование (единичная матрица  ), умножение на которое не меняет преобразования;
), умножение на которое не меняет преобразования;
3. Для каждого преобразования существует ему обратное из того же множества.
Непрерывность следует из того, что поворот может быть осуществлен на какой угодно малый угол, а сдвиг - на любую сколь угодно малую величину.
Непрерывная группа(полугруппа) называется группой(полугруппой) Ли.
Рассмотрим способ нахождения бесконечно малых преобразований из заданной непрерывной группы. Пусть преобразование  из группы g непрерывно зависит (строго говоря, группа g должна быть топологической2 для того, чтобы имело смысл понятие непрерывности) от вектора параметров
из группы g непрерывно зависит (строго говоря, группа g должна быть топологической2 для того, чтобы имело смысл понятие непрерывности) от вектора параметров  , размерность которого N. Таким образом,
, размерность которого N. Таким образом,  есть функция s:
есть функция s:  . Бесконечно малое преобразование (дифференциал, инфинитезимальное преобразование) из g можно определить так:
. Бесконечно малое преобразование (дифференциал, инфинитезимальное преобразование) из g можно определить так:
 .
.
Оператор 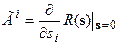 называется генератором бесконечно малого преобразования, или производящим оператором.
называется генератором бесконечно малого преобразования, или производящим оператором.
Результатом действия бесконечно малого преобразования из g на вектор x вычисляется по формуле:
 . (2)
. (2)
Оператор  , применяемый к вектору
, применяемый к вектору  , характеризует собственно операцию бесконечно малого преобразования, называется инфинитезимальным оператором группы (полугруппы). Таким образом, оператор бесконечно малого преобразования "раскладывается" в набор генераторов по каждому из параметров, характеризующих преобразование из группы Ли, и вариации самих этих параметров.
, характеризует собственно операцию бесконечно малого преобразования, называется инфинитезимальным оператором группы (полугруппы). Таким образом, оператор бесконечно малого преобразования "раскладывается" в набор генераторов по каждому из параметров, характеризующих преобразование из группы Ли, и вариации самих этих параметров.
Поскольку  - это вектор, то каждый из операторов
- это вектор, то каждый из операторов  - это двухиндексная матрица
- это двухиндексная матрица  . Следовательно, в покомпонентной записи соотношение (2) можно переписать:
. Следовательно, в покомпонентной записи соотношение (2) можно переписать:
 (3)
(3)
Исходя из выясненных ранее свойств бесконечно малого преобразования, задаваемого матрицей  , приходим к выводу о том, что генераторы
, приходим к выводу о том, что генераторы  антисимметричны по индексам {
антисимметричны по индексам {  }. Рассмотрим их явное выражение для введенных выше групп.
}. Рассмотрим их явное выражение для введенных выше групп.
Для подгруппы трансляций легко получить:

Рассмотрим теперь подгруппу вращений. Как было выяснено ранее, она - шестипараметрическая. Выберем в качестве параметров шесть углов поворота в плоскостях:  соответственно. Вращения в плоскостях, содержащих временную компоненту хо, физически означают переход к движущейся в направлении соответствующей пространственной координаты системе координат. Угол поворота выражается через скорость этого движения. Таким образом, подгруппа четырехмерных вращений имеет собственную подгруппу вращений в трехмерном пространстве и подгруппу движений в трехмерном пространстве.
соответственно. Вращения в плоскостях, содержащих временную компоненту хо, физически означают переход к движущейся в направлении соответствующей пространственной координаты системе координат. Угол поворота выражается через скорость этого движения. Таким образом, подгруппа четырехмерных вращений имеет собственную подгруппу вращений в трехмерном пространстве и подгруппу движений в трехмерном пространстве.
Рассмотрим подгруппу трехмерных вращений. Она состоит из подгруппы S0(3), которую можно назвать чистыми вращениями, и пространственных отражений: 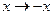 . Поворот вокруг оси
. Поворот вокруг оси  на угол Q задается в трехмерном пространстве соотношением:
на угол Q задается в трехмерном пространстве соотношением:
 .
.
В его справедливости легко убедиться прямым вычислением.
Тогда для генератора  имеем:
имеем:
 . (4а)
. (4а)
Аналогично, имеем для генераторов поворота вокруг осей  и
и  соответственно:
соответственно:
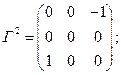
 (4b)
(4b)
Эти матрицы легко переписать и для случая пространственного вращения четырехмерных векторов. Для этого достаточно дописать в них нулевую 4-строку и нулевой 4-столбец.
Генераторы группы Лиимеют не одну групповую операцию, а две. Добавляется аддитивная операция - сложение генераторов. Такого сорта объекты называются алгебрами. Точнее говоря, множество, для элементов которого определены две групповых операции: аддитивная, относительно которой она является группой, и мультипликативная, относительно которой он является полугруппой, (выполняются все условия группы, кроме существования для любого элемента ему обратного в том же множестве) называется алгеброй. Таким образом, набор генераторов, соответствующих группе Ли, образует алгебру. Она называется алгеброй Ли, соответствующей группы Ли. Однако это специфическая алгебра. Аддитивной операцией в ней служит, как уже указывалось, сложение. Что касается умножения (композиции, мультипликативной операции), то оно имеет более сложный характер.
Если ввести на множестве генераторов группы Ли умножение по соответствующему правилу матричного умножения (унаследованного от исходной группы Ли, элементами которой являются и элементы ее алгебры Ли), то получаемый в результате элемент может и не принадлежать алгебре Ли генераторов группы. Иными словами, матричное умножение двух генераторов дает элемент группы, но он может оказаться не соответствующим ни одному из генераторов групп Ли. Для того чтобы превратить множество генераторов в группу Ли относительно мультипликативной операции, примем в качестве последней антикоммутатор, который называется также скобкой Пуассонаили скобочным умножением:
 .
.
Введение такой мультипликативной операции превращает группу Ли генераторов в алгебру Ли. Применение скобочного умножения, в отличие от обычного матричного, не выводит за пределы алгебры, поскольку справедливо следующее равенство:
 .Оно называется коммутационным соотношением. Величины
.Оно называется коммутационным соотношением. Величины  называются структурными константами алгебры Ли. По сути, структурные константы - это самое главное, что определяет собственно алгебраические свойства рассматриваемых объектов. Возможно существование различных по природе объектов, образующих алгебры с одними и теми же структурными константами. В таком случае говорят о различных представлениях одной и той же алгебры Ли. Скобочное умножение
называются структурными константами алгебры Ли. По сути, структурные константы - это самое главное, что определяет собственно алгебраические свойства рассматриваемых объектов. Возможно существование различных по природе объектов, образующих алгебры с одними и теми же структурными константами. В таком случае говорят о различных представлениях одной и той же алгебры Ли. Скобочное умножение  антисимметрично по сомножителям f, d, линейно по каждому множителю и, кроме того, удовлетворяет тождеству Якоби:
антисимметрично по сомножителям f, d, линейно по каждому множителю и, кроме того, удовлетворяет тождеству Якоби:  .
.
 (5)
(5)
Отсюда, в частности, видно, что скобочное умножение в общем случае и неассоциативно. Это означает, что  .
.
Тождество Якоби легко проверяется прямым вычислением, а по форме оно аналогично правилу дифференцирования произведения. Действительно, определим производную элемента f по элементу  правилом
правилом  . Тогда тождество Якоби записывается так:
. Тогда тождество Якоби записывается так:  Последнюю запись можно раскрыть:
Последнюю запись можно раскрыть:
 ,
,
и она с учетом антисимметрии скобочной операции эквивалентна тождеству Якоби.
Для генераторов пространственных вращений структурные константы образуют полностью антисимметричный тензор третьего ранга  с компонентами, равными +1, в случае, если
с компонентами, равными +1, в случае, если 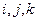 есть четная перестановка чисел1, 2, 3; -1 - в случае нечетной перестановки, нулю - в остальных случаях: [
есть четная перестановка чисел1, 2, 3; -1 - в случае нечетной перестановки, нулю - в остальных случаях: [ 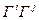 ]= - Гk для
]= - Гk для 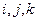 =1, 2, 3; 2, 3, 1; 3, 1, 2 соответственно.
=1, 2, 3; 2, 3, 1; 3, 1, 2 соответственно.
Вращение на бесконечно малый угол 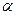 вокруг оси
вокруг оси  задается оператором
задается оператором  Вращение вектора
Вращение вектора  на конечный угол Q можно рассмотреть как результат N поворотов на угол Q/N. Тогда, переходя к пределу для вычисления конечных вращений через найденные выражения для генераторов вращений вокруг соответствующих осей, получим:
на конечный угол Q можно рассмотреть как результат N поворотов на угол Q/N. Тогда, переходя к пределу для вычисления конечных вращений через найденные выражения для генераторов вращений вокруг соответствующих осей, получим:
 (5)
(5)
Алгебра генераторов Ли группы обозначается так же, как и исходная группа Ли, с добавлением впереди буквы А. Например, алгебра Ли группы S0(3) обозначается ASO(3).
Если на множестве, в котором действует группа координатных преобразований g, задана функция  , то под действием этих преобразований происходит изменение функции
, то под действием этих преобразований происходит изменение функции  . Каждому преобразованию
. Каждому преобразованию  можно поставить в соответствие преобразование
можно поставить в соответствие преобразование 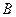 над функциями
над функциями  . Сделать это можно многими разными способами. Потребуем, чтобы преобразования
. Сделать это можно многими разными способами. Потребуем, чтобы преобразования 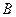 образовывали группу, изоморфную g.
образовывали группу, изоморфную g.
Напомним, что две алгебры, а более обще, и группы, называются изоморфными, если между их элементами существует взаимнооднозначное соответствие, устанавливаемое некоторым отображением, при котором сохраняются групповые соотношения между прообразами и образами при этом отображении. Точнее говоря, если  и
и  группы и
группы и  взаимнооднозначное и непрерывное отображение
взаимнооднозначное и непрерывное отображение  в
в  , то
, то  и
и  изоморфны, если
изоморфны, если  . Если
. Если 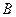 отображение, ставящее в соответствие функции
отображение, ставящее в соответствие функции  некоторую другую функцию того же класса, то этому преобразованию можно поставить в соответствие элемент
некоторую другую функцию того же класса, то этому преобразованию можно поставить в соответствие элемент  из группы
из группы  преобразований векторов по правилу:
преобразований векторов по правилу:
 (6)
(6)
Действительно, правило (6) ставит в соответствие каждому элементу  группы
группы  свой оператор
свой оператор  , действующий на пространстве функций от векторов
, действующий на пространстве функций от векторов  . Это физически разумное правило означает равенство старой и преобразованной функции в одной и той же физической точке. Использование для определения операторов элементов
. Это физически разумное правило означает равенство старой и преобразованной функции в одной и той же физической точке. Использование для определения операторов элементов  , а не R, обеспечивает выполнение групповых свойств для множества операторов.
, а не R, обеспечивает выполнение групповых свойств для множества операторов.
Поясним последнее обстоятельство.
Пусть вслед за оператором  действует оператор
действует оператор  . Тогда
. Тогда  . Соответствие последовательности применения операторов в определении отображения достигнуто.
. Соответствие последовательности применения операторов в определении отображения достигнуто.
Совокупность операторов  , определенных таким образом, образует группу G, называемую представлением группыg на пространстве функций. Являясь представлением на пространстве функций группы Ли, G сама является группой Ли и, следовательно, состоит из операторов B(s), зависящих непрерывно от параметра s. В таком случае G обладает алгеброй Ли AG, находящейся в соответствии с Ag.
, определенных таким образом, образует группу G, называемую представлением группыg на пространстве функций. Являясь представлением на пространстве функций группы Ли, G сама является группой Ли и, следовательно, состоит из операторов B(s), зависящих непрерывно от параметра s. В таком случае G обладает алгеброй Ли AG, находящейся в соответствии с Ag.
Группа Ли G состоит из операторов B(s), непрерывно зависящих от параметра s. Она и исчерпывается этими операторами. Поэтому эквивалентным обозначением для оператора В из G будет G(s). Группой Ли можно назвать и семейство B(s). To же самое можно сказать, и о операторах R, и группе g: R(s) - это группа Ли, a g(s) - ее элемент. Из контекста всегда ясно, о чемидет речь, и путаница здесь исключена.
Воспользуемся определением (6) и найдем элементы алгебры Ли AG, действующей на пространстве дифференцируемых функций и соответствующей генераторам Гi трехмерных вращений (в трехмерном пространстве  ):
):
 (7)
(7)
.
Теперь необходимо воспользоваться правилом  для нахождения генераторов преобразования (7). Принимая во внимание вид операторов Гi,определенных матрицами (4), нетрудно получить:
для нахождения генераторов преобразования (7). Принимая во внимание вид операторов Гi,определенных матрицами (4), нетрудно получить:
 (8)
(8)
Здесь 
Прямым вычислением можно убедиться в том, что полученные генераторы  удовлетворяют тем же коммутационным соотношениям, т.е. имеют те же структурные константы, что и операторы Гi. Следовательно, формулы (8) дают иное представление той же алгебры Ли пространственных вращений. Представление на пространстве дифференцируемых функций. Точно так же легко получить выражения для генераторов группычетырехмерных трансляций в представлении на пространстве дифференцируемых функций в четырехмерном пространстве. Эти генераторы - не что иное, как введенные выше операторы
удовлетворяют тем же коммутационным соотношениям, т.е. имеют те же структурные константы, что и операторы Гi. Следовательно, формулы (8) дают иное представление той же алгебры Ли пространственных вращений. Представление на пространстве дифференцируемых функций. Точно так же легко получить выражения для генераторов группычетырехмерных трансляций в представлении на пространстве дифференцируемых функций в четырехмерном пространстве. Эти генераторы - не что иное, как введенные выше операторы  дифференцирования по координате
дифференцирования по координате  .
.
Так же, как и в (5), вычисление конечных вращений вокруг оси  на угол Q задается оператором:
на угол Q задается оператором:
 .
.
Сдвиг в направлении оси  на величину
на величину  задается оператором:
задается оператором:
 .[43]
.[43]
.
Еще один, очень важный пример группы трансформаций на пространственно-временном многообразии доставляют преобразования дилатации. Преобразования дилатацииD координат  состоят в домножении всех (или оговоренной части) компонент на одно и то же число s.
состоят в домножении всех (или оговоренной части) компонент на одно и то же число s.  Роль нулевого элемента (нулевого угла поворота, сдвига на нулевой вектор) играет значение
Роль нулевого элемента (нулевого угла поворота, сдвига на нулевой вектор) играет значение  . Это одномерная группа Ли, и ее представление на пространстве дифференцируемых функций в качестве своего генератора имеет оператор
. Это одномерная группа Ли, и ее представление на пространстве дифференцируемых функций в качестве своего генератора имеет оператор  . Действительно,
. Действительно,  Таким образом, алгебра Ли одномерна. Индекс i в приведенной выше формуле пробегает значения 1, 2, 3 и тогда речь идет о пространственной дилатации. Если заменить индекс i на греческий, который принимает значения 0, 1, 2, 3, то будет получен генератор пространственно-временной дилатации.
Таким образом, алгебра Ли одномерна. Индекс i в приведенной выше формуле пробегает значения 1, 2, 3 и тогда речь идет о пространственной дилатации. Если заменить индекс i на греческий, который принимает значения 0, 1, 2, 3, то будет получен генератор пространственно-временной дилатации.
Если однопараметрическая группа Ли gимеет генератор Г, то подгруппа  изоморфна g, однако, вообще говоря, с ней не совпадает. Таким образом, легко построить группу, изоморфную дилатациям, исходя из найденного вида генератора. Эта группа имеет вид
изоморфна g, однако, вообще говоря, с ней не совпадает. Таким образом, легко построить группу, изоморфную дилатациям, исходя из найденного вида генератора. Эта группа имеет вид  . Однако, такое и им аналогичные построения следует воспринимать скорее как интерпретацию выражения
. Однако, такое и им аналогичные построения следует воспринимать скорее как интерпретацию выражения  в терминах действий, осуществляемых элементами исходной группы. При этом следует иметь в виду, что, если f, d - коммутирующие элементы алгебры Ли, то
в терминах действий, осуществляемых элементами исходной группы. При этом следует иметь в виду, что, если f, d - коммутирующие элементы алгебры Ли, то  . В иных случаях,
. В иных случаях,  , где s должно быть специальным образом вычислено. Сама процедура такого вычисления устанавливается формулой Кэмпбела – Бейкера - Хаусдорфа (КБХ) (Р. Рихтмайер/Принципы современной математической физики. – М.: Мир, 1984. – 169с.) Она представляет собой ряд, первые несколько членов которого таковы:
, где s должно быть специальным образом вычислено. Сама процедура такого вычисления устанавливается формулой Кэмпбела – Бейкера - Хаусдорфа (КБХ) (Р. Рихтмайер/Принципы современной математической физики. – М.: Мир, 1984. – 169с.) Она представляет собой ряд, первые несколько членов которого таковы:

Приведем таблицу наиболее распространенных однопараметрических преобразований на плоскости и им соответствующих генераторов алгебры Ли.
Таблица 1 Преобразования на плоскости.
| Название | Формула | Генератор |
Перенос вдоль оси 
| 
| 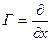
|
Перенос вдоль прямой

| 
| 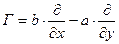
|
| Вращение | 
| 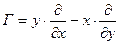
|
| Преобразование Лоренца | 
| 
|
| Преобразование Галилея | 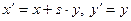
| 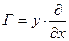
|
| Однородное растяжение | 
| 
|
| Неоднородное растяжение | 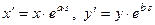
| 
|
Описанная точка зрения является конструктивной в том отношении, что для некоторых типов эволюционных уравнений позволяет явно построить процедуры их решения как процедуры трансформации начальных или краевых условий элементами некоторой группы. Сама эта группа находится по генераторам алгебры Ли, входящим в соответствующее эволюционное уравнение и может быть проинтерпретирована в терминах движений. Может так оказаться, и оказывается, в частности, при моделировании эволюции структур (см. гл. 6), что моделировать эти движения проще, чем сеточными или иными приемами решать соответствующие уравнения.
Рассмотрим подробнее эти вопросы.
При рассмотрении целого ряда различных по природе физических полей возникают сходные по структуре уравнения, описывающие их поведение. Это эволюционные уравнения. Так, например, при рассмотрении процессов переноса излучения, течения жидкости в пористых средах, изотермического течения идеального газа, процессов теплообмена, течения слабо сжимаемой жидкости, уравнения движения вязкой среды и многие другие (см. гл.2) возникают уравнения эволюционного типа.
Они имеют вид:
 , (9)
, (9)
где  - пространственные координаты,
- пространственные координаты,  - эволюционирующая во времени величина. Она может быть скаляром или вектором, иметь и более сложную природу.
- эволюционирующая во времени величина. Она может быть скаляром или вектором, иметь и более сложную природу.  - некоторое преобразование, называемое эволюционным преобразованием и
- некоторое преобразование, называемое эволюционным преобразованием и 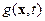 - распределение внешних источников. Уравнение (9) должно быть дополнено начальным условием
- распределение внешних источников. Уравнение (9) должно быть дополнено начальным условием  , совместно с которым и рассмотрено.
, совместно с которым и рассмотрено.
Уравнения типа (9) являются обобщением уравнений, описывающих процесс поглощения энергии или другой характеристики некоторого излучения, в процессе его распространения, эволюции в некоторой поглощающей среде.
Рассмотрим некоторые простые частные случаи.
Пусть в среде распространяется вдоль некоторой линии  излучение, энергия которого описывается функцией
излучение, энергия которого описывается функцией 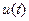 , где t – параметр вдоль линии, однозначно характеризующий ее точку. Например, линия
, где t – параметр вдоль линии, однозначно характеризующий ее точку. Например, линия  может совпадать с осью
может совпадать с осью  , а параметром
, а параметром 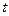 служит координата x на этой прямой. Выбрав элементарный интервал
служит координата x на этой прямой. Выбрав элементарный интервал  вдоль кривой
вдоль кривой  , и рассмотрев механизм поглощения энергии при его прохождении, приходим к выводу о том, что относительное изменение энергии на этом интервале пропорционально величине этого интервала с коэффициентом пропорциональности А, который называется коэффициентом поглощенияи служит эволюционным оператором:
, и рассмотрев механизм поглощения энергии при его прохождении, приходим к выводу о том, что относительное изменение энергии на этом интервале пропорционально величине этого интервала с коэффициентом пропорциональности А, который называется коэффициентом поглощенияи служит эволюционным оператором:

Знак минус в правой части указывает на поглощение энергии. Таким образом, приходим к дифференциальному уравнению:
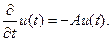 (10)
(10)
Это пример уравнения (9). Имея начальные условия:  решение этого уравнения можно представить в виде:
решение этого уравнения можно представить в виде:
 (11)
(11)
Усложним задачу. В том случае, когда коэффициент поглощения, он же эволюционный оператор, является функцией координат, можно считать, что он меняется вдоль параметра t, и уравнение поглощения будет иметь вид:
 (12)
(12)
Это новая модификация уравнения (9). Его решение при тех же начальных данных имеет вид:
 . (13)
. (13)
В частности, решение уравнения (12) в форме (13) составляет предмет рассмотрений в компьютерной томографии, при решении, например, задач рентгеновской диагностики.
Действительно, если изучается распределение в области V пространства коэффициента поглощения 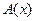 , то с каждой парой точек
, то с каждой парой точек 
 на поверхности объема V можно связать линию
на поверхности объема V можно связать линию  , вдоль которой происходило распространение и поглощение сигнала. Тогда из (13) имеем:
, вдоль которой происходило распространение и поглощение сигнала. Тогда из (13) имеем:
 , откуда
, откуда
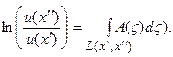
Левая часть этого уравнения – известная, измеренная на границе области V функция двух переменных – источника и приемника излучения. Решение этого интегрального уравнения позволяет восстановить распределение коэффициента поглощения вдоль линии  , увидеть «срез» по этой линии коэффициента поглощения. Имея достаточное число таких срезов, можно ставить задачу восстановления распределения в пространстве коэффициента поглощения (см. гл.2).
, увидеть «срез» по этой линии коэффициента поглощения. Имея достаточное число таких срезов, можно ставить задачу восстановления распределения в пространстве коэффициента поглощения (см. гл.2).
Наконец, следующее усложнение. Уравнение со стационарным (не зависящем от времени) эволюционным оператором (коэффициентом поглощения), но с присутствующими и меняющимися во времени внешним источниками 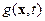 :
:
 (14)
(14)


