 |
Главная |
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 13
|
из
5.00
|
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 13
По дисциплине: ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ
Наименование работы: ВЫЧИСЛЕНИЕ ДВОЙНЫХ ИНТЕГРАЛОВ
С ПОМОЩЬЮ ПОЛЯРНЫХ КООРДИНАТ.
Для специальности 230111, 230115.
Составлено преподавателем Калмыковой О.И.
г. Смоленск
2012 г.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 13
По дисциплине: ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ (2 курс)
Наименование работы: ВЫЧИСЛЕНИЕ ДВОЙНЫХ ИНТЕГРАЛОВ
С ПОМОЩЬЮ ПОЛЯРНЫХ КООРДИНАТ.
1. Цель работы:Приобретение навыков вычисления двойного интеграла в полярных координатах, перехода от прямоугольных координат х и y к полярным  и φ.
и φ.
2. Литература:
2.1. Богомолов Н.В. "Практические занятия по математике" гл.29 §4 М.: Высшая школа, 1990 г.
3. Подготовка к работе:
3.1. Изучить теоретический материал по теме “Вычисление двойных интегралов с помощью полярных координат ”.
3.2. Подготовить бланки отчета.
3.3. Подготовить ответы на вопросы допуска к работе:
3.3.1. Понятие функции двух переменных. Область определения функции двух переменных.
3.3.2. Понятие двойного интеграла.
3.3.3. Формула преобразования двойного интеграла от прямоугольных координат х и y к полярным ρ и φ.
3.3.4. Правило изменения порядка интегрирования в двойном интеграле.
4. Основное оборудование:
4.1. Литература, конспект.
5. Задание:
5.1. Перейти в двойном интеграле к полярным координатам и расставить пределы интегрирования.
5.2. Вычислить с помощью перехода к полярным координатам двойной интеграл по указанной области.
6. Порядок выполнения работы:
6.1. Записать задание своего варианта в отчет.
6.2. Выполнить вычисление двойного интеграла с помощью полярных координат.
6.3. Записать ответы, оформить отчет
6.4. Подготовить ответы на контрольные вопросы.
7. Содержание отчета:
7.1. Титульный лист.
7.2. Цель работы.
7.3. Результаты и ход выполнения работы.
7.4. Выводы, ответы.
8. Контрольные вопросы:
8.1. Понятие функции двух переменных. Область определения функции двух переменных.
8.2. Понятие двойного интеграла.
8.3. Формула преобразования двойного интеграла от прямоугольных координат х и y к полярным ρ и φ.
8.4. Правило изменения порядка интегрирования в двойном интеграле.
9. Приложение:
| Вариант 1. | Вариант 2. |
1).  D – круг D – круг  2).
2). 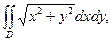 D –1 четверть круга D –1 четверть круга 
| 1).  D – полукруг D – полукруг 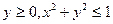 2).
2).  D – круговой сектор D – круговой сектор
  , , 
|
| Вариант 3. | Вариант 4. |
1).  D – круговой сектор D – круговой сектор  2).
2).  D – круговое кольцо D – круговое кольцо 
| 1).  D – круговое кольцо D – круговое кольцо 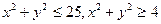 2).
2).  D – полукруг D – полукруг 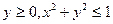
|
| Вариант 5. | Вариант 6. |
1).  D – круговое кольцо D – круговое кольцо  2).
2).  D – круг D – круг 
| 1).  D – круг D – круг 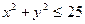 2).
2).  D – круговой сектор D – круговой сектор  
|
| Вариант 7. | Вариант 8. |
1).  D – полукруг D – полукруг  , ,  2).
2).  , D – круг , D – круг 
| 1).  D – круговой сектор D – круговой сектор 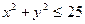 , ,  , ,  2).
2). 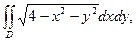 D – кольцо D – кольцо  , , 
|
10. Методические указания.
ДВОЙНОЙ ИНТЕГРАЛ В ПОЛЯРНЫХ КООРДИНАТАХ.
Формула преобразования двойного интеграла от декартовых координат x и y к полярным координатам ρ и ψ, связанным с декартовыми соотношениями
X= ρ cos φ, y= ρ sin φ,
Имеет вид
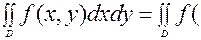 ∫D∫f(ρcosφ,ρsinφ) ρ d p dφ, (1)
∫D∫f(ρcosφ,ρsinφ) ρ d p dφ, (1)
Где ρ и φ – полярные координаты точек области D.
Вычисление двойного интеграла в полярных координатах сводится к вычислению повторных интегралов по ρ и по φ в зависимости от характера области D.




 ρ = ρ2(φ)
ρ = ρ2(φ)
 |
D
 |
ρ = ρ1(φ)
0 ρ= ρ(φ)
1.Если область D ограничена лучами, образующими с полярной осью углы φ1 и φ2, и кривыми ρ= ρ1(φ) и ρ= ρ2(φ) ( где φ1< φ2, ρ1< ρ2), то
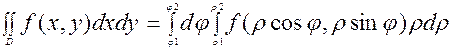 (2)
(2)
2. Если область D ограничена линией ρ= ρ(φ) и начало координат лежит внутри области, то
 (3)
(3)
Если же область интегрирования не удовлетворяет указанным условиям, то для вычислений двойного интеграла с помощью однократных интегрирований по ρ и по φ надо предварительно разбить область на части, обладающие отмеченными выше свойствами.
Пример:
Вычислить двойной интеграл

где область D – кольцо, ограниченное окружностями x2 +у2 =1, х2+у2=4.
Решение. Уравнения окружностей х2+у2=1 и х2+у2=4 в полярных координатах соответственно имеют вид ρ=1 и ρ=2, причем полярный угол φ изменяется в пределах от 0 до 2π; подынтегральная функция √4 – х2 – у2 в полярных координатах запишется в виде √4 – ρ2 . Следовательно, по формуле (1) имеем

(так как интегралы, составляющие двукратный интеграл, не зависят друг от друга, то последний равен произведению этих интегралов).
|
из
5.00
|
Обсуждение в статье: ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 13 |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

