Вывести формулу сферического избытка треугольника, используя формулу Лежандра

В каких случаях в триангуляционной сети возникает геометрическое условие координат. Привести примеры.

Для того чтобы при создании геодезической сети можно было вычислить на плоскости координаты всех вновь определяемых пунктов, должны быть известны координаты исходного пункта, длина и азимут исходной стороны, а также необходимое число измеренных углов или длин сторон треугольников (в каждом треугольнике по два угла или по две стороны). В этом случае координаты пунктов определяются однозначно, но бесконтрольно, подчас с большими ошибками. При этом не будет возможности ни выявить, ни устранить эти ошибки, а также оценить точность тех или иных элементов сети. Для устранения этих недостатков и повышения точности построения сети, в ней выполняют в достаточно большом объеме так называемые избыточные измерения горизонтальных углов, длин сторон, азимутов сторон и т. п.

При вставке сети более низкого класса в сеть более высокого класса кроме избыточно измеренных углов, длин сторон и т. п. появляются еще и избыточные исходные данные, не подлежащие изменениям при уравнивании вставляемой сети. К ним относятся координаты пунктов, длины и дирекционные углы сторон сети более высокого класса.

При наличии в геодезической сети как избыточно измеренных величин, так и избыточных исходных данных возникает необходимость уравнивания сети за возникающие в ней геометрические условия.

Условные уравнения координат (абсцисс и ординат) возникают только в том случае, если в сети триангуляции имеются раздельные группы исходных (жестких) пунктов, удаленные одна от другой не менее чем на две определяемые стороны. Отдельная группа исходных пунктов может состоять либо из одного такого пункта, либо из нескольких смежных пунктов. Например в одну группу исходных пунктов входят два смежных пункта А и В, а в другую, удаленную от первой на две определяемые стороны ВС и CD — один исходный пункт D (рис. 1).

 

Рис. 1 Цепочка треугольников между тремя исходными пунктами и измеренной

стороной и азимутом.

При составлении условий координат в сети выделяют цепочку треугольников, соединяющую ближайшие пункты разных групп исходных пунктов, и в ней намечают ходовую линию, проходящую через вершины промежуточных углов треугольников.

 

В уравненной сети должны соблюдаться равенства:

D D

XD = XB + ∑∆x; yD = yB + ∑∆y;

B B

 

где ∆х' и ∆у' — приращения координат, вычисленные с использованием измеренных углов А', В', С в треугольниках; (∆х), (∆у) — поправки в их значения из уравнивания сети.

Для получения условий координат в окончательном виде поправки (∆х) и (∆у) в приращения координат следует выразить через поправки (A), (В), (С)в измеренные углы в треугольниках. Выполнив эти преобразования, получим для случая уравнивания триангуляции по углам:

условное уравнение абсцисс

 

∑ (хn - х) ctg А ' ( А ) - ∑ (хn - х) ctg В ' ( В ) - ∑ (yn - y) (± С) + 206,265ὼX = 0;

 

Условное уравнение ординат

 

∑ (yn - y) ctg А ' ( А ) - ∑ (yn - y) ctg В ' ( В ) - ∑ (xn - x) (± С) + 206,265ὼy = 0;

 

где

ὼX = хn ' – хn ; ὼy = yn ' – yn ;

 

 

В этих уравнениях: (хп—х) и (уп—у) — разности координат (в км) последнего пункта D ходовой линии и координат текущих пунктов ходовой линии, включая исходный пункт В в начале этой линии; (А) и (В) — поправки в связующие углы A и В в треугольниках, при этом измеренный угол В лежит против исходной, а угол A— против определяемой в треугольнике стороны; (С)—поправки в промежуточные углы С, при этом поправка (С) имеет знак плюс ( + С), если угол С расположен слева от ходовой линии, и знаком минус (—С), если справа от нее, идя от начального пункта В этой линии к конечному пункту D .

Свободные члены ὼX и ὼy(в м) находят по формулам как разности вычисленных по измеренным углам координат хn ', yn ' и заданных координат x,yконечного пункта D ходовой линии.

При уравнивании триангуляции по направлениям поправки в углы выражают через поправки в измеренные направления.

 

 

Вывести формулу сферического избытка треугольника, используя формулу Лежандра.

После того как получены окончательные значения измеренных направлений или углов на поверхности эллипсоида, переходят к решению треугольников. Задача заключается в последовательном вычислении длин сторон треугольников триангуляции, причем известны одна сторона и углы в каждом треугольнике.

Строго говоря, треугольники триангуляции являются сфероидическими или эллипсоидальными треугольниками, поскольку они образованы на поверхности эллипсоида. На практике обычно приходится иметь дело с треугольниками, стороны которых не превышают 40-50 км и в редких случаях достигают 70-80 км. Вследствие близости земного эллипсоида к сфере различие в элементах сфероидических и сферических треугольников триангуляции пренебрегаемо. Таким образом, вычисление треугольников триангуляции сводится к решению сферических треугольников. Если решать треугольники по обычным формулам сферической тригонометрии, то стороны необходимо выражать в частях радиуса, но это неудобно, так как практически стороны должны быть выражены в метрах. Поэтому треугольники триангуляции решают особыми методами, пользуясь теоремой Лежандра или способом аддитаментов.

В сферическом треугольнике сумма углов больше 180° на величину, называемую сферическим избытком (ɛ).

Пусть АВС – сферический треугольник, стороны которого в линейных единицах обозначим через a,b,с. По сторонам a,b,c построим плоский треугольник А1,В1,С1, углы сферического треугольника обозначим соответственно через А,В,С, а углы плоского - через А1,В1,С1

 

 

Искомые значения углов плоского треугольника в окончательном виде выразятся простыми формулами: А1 = А - ɛ/3, В1 = В - ɛ/3, С1 = С - ɛ/3, где ɛ - сферический избыток треугольника. Эти формулы выражают теорему Лежандра для малых треугольников.

Поставим задачу найти разности углов А-А1, В-В1,С-С1. Зная эти разности, можем от сферических треугольников переходить к плоским, имеющим такие же значения длин сторон, и таким образом, производить решение треугольников, применяя формулы прямолинейной тригонометрии.

Обозначим через R радиус шара, на котором построен сферический треугольник. Тогда, применив формулу косинуса стороны для сферического треугольника АВС, напишем:

Откуда

 

 

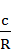Пренебрегая пятыми степенями малых величин , и формулу переписываем в виде

 

 

 

С принятой точностью имеем

 

 

или

 

 

После перемножения т приведения подобных членов получим:

 

Для плоского треугольника А1В1С1 имеем

 

 

Откуда

и

 

 

 

Принимая во внимание выражения (2) и (3), преписываем формулу (1)

 

 

Или

 

 

 

Разность – малая величина, поэтому можно положить:

 

 

На этом основании получаем

 

Площадь P треугольника может быть выражена формулой

Поэтому

 

Аналогично предыдущему

 

 

 

Складывая почленно три последних уравнения и принимая во внимание, что

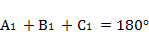, получаем

 

 

Так как сумма углов сферического треугольника равна 180º + , где – сферический избыток треугольника, то

 

 

Задача 1